Practicing the CBSE Sample Papers for Class 10 Maths Standard Set 5 allows you to get rid of exam fear and be confident to appear for the exam.
CBSE Sample Papers for Class 10 Maths Standard Set 5 with Solutions
Section – A
Question 1.
What will be the total surface area of a cube whose diagonal is 5√3 cm?
(a) 155 cm2
(b) 150 cm2
(c) 149 cm2
(d) 152 cm2
Answer:
(b) 150 cm2
ExPlanatiion: Diagonal of cube = 5√3
a√3 = 5√3 Where a is the side of cube.
a = 5 cm
Total surface area of cube = 6a2
= 6 × (5)2
= 6 × 25
= 150 cm2
![]()
Question 2.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°, respectively. If the bridge is at a height of 9 m from the surface of river, then find the width of the river:
(a) 23 m
(b) 25 m
(c) 27 m
(d) 29 m
Answer:
(b) 25 m
Explanation: Here, width of the river = DC
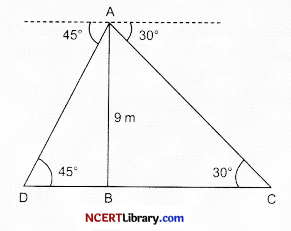
In △ABC,
tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ BC = \(\frac{9}{\tan 30^{\circ}}\) = 9√3 m
Now, in △ABD
tan 45° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ 1 = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ AB = BD
⇒ BD = 9 m
Hence, DC = DB + BC = 9 + 9√3
= 9(√3 + 1) [√3 = 1.732]
= 9(1.732 + 1)
= 9 × 2.732
= 24.588 m
– 25 m.
Question 3.
The tops of two poles of height 24 m and 36 m are connected by a wire. If the wire makes an angle of 60° with the horizontal, then the length of the wire is:
(a) 8√3 m
(b) 8 m
(c) 6√3 m
(d) \(\frac{8}{\sqrt{3}} \mathrm{~m}\)
Answer:
(a) 8√3 m
Explanation: Let AB and DC be two poles and AD be the wire
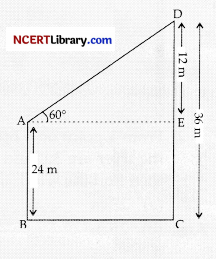
In △ADE,
sin 60° = \(\frac{\mathrm{DE}}{\mathrm{AD}}\) [AD = Length of wire]
⇒ AD = \(\frac{\mathrm{DE}}{\mathrm{sin 60° }}\) = \(\frac{\frac{12}{\sqrt{3}}}{2}\)
= \(\frac{12 \times 2}{\sqrt{3}}\) = \(\frac{24 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}\)
[On multiplying and dividing by √3 ]
= \(\frac{24 \sqrt{3}}{3}\) = 8√3 m
Question 4.
In the given fig., two line segments, AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then ∠PBA is equal to:
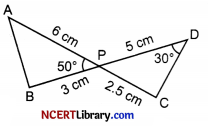
(a) 30°
(b) 60°
(c) 80°
(d) 100°
Answer:
(d) 100°
Explanation: Given, ABC is a isosceles triangle.
In △APB and △CPD, ∠APB = ∠CPD = 50° [vertically opposite angles]
\(\frac{\mathrm{AP}}{\mathrm{PD}}\) = \(\frac { 6 }{ 5 }\) ….(i)
and \(\frac{\mathrm{BP}}{\mathrm{CP}}\) = \(\frac { 3 }{ 2.5 }\) = \(\frac { 6 }{ 5 }\) …(ii)
From equatons (i) and (ii),
\(\frac{\mathrm{AP}}{\mathrm{PD}}\) = \(\frac{\mathrm{BP}}{\mathrm{CP}}\)
.’. △APB ~ △DPC [by SAS similarity criterion]
.’. ∠A = ∠D = 30° [corresponding angles of similar triangles]
In △APB, ∠A + ∠B + ∠APB = 180° [sum of angles of a triangle = 180°]
⇒ 30° + ∠B + 50° = 180°
.’. ∠B = 180° – (50° + 30°)
= 100°
i.e., ∠PBA = 100°.
Question 5.
If the point P(k, 0) divides the line segment joining the points A(2, – 2) and B(- 7, 4) in the ratio 1 : 2, then the value of k is:
(a) 1
(b) 2
(c) – 2
(d) – 1
Answer:
(d) – 1
Explanation: By section formula,
x = \(\frac{m x_2+n x_1}{m+n}\)
y = \(\frac{m y_2+n y_1}{m+n}\)

Here x = k, m = 1, n = 2, x1 = 2, x2 = – 7
.’. We get, k = \(\frac{(1)(-7)+(2)(2)}{1+2}\)
⇒ k = \(\frac{-7+4}{3}\)
⇒ k = \(\frac{-3}{3}\)
⇒ k = – 1
Question 6.
A solid right-circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is:
(a) 1 : 2
(b) 1 : 4
(c) 1 : 6
(d) 1 : 8
Answer:
(d) 1:8 cm
Explanation: Let the height of the bigger cone be 2x cm.
Thus, height of the smaller cone = x cm
Also let the radius of the larger cone be 2r cm.
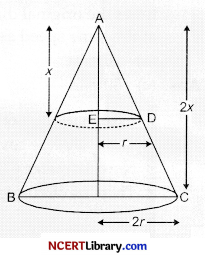
Thus, radius of the smaller cone = r cm (by mid-point theorem)
Now, volume of the large cone
V = \(\frac{1}{3}\) × π(2r)2 (2x) = \(\frac{8π}{3}\)r2x
and volume of the smaller cone
= \(\frac{1}{3}\)π(r2) (x)
= \(\frac{π}{3}\)r2x
Thus, \(\frac{Volume of the smaller cone}{Volume of the larger cone}\) = \(\frac{\frac{\pi}{3} r^2 x}{\frac{8 \pi}{3} r^2 x}\) = \(\frac{1}{8}\)
Question 7.
A man on the top of a vertical tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this, will the car reach the tower?
(a) 16.39 min
(b) 15.55 min
(c) 16.54 min
(d) 16.20 min
Answer:
(a) 16.39 in
ExPlanation:
Let h be the height of vertical tower. Time taken by car to reach point A to B is 12 min.
Let v be the velocity of car.
AB = distance travelled by car in 12 min.
So, AB = 12 v
Suppose, the car takes t minutes to reach from B to C
Then BC = vt
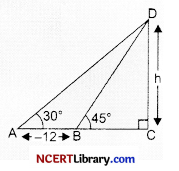
In △BCD, we have tan 45° = \(\frac{\mathrm{DC}}{\mathrm{BC}}\)
⇒ 1 = \(\frac{h}{vt}\)
h = vt …(i)
In △ACD, we have tan 30° = \(\frac{\mathrm{DC}}{\mathrm{AC}}\)
\(\frac{1}{√3}\) = \(\frac{h}{12 v+v t}\) ….(ii)
From (i) and (ii), we get √3vt = 12 v + vt
√3t = t + 12
t (√3 – 1) = 12
t = \(\frac{12}{√3 – 1}\) = 16.39 min or 16 min 23 sec.
Question 8.
A can go around a circular path 8 times in 40 minutes. If the diameter of the circle is increased to 10 times the original diameter, then the time required by A to go around the new path once, travelling at the same speed as before is:
(a) 20 min
(b) 25 min
(c) 50 min
(d) 100 min
Answer:
(c) 50 min
Explanation: Let original diameter be d metres. Then, its circumference = (πd) metres
Time taken to cover (8πd) m = 40 min
New diameter = (10 d) m.
Then, its circumference = (π × 10d) m
∴ Time taken to go around it once = \(\left(\frac{40}{8 \pi d} \times 10 \pi d\right)\)m = 50 min
Question 9.
What are the two consecutive even integers whose square have sum 340?
(a) 14 and 16
(b) 12 and 14
(c) 13 and – 12
(d) – 12 and 16
Answer:
(b) 12 and 14
Explanation: Let x and (x + 2) be two consecutive even integers.
x2 + (x + 1)2 =340
⇒ x2 + x2 + 4x + 4 = 340
⇒ 2x2 + 4x + 4 =340
⇒ x2 + 2x + 2 = 170
⇒ x2 + 2x – 168 = 0
⇒ x2 + 14x – 12x -168 = 0
⇒ x(x + 14) – 12 (x + 14) =0
⇒ (x – 12) (x + 14) =0
⇒ x = 12 or x = – 14
So, given number can be 12,14 or – 12, -14.
Question 10.
Find the roots of the quadratic equation 2x2 + x – 1 = 0:
(a) – 1 and \(\frac { 1 }{ 2 }\)
(b) 1 and – \(\frac { 1 }{ 2 }\)
(c) 2 and \(\frac { 1 }{ 2 }\)
(d) 1 and 2
Answer:
(a) – 1 and \(\frac { 1 }{ 2 }\)
ExPlanatiion: Given, 2x2 + x – 1 = 0
⇒ 2x2 + 2x – x – 1 = 0
⇒ 2x (x + 1) – 1 (x + 1) = 0
⇒ (x + 1) – 1 (2x – 1) = 0
⇒ x = – 1 or x = \(\frac { 1 }{ 2 }\)
Hence roots of equation are – 1 and \(\frac { 1 }{ 2 }\).
![]()
Question 11.
In a right angled triangle, if tan θ = \(\frac { 3 }{ 4 }\), then what is the length of greatest side of the triangle?
(a) 6 units
(b) 10 units
(c) 7 units
(d) 5 units
Answer:
(d) 5 units
Explanation: Given, tan θ = \(\frac { 3 }{ 4 }\)
Length of greatest side = Hypotenuse of triangle
As, tan θ = \(\frac { Perpendicular }{ Base }\) = \(\frac { 3 }{ 4 }\)
Let, P = 3 and B = 4.
By Pythagoras theorem, H2 = P2 + B2
⇒ H2 = (3)2 + (4)2
⇒ H2 = 9 + 16
⇒ H2 = 25
⇒ H = 5
Hence length of greatest side is 5 units.
Question 12.
What is the mean of the following data?
| Class interval | Frequency |
| 50-60 | 8 |
| 60-70 | 6 |
| 70-80 | 12 |
| 80-90 | 11 |
| 90-100 | 13 |
(a) 78
(b) 68
(c) 48
(d) 58
Answer:
(a) 78
Explanation:
| Class Interval | f | x | f × x |
| 50-60 | 8 | 55 | 440 |
| 60-70 | 6 | 65 | 390 |
| 70-80 | 12 | 75 | 900 |
| 80-90 | 11 | 85 | 935 |
| 90-100 | 13 | 95 | 1235 |
| Σf = 50 | Σfi xi = 3900 |
Question 13.
13. How many multiples of 4 are there in between 10 and 250?
(a) 70
(b) 60
(c) 65
(d) 73
Answer:
(b) 60
Explanation: Between 10 and 250 multiples of 4 are
12,16,20,………….., 248
The given numbers are in A.P.
So, a = 12, d = 4
an = 248
Let the number of terms = n ∵ an = a + (n – 1)d
∴ 248 = 12 + (n – 1)4
⇒ 236 = 4n – 4
⇒ 236 = 4n
⇒ n = \(\frac { 240 }{ 4 }\) = 60
Hence, there are 60 multiples of 4 between 10 and 250.
Question 14.
If cosec θ – cot θ = \(\frac { 1 }{ 3 }\), then find the value of cosec θ + cot θ:
(a) 3
(b) – 3
(c) 1
(d) None of these
Answer:
Explanation: Given, cosec θ – cot θ = \(\frac { 1 }{ 3 }\)
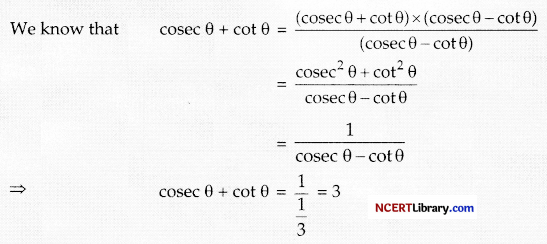
Question 15.
What will be the product of a non-zero rational number and an irrational number?
(a) rational number
(b) irrational number
(c) Integer number
(d) natural number.
Answer:
(b) irrational number.
Explanation: The product of a non-zero rational number and an irrational number is always irrational number.
Question 16.
If a pair of linear equations is consistent, then the lines will be:
(a) parallel
(b) always coincident
(c) intersecting or coincident
(d) always intersecting
Answer:
(c) intersecting or coincident
Explanation: If a pair of linear equations in two variables is consistent, then the lines represented by two equations are intersecting or coincident, i.e., either it has a unique solution or infinitely many solutions.
Question 17.
If a and p are the zeroes of a polynomial such that α + β = – 6 and αβ = – 4, then write the polynomial:
(a) x2 – 6x – 4 = 0
(b) x2 + 6x – 4 = 0
(C) x2 + 6X + 4 = 0
(d) x2 – 6x + 4 = 0
Answer:
(b) x2 + 6x – 4 = 0
Explanation: Given, α + β = – 6
and αβ = – 4
∴ The quadratic polynomial whose zeroes are α and β is given by
f(x) = x2 – (α + β)x + αβ.
∴ The polynomial is f(x) = x2 + 6x – 4 = 0
Question 18.
The system of equations 3x + y – 4 = 0 and 6x + 2y – 8 = 0 has :
(a) a unique solution x = 1, y = 1
(b) a unique solution x = 0, y = 4
(c) no solution
(d) infinite solution
Answer:
(d) infinite solution
Explanation: Given equation of system
3x+ y = 4
and 6x + 2y =8
Here, \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\) = \(\frac { 1 }{ 2 }\)
Therefore, the system of equation has infinite solutions because it is a coincident line.
Question 19.
DIRECTION: In the question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R).
Choose the correct option
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A)
(b) Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A)
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Statement A (Assertion): If the sum of n terms of a series is In2 + 3n + 1, then series is in A.P. with common difference 4.
Statement R (Reason): If sum of n terms of an A.P. is quadratic expression, then common difference is twice of the coefficient of quadratic term.
Answer:
(a) Both the assertion and the reason are correct and reason is the correct explanation of the assertion.
Explanation: As per the reason statement,
Sum of n terms of A.P. is Sn = \(\frac{n}{2}\) [2A + (n – 1)D]
Where A = first term, D = common difference. Hence, the sum of n terms of an A.P. is always in the form of quadratic expression. Hence, it is proved that reason is true.
As per the assertion given, Sn = 2n2 + 3n + 1
tn = Sn – Sn – 1
= 2(n2 + 3n + 1) – [2(n – 1)2 + 3(n – 1) + 1]
= 2[n2 – (n – 1)2] + 3[n – n + 1]
= 2[2n – 1] + 3
= 4n + 1
D = tn+ 1 – tn = 4
So, both assertion and reason are correct and reason is correct explanation of assertion.
Question 20.
Statement A (Assertion): If f(x) is a quadratic expression such that f(1) + f(2) = 0. If – 1 is a root of f(x) = 0, then the other root is 8/5.
Statement R (Reason): If f(x) = ax2 + bx + c, then α + β = – \(\frac{b}{a}\) and αβ = \(\frac{c}{a}\)
Answer:
(b) Both the assertion and the Reason are correct but the reason is not the correct explanation of the assertion.
Explanation: Given, f(1)+f(2) = 0
Forf(x) = ax2 + bx + c, we have
a + b + c + 4 a + 2b + c = 0
⇒ 5a + 3b + 2 c = 0 …(1)
Since – 1 is a root of the equation
f(-1) = a – b + c = 0 ….(2)
By eliminating c and b in turn by solving equations (1) and (2), we have
\(\frac{-b}{a}\) = \(\frac{3}{5}\), \(\frac{c}{a}\) = \(\frac{-8}{5}\)
Since – 1 is one root, the other root is \(\frac{8}{5}\).
Section – B
Question 21.
The point which divides the line segment joining the points (7, – 6) and (3, 4) in ratio 1 : 2 internally lies in which quadrant?
Answer:
Let P(x, y) be the required point which lie on the line segment AB.
So, using section formula,
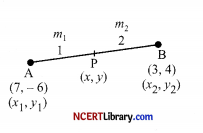
x = \(\frac{m_2 x_1+m_1 x_2}{m_1+m_2}\)
= \(\frac{2 \times 7+1 \times 3}{1+2}\)
= \(\frac{14 + 3}{3}\) = \(\frac{17}{3}\)
and y = \(\frac{m_2 y_1+m_1 y_2}{m_1+m_2}\)
= \(\frac{2 \times(-6)+1 \times 4}{1+2}\)
= \(\frac{-12+4}{3}\) = \(\frac{-8}{3}\)
Thus, point of P \(\left(\frac{17}{3}, \frac{-8}{3}\right)\) lies in the 4th quadrant.
![]()
Question 22.
Find the largest number which divides 70 and 125 leaving remainder 5 and 8 respectively.
OR
Express 23150 as product of its prime factors. Is it unique?
Answer:
It is given that on dividing 70 by the required number, there is a remainder 5. This means that 70 – 5 = 65 is exactly divisible by the required number.
Similarly, 125 – 8 = 117 is also exactly divisible by required number.
Now, required number = H.C.F. (65, 117)

∴ 65 = 5 × 13
and 117 = 32 × 13
∴ H.C.F. (65, 117) = 13
∴ Required number = 13
OR

Prime factors of 23150 = 2 × 5 × 5 × 463.
As per the fundamental theorem of Arithmetic, every number has a unique factorisation.
Question 23.
A number x is selected from the numbers 1, 2, 3 and then a second number y is randomly selected from the numbers 1,4,9. What is the probability that the product xy of the two numbers will be less than 9?
Answer:
Number ‘x’ is selected from {1, 2, 3}.
Number ‘y’ is selected from (1, 4, 9}.
Total number of outcomes = 9
Product of xy less than ‘9’ = {(1,1), (1, 4), (2,1), (2, 4), (3,1)}
∴ P(Product xy less than 9) = \(\frac { 5 }{ 9 }\)
Question 24.
For what value of k, the quadratic equation kx2 + 11x – 4 = 0 has real roots?
Answer:
Given quadratic equation is
kx2 + 11x – 4 = 0
On comparing with ax2 + bx – c = 0, we get
a = k, b = 11, c = – 4
∵ It has real roots.
∴ D ≥ 0
⇒ b2 – 4ac ≥ 0
⇒ (11)2 – 4 × k × (- 4) ≥ 0
⇒ 121 + 16k ≥ 0
⇒ k ≥ \(\frac { – 121 }{ 16 }\)
Question 25.
If the sum of n terms of an A.P. is S2 = 3n2 + 5n, then write its common difference.
OR
If the ratio of sum of the first m and n terms of an A.P. is m2 : n2, show that the ratio of its mth and nth terms is (2m – 1): (2n – 1).
Answer:
We have,
Sn = 3n2 + 5n
⇒ Sn – 1 = 3(n – 1)2 + 5(n – 1)
= 3(n2 + 1 – 2n) + 5n – 5
= 3n2 + 3 – 6n + 5n – 5 = 3n2 – n – 2
General term of A.P. is given as, Tn = Sn – Sn – 1
= 3n2 + 5n – 3n2 + n + 2
= 6n + 2
Putting n = 1, 2, 3, we get T1 = 6 × 1 + 2 = 8
T2 = 6 × 2 + 2 = 14
T3 = 6 × 3 + 2 = 20
Now, T2 – T1 = 14 – 8 = 6
and T3 – T2 = 20 – 14 = 6
∴ Common difference = 6
OR
Let Sm and Sn be the sum of the first m and n terms of the A.P., respectively.
Sn = \(\frac { m }{ 2 }\)[2a + (m – 1)d]
Sn = \(\frac { n }{ 2 }\)[2a + (n – 1)d]
Here, a is the first term and d is the common difference.
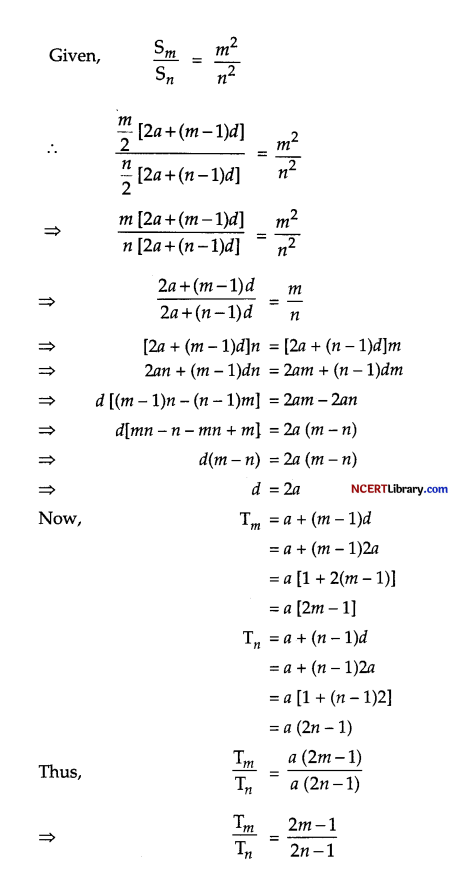
Section – C
Question 26.
Find the area of the quadrilateral ABCD whose vertices are A(- 4, – 2), B(- 3, – 5), C(3, – 2) and D(2,3).
Answer:
(Given, A = (- 4, – 2), B = (- 3, – 5), C = (3, – 2) and D – (2,3)
Area of ABCD = Area of △ABC + Area of △ADC
= \(\frac { 1 }{ 2 }\) | – 4(- 5 + 2) – 3(- 2 + 2) + 3(- 2 + 5) | + \(\frac { 1 }{ 2 }\) | – 4(3 + 2) + 2(- 2 + 2) + 3(- 2 – 3)
= \(\frac { 1 }{ 2 }\) | 12 + 0 + 9 | + \(\frac { 1 }{ 2 }\) | – 20 + 0 – 15 |
= \(\frac { 1 }{ 2 }\) | 21 | + \(\frac { 1 }{ 2 }\) | – 35 | = \(\frac { 21 }{ 2 }\) + \(\frac { 35 }{ 2 }\)
Question 27.
On a morning walk, three men step off together and their steps measure 54 cm, 60 cm and 48 cm, respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
Answer:
The minimum distance that each should walk is the LCM of 54, 60 and 48.
Now, 54 = 2 × 33
60 – 22 × 3 × 5
48 = 22 × 3
.’. LCM (54, 60,48) = 22 × 32 × 5
= 2160
.’. Required distance = 2160 cm
= 21 m 60 cm
Question 28.
A 5 m wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of ₹ 25 per m. [Use π = \(\frac { 22 }{ 7 }\)]
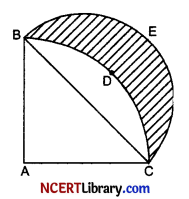
In the given figure, ABDC is a quadrant of a circle of radius 28 cm and a semi-circle BEC is drawn with BC as diameter. Find the area of the shaded region. [Use π = \(\frac { 22 }{ 7 }\)]
Answer:
Given, width of cloth = 5 m
Base diameter of tent = 14 m
.’. Radius = \(\frac { 14 }{ 2 }\) = 7 cm
Height = 24 m
Slant height of cone,
l = \(\sqrt{h^2+r^2}\)
= \(\sqrt{(24)^2+(7)^2}\)
= \(\sqrt{576+49}\)
= \(\sqrt{625}\)
= 25 cm
Let the length of the cloth be l’ m.
.’. Curved surface area of cone = Area of cloth
⇒ πrl = l’ × b
⇒ \(\frac { 22 }{ 7 }\) × 7 × 25 = l’ × 5
⇒ 22 × 25 = l × 5
⇒ l’ = \(\frac { 22 × 25}{ 5 }\) m
⇒ l’ = 110m
Thus, total cost of the cloth = ₹ (25 × 110) = ₹2750.
OR
Given: Radius = 28 cm
Thus, AB = AC = 28 cm
Now, Area of quadrant ABCD = \(\frac{\pi r^2}{4}\) = \(\frac{22}{7}\) × \(\frac{(28)^2}{4}\) = 616 cm2
Also, applying pythagoras’ theorem, we get
BC2 = AB2 + AC2
⇒ BC2 = (28)2 + (28)2
⇒ BC2 = 2(28)2
⇒ BC = 28√ 2 cm
Thus, radius of semi-circle BCE = 14√ 2 cm.
Hence, area of semi-circle BEC = \(\frac{\pi r^2}{2}\)
= \(\frac{22}{7}\) × \(\frac{(14 \sqrt{2})^2}{2}\)
= 616 cm2
and Area of △ABC = \(\frac { 1 }{ 2 }\) × 28 × 28 = 392 cm2
Thus, the area of the shaded region = Area of semi-circle BEC + Area of △ABC – Area of quadrant ABCD
= 616 cm2 + 392 cm2 – 616 cm2 = 392 cm2
Question 29.
In an A.P. the sum of first n terms is \(\frac{3 n^2}{2}\) + \(\frac{13 n}{2}\). Find the 25th term.
OR
Students of class X collected ? 18000. They wanted to divide it equally among a certain number of students residing in slums area. When they started distributing the amount, 20 more students from nearby slums also joined. Now each student got ₹ 240 less. Find the number of students living in the slum.
Answer:
Given, Sn = \(\frac{3 n^2+13 n}{2}\)
We know that, an = Sn – Sn – 1
Or a25 = S25 – S24
= \(\frac{3(25)^2+13(25)}{2}\) – \(\frac{3(24)^2+13(24)}{2}\)
= \(\frac { 1 }{ 2 }\) {3(252 – 242) + 13(25 – 24)}
= \(\frac { 1 }{ 2 }\) (3 × 49 + 13)
= \(\frac { 1 }{ 2 }\) × 160 = 80
OR
Let number of students living in slums area be x
∴ Share per student = ₹ \(\frac { 18000 }{ x }\)
When number of students = x + 20
Then, share per student = ₹ \(\frac { 18000 }{ x + 20 }\)
According to question,
\(\frac { 18000 }{ x }\) – \(\frac { 18000 }{ x + 20 }\) = 240
⇒ \(\frac{18000 x+360000-18000 x}{(x+20)(x)}\) = 240
⇒ 360000 = 240(x2 + 20 x)
⇒ 1500 =x2 + 20 x
⇒ x2+ 20 x – 1500 = 0
⇒ x2 + 50 x – 30 x – 1500 = 0
⇒ x(x + 50) – 30(x + 50) = 0
⇒ (x + 50)(x – 30) = 0
⇒ x = 30 or x = – 50 (Rejected)
⇒ x = 30
∴ Number of students living in the slum area = 30.
![]()
Question 30.
| Classes | 210 – 229 | 230 – 249 | 250 – 269 | 270 – 289 | 290 – 309 |
| Frequency | 8 | 9 | 10 | 7 | 2 |
Answer:
Given class interval is of inclusive form. We have to convert it to exclusive form by subtracting 0-5 from lower limit and adding 0.5 to upper limit of each class interval.
| Class interval | Corrected class interval | Frequency (fi) | Mid – value (xi) | ui(xi – A) | fi ui |
| 210 – 229 | 209.5 – 229.5 | 8 | 219.5 | -40 | 320 |
| 230 – 249 | 229.5 – 249.5 | 9 | 239.5 | -20 | -180 |
| 250 – 269 | 249.5 – 269.5 | 10 | 259.5 = A | 0 | 0 |
| 270 – 289 | 269.5 – 289.5 | 7 | 279.5 | 20 | 140 |
| 290 – 309 | 289.5 – 309.5 | 2 | 299.5 | 40 | 80 |
| Σ fi = 36 | Mid – value (xi) | Σ fi ui = -280 |
Mean = A + \(\frac{\Sigma f_i u_i}{\Sigma f_i}\)
= 259.5 + \(\frac { – 280 }{ 36 }\)
= 259.5 – 7.778
= 251.722
Question 31.
If tan θ + \(\frac { 1 }{ tan θ }\) = 2, find the value of tan2 θ + \(\frac{1}{\tan ^2 \theta}\)
Answer:
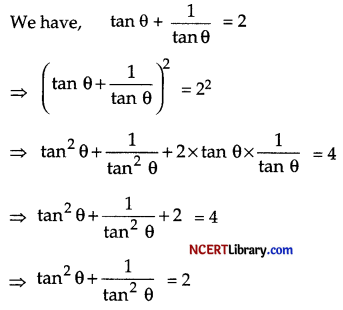
Section – D
Question 32.
(a) The third term of an A.P. is 7 and the seventh term exceeds three times the third term by 2. Find the first term, the common difference and the sum of first 20 terms.
(b) Find the sum of first seven numbers which are multiples of 2 as well as of 9.
Answer:
(a) Let a and d be the first term and common difference of given A.P. respectively.
Given: 3rd term of A.P. – 7
⇒ T3 = 7
⇒ a + 2d =7 …(i)
and T7 – 3T3 = 2
⇒ T7 – 3 × 7 = 2
⇒ T7 = 2 + 21
⇒ T7 = 23
⇒ a + 6d = 23 …….(ii)
Subtracting equation (ii) from (i), we get
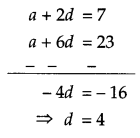
Putting the value of d in equation (i), we get
a + 2 × 4 = 7
⇒ a = 7 – 8 = – 1
Now, Sum of first 20 terms = \(\frac { 20 }{ 2 }\)[2a + (20 – 1)d]
= 10 [2 × (-1) + 19 × 4]
= 10 [-2 + 76]
= 10 × 74 = 740
(b) Numbers which are multiples of 2 and 9 are
18, 36, 54, 72, 90, 108, 126,……….
Since, 36 – 18 = 54 – 36 = 18
So, above series is an A.P. with a = 18, d = 18
Sum of first seven terms of the A.P. = \(\frac { 7 }{ 2 }\) [2a + (7 – 1 )d]
= \(\frac { 7 }{ 2 }\) [2 × 18 + 6 × 18]
= \(\frac { 7 }{ 2 }\) [36 + 108] = \(\frac { 7 }{ 2 }\) × 144
= 7 × 72 = 504
Question 33.
In the given figure, a disc is shown on which a player spins an arrow twice. The fraction \(\frac { a }{ b }\) is formed, where ‘a’ is the number of sector on which arrow stops on the first spin and ‘b’ is the number of the sector in which the arrow stops on second spin. On each spin, each sector has equal chance of selection by the arrow. Find the probability that the fraction \(\frac { a }{ b }\) > 1.
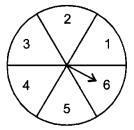
Answer:
Since the arrow can stop in any one of the six sectors. So, a and b both can assume values from 1 to 6.
Thus, the ordered pair (a, b) can assume the following values :
{(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2.1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3.1), (3,2), (3, 3), (3,4), (3,5), (3,6)
(4.1), (4,2), (4, 3), (4,4), (4,5), (4, 6)
(5.1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6.1), (6,2), (6,3), (6,4), (6,5), (6,6)}
Clearly, there are total 36 elementary events, out of which we have 6 elementary events (a, b) in the diagonal for which a – b and 15 elementary events (a, b) below the diagonal for which a>b.
∴ Favourable number of events = 15
Question 34.
In the figure, ∠BED = ∠BDE and E divides BC in the ratio 2 : 1. Prove that AF × BE = 2 AD × CF.
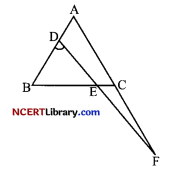
OR
The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac{\mathrm{AO}}{\mathrm{OC}}\) = \(\frac{\mathrm{BO}}{\mathrm{OD}}\). Show that ABCD is a trapezium.
Answer:
Since, E divides BC in the ratio 2 :1
∴ \(\frac{\mathrm{BE}}{\mathrm{EC}}\) = \(\frac { 2 }{ 1 }\)
∠BED =∠BDE [Given]
⇒ BD = BE …..(ii) [Sides opposite to equal angles]
In △CBG,
DE || CG [By construction]
⇒ \(\frac{\mathrm{BD}}{\mathrm{DG}}\) = \(\frac{\mathrm{BE}}{\mathrm{EC}}\) [Thale’s theorem]
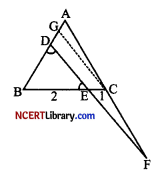
⇒ \(\frac{\mathrm{BD}}{\mathrm{DG}}\) = \(\frac{\mathrm{BE}}{\mathrm{EC}}\) = \(\frac { 2 }{ 1 }\) [From eq. (i)]
⇒ \(\frac{\mathrm{BD}}{\mathrm{DG}}\) = \(\frac { 2 }{ 1 }\)
⇒ 2DG = BD
⇒ 2DG = BE [From eq. (ii)]
⇒ DG = \(\frac { 1 }{ 2 }\)BE ….(iii)
In △ADF,
CG || DF [By construction]
⇒ \(\frac{\mathrm{AG}}{\mathrm{GD}}\) = \(\frac{\mathrm{AC}}{\mathrm{CF}}\) [Thalas’ theorem]
⇒ \(\frac{\mathrm{AG}}{\mathrm{GD}}\) + 1 = ⇒ \(\frac{\mathrm{AC}}{\mathrm{CF}}\) + 1 [Adding 1 on both sides]
⇒ \(\frac { AG + GD }{ GD }\) = \(\) = \(\frac { AC + CF }{ CF }\)
⇒ \(\frac{\mathrm{AD}}{\mathrm{GD}}\) = ⇒ \(\frac{\mathrm{AF}}{\mathrm{CF}}\)
⇒ AF × GD = AD × CF
⇒ AF × \(\frac { BE }{ 2 }\) = AD × CF [From ….(iii)]
⇒ AF × BE = 2AD × CF.
OR
Let EO || DC meet AD at E.
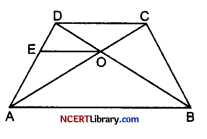
So, in △ADC, EO || DC
So, \(\frac{\mathrm{AO}}{\mathrm{OC}}\) = \(\frac{\mathrm{AE}}{\mathrm{ED}}\) [Thales’ theorem] …(i)
But \(\frac{\mathrm{AO}}{\mathrm{OC}}\) = \(\frac{\mathrm{BO}}{\mathrm{OD}}\) [Given] ….(ii)
By (i) and (ii),
So, \(\frac{\mathrm{BO}}{\mathrm{OD}}\) = \(\frac{\mathrm{AE}}{\mathrm{ED}}\)
Hence, \(\frac{\mathrm{BO}}{\mathrm{OD}}\) = \(\frac{\mathrm{AE}}{\mathrm{ED}}\) and BO, OD, AE and ED are segment of △DAB.
So, EO || AB [By converse of Thalas’ theorem]
But EO || DC
Thus, AB || DC
As there are only two parallel sides in this quadrilateral, it is a trapezium.
![]()
Question 35.
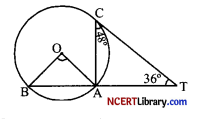
In the given figure, PQ is a chord of length 16 cm and the radius of the circle is 10 cm. The tangents at P and Q intersect at a Point T. Find the length of TP.
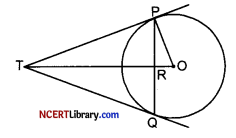
OR
A, B and C are three points on a circle. The tangent at C meets BA produced at T. Given that ∠ATC = 36° and that the ∠ACT = 48°, calculate the angle subtended by AB at the centre of the circle.
Answer:
Given, r = 10 cm and length of chord PQ = 16 cm.
As TO bisects PQ at R, so PR = RQ = 8 cm
Let TP = x cm and TR = y cm
Now OR2 = PO2 – PR2 [By pythagoras theorem as ∠PRO = 90°]
⇒ OR2 = (10)2 – (8)2
⇒ OR2 = 100 – 64
⇒ OR2 = 36
⇒ OR = 6cm
Thus, TO = TR + RO = (y + 6) cm
Also TP2 = TR2 + PR2
⇒ x2 = y2 + 82
⇒ x2 = y2 + 64 ……(i)
Again TO2 = OP2 + TP2
⇒ (y + 6)2 = 102 + x2
⇒ (y + 6)2 = 102 + y2 + 64 [From (i)]
⇒ y2 + 36 + 12y = y2 + 164
⇒ 36 + 12y = 164
⇒ 12y = 128
⇒ 3y = 32
⇒ y = \(\frac { 32 }{ 3 }\) cm
Hence TP2 = x2 = y2 + 64
⇒ TP2 = x2 = \(\left(\frac{32}{3}\right)^2\) + 64
⇒ x2 = \(\frac { 1024 }{ 9 }\) + 64
⇒ x2 = \(\frac { 1024 + 576 }{ 9 }\) = \(\frac { 1600 }{ 9 }\)
⇒ x = \(\frac { 40 }{ 3 }\)
Hence TP = 13.33 cm
OR
Let O be the centre of the circle. Join OC.
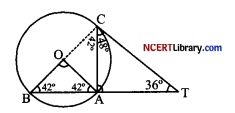
Since angle between the radius and the tangent is 90°.
∴ ∠OCT = 90°
⇒ ∠OCA = ∠OCT – ∠ACT
= 90° – 48° = 42°
and OA = OC = OB [Radii of the same circle]
⇒ ∠OAC = ∠OCA = 42° [Angles opposite to equal sides are equal]
In △ACT, exterior ∠CAB = ∠ACT + ∠CAT = 48° + 36° = 84°
∴ ∠OAB = ∠CAB – ∠OAC
⇒ ∠OAB = 84° – 42° = 42°
⇒ ∠OBA = ∠OAB = 42° [∵ OA = OB = rahjii]
In isosceles △AOB,
∠OBA + ∠OAB + ∠AOB = 180°
⇒ 42° + 42° + ∠AOB = 180°
⇒ ∠AOB = 180° – 84° = 96°
Hence, the angle subtended by AB at centre is 96°.
Section – E
Question 36.
The given picture shows the position of an aeroplane, at 2 points A and B flying horizontally at a uniform speed of 20 m/sec. It is found that it takes the aeroplane 10 minutes to fly from A to B. The angle of elevation of A and B from a point P on the ground are 30° and 60° respectively.
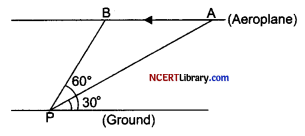
Answer the following questions :
(i) How much distance does the aeroplane travels in 10 minutes?
(ii) How high is the aeroplane flying from the ground?
OR
Find the distance of PB.
(iii) Find the distance of AP.
Answer:
(i) Distance covered = speed × time
= 20 × 10 × 60 m = 12,000 m = 12 km
(ii) Let the height of the aeroplane from the ground be ‘h’ km
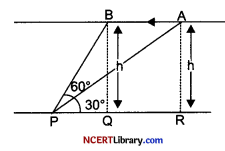
Question 37.
A child is playing with a rectangular sheet of paper. The dimensions of the paper is 25 cm × 14 cm. It can be rolled up along either side to form two cylinders A and B as shown
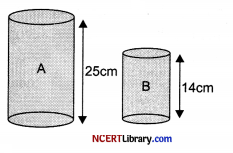
Answer the following questions :
(i) What is the volume of cylinder A?
OR
What is the volume of cylinder B?
(ii) Find the ratio of the radius of the cylinder A and B?
(iii) What is the formula of the curved surface area of the cylinder?
Answer:
(i) For cylinder A
h = 25 cm
and circumference of base, 2πr = 14 cm
⇒ \(\frac { 2 × 22 }{ 7 }\) r = 14
⇒ r = \(\frac { 7 × 14 }{ 44 }\) = \(\frac { 49 }{ 22 }\)
Then VA = πr2h
= \(\frac { 22 }{ 7 }\) × \(\frac { 49 }{ 22 }\) × \(\frac { 49 }{ 22 }\) × 25
= 389.8 cm3
OR
For cylinder B h’ = 14 cm
Circumference of base, 2πr’ = 25
r’ = \(\frac { 25 }{ 2π }\)
VB = πr’2h’
= \(\frac { π × 25 }{ 2π }\) × \(\frac { 25 }{ 2π }\) × 14
= \(\frac{625 \times 7 \times 7}{2 \times 22}\)
= 696.02 cm3
(ii) Radius of cylinder A, 2πr = 14
r = \(\frac { 14 }{ 2π }\) ….(i)
Radius of cylinder B, 2πr’ = 25
r’ = \(\frac { 25 }{ 2π }\) …..(ii)
From (i) and (ii), we get
\(\frac { r }{ r’ }\) = \(\frac{14 / 2 \pi}{25 / 2 \pi}\) = \(\frac { 14 }{ 25 }\)
(iii) 2πrh
Question 38.
Two hotels are at the ground level on either side of a mountain. On moving a certain distance towards the top of the mountain two huts are situated as shown in the figure. The ratio between the distance from hotel B to hut-2 and that of hut-2 to mountain top is 3 : 7.
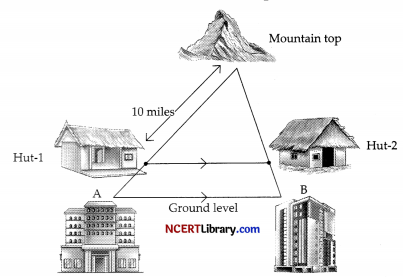
(i) What is the ratio of the perimeters of the triangle formed by both hotels and mountain top to the triangle formed by both huts and mountain top?
(ii) If distance between hut-1 and mountain top is 10 miles, then the distance between the hotel A and hut-1 is:
(iii) If the horizontal distance between the hut-1 and hut-2 is 8 miles, then the distance between the two hotels is:
OR
If the distance from mountain top to hut-1 is 5 miles more than that of distance from hotel B to mountain top, then what is the distance between hut-2 and mountain top?
Answer:
(i) Let AABC is the triangle formed by both hotels and mountain top. △CDE is the triangle formed by both huts and mountain top.
Clearly DE || AB and So △ABC ~ △DEC
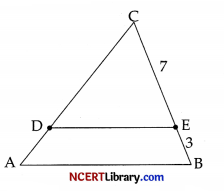
Now, required ratio = Ratio of their corresponding sides = \(\frac{\mathrm{BC}}{\mathrm{EC}}\) = \(\frac { 10 }{ 7 }\) i.e., 10 : 7.
(ii) Since, DE || AB, therefore
\(\frac{\mathrm{CD}}{\mathrm{AD}}\) = \(\frac{\mathrm{CE}}{\mathrm{EB}}\)
⇒ \(\frac { 10 }{ AD }\) = \(\frac { 7 }{ 3 }\)
⇒ AD = \(\frac{10 \times 3}{7}\) = 4.29 miles.
(iii) Since, △ABC ~ △DEC
∴ \(\frac{\mathrm{BC}}{\mathrm{EC}}\) = \(\frac{\mathrm{AB}}{\mathrm{DE}}\)
⇒ \(\frac { 10 }{ 7 }\) = \(\frac { AB }{ 8 }\)
⇒ AB = \(\frac { 80 }{ 7 }\) = 11.43 miles.
OR
Given, DC = 5 + BC
Clearly, BC = 10 – 5 = 5 miles
Now, CE = \(\frac { 7 }{ 10 }\) × BC = \(\frac { 7 }{ 10 }\) × 5
= 3.5 miles