CBSE Sample Papers for Class 10 Maths Basic Set 6 with Solutions

Practicing the CBSE Sample Papers for Class 10 Maths Basic Set 6 allows you to get rid of exam fear and be confident to appear for the exam.

CBSE Sample Papers for Class 10 Maths Basic Set 6 with Solutions

Time Allowed : 3 hours
Maximum Marks : 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D, and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answer-II (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each) with sub-parts of the values of 1,1 and 2 marks each respectively.
7. All Questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take n = \(\frac{22}{7}\) wherever required if not stated.

Section – A
(Section A consists of 20 Questions of 1 marks each.)

Question 1.
The times, in seconds, taken by 150 athletes to run a 110 m hurdle race is tabulated below :

Class	13.8-14	14-14.2	14.2-14.4	14.4-14.6	14.6-14.8	14.8-15
Frequency	2	4	5	71	48	20

The number of athletes who completed the race in less than 14.6 seconds is :
(A) 11
(B) 71
(C) 82
(D) 130
Answer:
(C) 82

Explanation :
The number of athletes who completed the race in less than 14.6 seconds
=2 + 4 + 5 + 71
= 82

Question 2.
20 tickets, on which numbers 1 to 20 are written, are mixed thoroughly and then a ticket is drawn at random out of them the probability that the number on the drawn ticket is a multiple of 3 or 7 is:
(A) \(\frac{1}{5}\)
(B) \(\frac{2}{5}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{4}{5}\)
Answer:
(B) \(\frac{2}{5}\)

Explanation:
Total number of cases = 20
⇒ n(s) = 20
A = favourable cases = {3, 6, 7, 9, 12, 14, 15, 18}
∴ n(A) = 8 ½
∴ Required probability, P(A) = \(\frac{n(A)}{n(S)}\)
= \(\frac{8}{20}\) = \(\frac{2}{5}\)

Question 3.
The total surface area of a hemi-spherical solid having radius 14 cm is:
(A) 1488 cm²
(B) 1848 cm²
(C) 1844 cm²
(D) 1484 cm²
Answer:
(B) 1848 cm²

Explanation : The total surface area of hemisphere
= 3πr²
= 3 × \(\frac{22}{7}\) × (14)²
= \(\frac{3×22×14×14}{7}\)
= 1848 cm².

Question 4.
If the point C (k, 4) divides the join of points A(2,6) and B (5,1) in the ratio 2 : 3, then the value of k is : [1]
(A) 16
(B) \(\frac{18}{5}\)
(C) \(\frac{16}{5}\)
(D) \(\frac{8}{5}\)
Answer:
(C) \(\frac{16}{5}\)

Explanation :
By section formula,
m : n = 2 : 3
\(\frac{mx_2+nx_1}{m+n}\) = k,
\(\frac{my_2+ny_1}{m+n}\) = 4
Now, \(\frac{2×5×3×2}{2+3}\) = k
k = \(\frac{16}{5}\)

Question 5.
Given that cos θ = \(\frac{3}{2}\) then tan² θ is equal to
(A) \(\frac{1}{3}\)
(B) \(\frac{1}{\sqrt{3}}\)
(C) \(\frac{-1}{3}\)
(D) \(\frac{-1}{\sqrt{3}}\)
Answer:
(C) \(\frac{-1}{3}\)

Explanation:
Given, cos θ = \(\frac{3}{2}\)
1 + tan² θ = sec2 θ
and sec θ = \(\frac{1}{cos θ}\) = \(\frac{1}{3/2}\) = \(\frac{2}{3}\)
∴ 1 + tan² θ = \(\frac{2}{3}\) ⇒ tan² θ = \(\frac{2}{3}\) – 1 = \(\frac{-1}{3}\)

Question 6.
The value of 9 sec² A – 9 tan² A is:
(A) 1
(B) 9
(D) 8
(D) 0
Answer:
(B) 9

Explanation:
9 sec² A – 9 tan² A = −9(sec² A – tan² A)
= 9 (1)
[∵ sec² A – tan² A = 1]
= 9

Question 7.
The perpendicular distance of A(5,12) from the y-axis is:
(A) 5 units
(B) 6 units
(C) 3 units
(D) 7 units
Answer:
(A) 5 units

Explanation :
The point on the y-axis is (0, 12)
∴ Distance between (5, 12) and (0, 12) is
d = \(\sqrt{(0-5)^2 + (12-12)^2}\)
= \(\sqrt{25+0}\)
= 5 units

Question 8.
In an A.P, if d = – 4, n = 7, an = 4, then a is;
(A) 6
(B) 7
(C) 20
(D) 28
Answer:
(D) 28

Explanation :
In the given A.P.,
d = -4,
n = 7,
a_n = 4
a_n = a + (n – 1)d
⇒ 4 = a + (7 – 1)(-4) ⇒ a = 8

Question 9.
The first term of A.P is p and the common difference is q, then its 10th term is
(A) q + 9p
(B) p – 9q
(C) p + 9q
(D) 2p + 9q
Answer:
(C) p + 9q

Explanation:
a = p and d = q (given)
∴ 10th term = a + (10 – 1)d
= p + 9q

Question 10.
In figure, OR is common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :

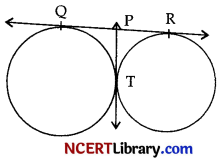
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
Answer:
(B) 7.6

Explanation :
Since,
QP = PT = 3.8 cm
(∴ tangents of circle)
and PR = PT = 3.8 cm
(∴ tangents of circle)
∴ QP = PR = 3.8 cm
QR = QP + PR
= 3.8 + 3.8
= 7.6

Question 11.
The distance between the pionts (0, 5) and (-5, 0) is:
(A) 5
(B) 5\(\sqrt{2}\)
(C) 2\(\sqrt{5}\)
(D) 10
Answer:
(B) 5\(\sqrt{2}\)

Explanation:
Distance between two points (x1, y1) and (x2, y2) is given as,
d = \(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Where, x₁ = 0,
y₁ = 5
and x₂ = -5, y₂ = 0
So, distance between the point (0, 5) and (-5, 0)
= \(\sqrt{(-5-0)^2+(0-5)^2}\)
= \(\sqrt{25+25}\)
= \(\sqrt{50}\)
= \(5 \sqrt{2}\)

Question 12.
325 can be expressed as a product of its primes as:
(A) 5² × 7
(B) 5² × 13
(C) 5 × 13²
(D) 2 × 3² × 5²
Answer:
(B) 5² × 13

Explanation:
By prime factorization,
325 = 5 × 5 × 13
= 5² × 13

Question 13.
If difference of two complimentary angles is 10°, then the two angles are:
(A) 10° and 80°
(B) 50° and 40°
(C) 20° and 80°
(D) 60° and 30°
Answer:
(B) 50° and 40°

Explanation:
We know that, sum of complimentary angles = 90°
Given, difference =10°
On solving x + y = 90°
and x – y = 10°
We get, x = 50° and y = 40°.

Question 14.
According to Fundamental Theorem of Arithmetic, Composite number = of prime numbers:
(A) Sum
(B) Product
(C) Difference
(D) Ratio
Answer:
(B) Product

Explanation:
According to fundamental theorem of arithmetic, we know that,
Composite number = Product of primes.

Question 15.
In the given figure, the angles of depressions from the observing positions 0| and 02 respectively of the object A.
(A) 30°, 45°
(B) 30°, 60°
(C) 30°, 30°
(D) 45°, 45°
Answer:
(A) 30°, 45°

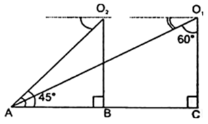
Explanation:

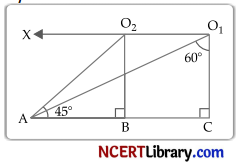
Draw O
O₁X || AC
∠AO₁X = 90° – 60° = 30°
and ∠AO₂X = ∠BAO₂ = 45°

Question 16.
Given that sin α = \(\frac{1}{2}\) and cos ß = \(\frac{1}{2}\) then the value of (α + ß) is
(A) 0°
(B) 30°
(C) 60°
(D) 90°
Answer:
(D) 90°

Explanation:
Given, sin α = \(\frac{1}{2}\) = sin 30°
[∵ sin 30° = \(\frac{1}{2}\)]
⇒ α = 30°
And, cos ß = \(\frac{1}{2}\) = cos 60°
⇒ ß = 60°
∴ α + ß = 30° + 60° = 90°

Question 17.
For an event E, P(E) + \(P \bar{(E)}\) = x, then the value of x³ – 3 is
(A) -2
(B) 2
(C) 1
(D) -1
Answer:
(A) -2

Explanation:
Given
P(E) + \(P \bar{(E)}\) = x …(i)
Also, according to the law of probability,
P(E) + \(P \bar{(E)}\) = 1 …(ii)
From (i) and (ii), we get
x = 1
Put value of x in x³ – 3, we get
x³ – 3 = (1)³ – 3 = 1 – 3 = -2

Question 18.
The probability that the drawn card from a pack of 52 cards is neither an ace nor a spade is
(A) \(\frac{9}{13}\)
(B) \(\frac{35}{52}\)
(C) \(\frac{10}{13}\)
(D) \(\frac{19}{26}\)
Answer:
(A) \(\frac{9}{13}\)

Explanation:
Total ace cards = 4 and total spade cards
= 13 – 1 = 12 (One card among aces is also a spade)
Cards which are neither ace or spade = 52 – 16 = 36
Required probability = \(\frac{36}{52}\) = \(\frac{9}{13}\)

Directions for Questions 19 and 20: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true but (R) is NOT the correct explanation of (A).
(C) (A) is true but (R) is false.
(D) (A) is false and (R) is true.

Question 19.
Assertion (A): The tangent to the circumcircle of an isosceles ∆ABC at A, in which AB = AC, is parallel to BC.
Reason (R): PQ is a tangent drawn from an external point P to a circle with centre O. QOR is the diameter of the circle. If ∠POR = 120°, then the measure of ∠OPQ is 60°.
Answer:
(C) (A) is true but (R) is false.

Explanation:
In case of assertion: given that, ΔABC, inscribed in a circle in which
AB = AC.

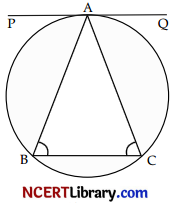
PAQ is tangent at A.
AB is chord.
∴ ∠PAB = ∠C …(i)
As, we know that, ∠PAB formed by chord AB with tangent is equal to ∠C formed by chord AC in alternate segment.
In ΔABC,
AB = AC [Given]
∴ ∠B = ∠C [∵ Angles opposite to equal sides are equal] …(ii)
From (i) and (ii),
∠B = ∠PAB
These are alternate interior angles.
∴ Assertion is correct.
In case of reason:

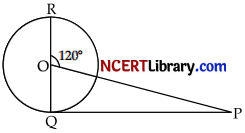
Given that,
PQ is a tangent, ∠POR = 120°
∠POR = ∠OQP + ∠OPQ
[Exterior angle sum property]
∠OPQ = 120° – 90° = 30°
∠OPQ = 30°
∴ Reason is incorrect.
Hence, assertion is correct but reason is incorrect.

Question 20.
Assertion (A): PQ is a tangent to a drde with centre O at point P. If ∆OPQ is an isosceles triangle, then ∠OQP = 45°.
Reason (R): If two tangents inclined at 60° are drawn to a circle of radius 3 cm, then the length of each tangent is 3^3 cm. 1
Answer:
(B) Both (A) and (R) are true but (R) is NOT the correct explanation of (A).

Explanation:
In case of assertion:
As we know that
∠OPQ = 90° (Angle between tangent and radius)
Let ∠PQO be x°, then
∠QOP = x°
Since OPQ is an isosceles triangle. (given)
(OP = OQ)

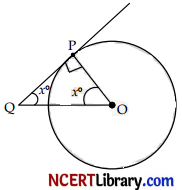
In ∆OPQ,
∠OPQ + ∠PQO + ∠QOP = 180°
(Property of the sum of angles of a triangle)
∴ 90° + x° + x° = 180°
⇒ 2x° = 180° – 90° = 90°
⇒ x = \(\frac{90}{2}\) = 45°
Hence, ∠OQP is 45°.
∴ Assertion is correct.
In case of reason:
∴ Reason is correct.
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.

Section – B
Section B consists of 5 Questions of 2 marks each.

Question 21.
Find k so that the quadratic equation (k + 1)x² – 2(k + 1)x + 1 =0 has equal roots.
OR
If one root of the quadratic equation 6x² – x – k = 0 is \(\frac{2}{3}\), then find the value of k.
Answer:
Since, (k + 1)x² – 2(k + 1)x + 1 = 0 has equal roots.
D = 0
⇒ b² = 4ac
⇒ 4(k + 1)² = 4(k + 1)
⇒ k² + 2k + 1 = k + 1
⇒ k² + k = 0
⇒ k(k + 1) = 0
⇒ k = 0 or – 1
k = – 1 does not satisfy the equation
So, k = 0
OR
On substituting x = \(\frac{2}{3}\), we get
6(\(\frac{2}{3}\))² – \(\frac{2}{3}\) – k = 0
6 × \(\frac{4}{9}\) – \(\frac{2}{3}\) – k = 0
k = 6 × \(\frac{4}{9}\) – \(\frac{2}{3}\)
∴ k = 2 1

Question 22.
In given figure, AB is the diameter of a circle with center O and AT is a tangent. If ∠AOQ = 58°, ∠ATQ. [2]

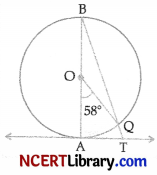
Answer:
∠AOQ = 58° (Given)
∠ABQ = \(\frac{1}{2}\)∠AOQ
[Angle on the circumference of the circle by the same arc]
= \(\frac{1}{2}\) × 58°
= 29°
∠BAT = 90° [∵ OA ⊥ AT]
∴ ∠ATQ = 90° – 29°
= 61°

Question 23.
In ∆ABC, if X and Y are points on AB and AC respectively such that \(\frac{AX}{XB}\) = \(\frac{3}{4}\), AY = 5 and YC = 9, then state whether XY and BC parallel or not. [2]
Answer:

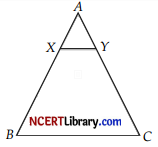
\(\frac{AX}{XB}\) = \(\frac{3}{4}\)
AY = 5
and YC = 9 (Given)
Then, \(\frac{AX}{XB}\) = \(\frac{3}{4}\)
and \(\frac{AY}{YC}\) = \(\frac{5}{9}\)
\(\frac{AX}{XB}\) ≠ \(\frac{AY}{YC}\)
Hence XY is not parallel to BC.

Question 24.
If sin A = \(\frac{1}{2}\),then find the value of 2 cot² A – 1.
OR
Prove that sin θ (1 + tan θ) + cos θ (1 + cot θ) = sec θ cosec θ. [2]
Answer:

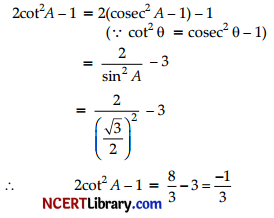
OR

Question 25.
Harpreet tosses two different coins simultaneously. What is the probability that she gets:
(i) atleast one head?
(ii) one head and one tail? [2]
Answer:
Possible outcomes are HH, TT, TH and HT.
(i) P(E₁) = \(\frac{3}{4}\)

(ii) P(E₂) = \(\frac{2}{4}\) = \(\frac{1}{2}\)

Section – C
Section C consists of 6 Questions of 3 marks each.

Question 26.
Find the values of p for which the quadratic equation 4x² + px + 3 = 0 has equal roots. [3]
OR
The p^th, q^th and r^th terms of an A.P are a, b and c respectively. Show that a(q – r) + b(r – p) + c(p -q) = 0.
Answer:
4x² + px + 3 = 0
Comparing equation with
ax² + bx + c = 0
a = 4,
b = p,
c = 3
For equal roots
D = b² – 4ac = 0
= p² – 4 × 4 × 3 = 0
p² – 48 = 0
p² = 48
p = ± \(\sqrt{48}\)
p = ± \(\sqrt{4 × 4 × 3}\)
p = ± 4\(\sqrt{3}\)
OR
Let the first term be a’ and the common difference be d.
a = a’ + (p – 1)d, b = a’ + (q – 1)d and c = a’ + (r – 1)d
a(q – r) = [a’ + (p – 1)d][q – r]
b(r – p) = [a’ + (q – 1)d][r – p]
and c(p – q) = [a’ + (r – 1)d][p – q]
∴ a(q – r) + b(r – p) + c(p – q)
= a’ [q – r + r – p + p – q] + d [(p – 1) (q – r) + (q – 1) (r – p) + (r – 1) (p – q)]
= a’ × 0 + d[pq – pr + qr – pq + pr – qr + (- q + r – r + p – p + q)] = 0
Hence Proved.

Question 27.
If P and q are the zeroes of polynomial f(x) = 2x² – 7x + 3, find the value of p² + q². [3]
OR
If x = \(\frac{2}{3}\) and x = – 3 are roots of the quadratic equation ax² + 7x + b = 0, find the values of a and b.
Answer:
Given f (x) = 2x² – 7x + 3
Sum of roots = p + q = –\(\frac{\text { Coefficient of x }}{\text { Coefficient of x² }}\)
= – \(\frac{-7}{2}\) = \(\frac{7}{2}\)
and Product of roots = pq = \(\frac{\text { Constant term }{\text { Coefficient of x² }}\)
= \(\frac{3}{2}\)
Since, (p + q)² = p² + q² + 2pq
so, p² + q² = (p + q)² – 2pq
= (\(\frac{7}{2}\))² – 3 = \(\frac{49}{4}\) – \(\frac{3}{1}\) = \(\frac{37}{4}\)
Hence, the value of p² + q² is \(\frac{37}{4}\)
OR
Substituting x = \(\frac{2}{3}\) in ax² + 7x + b = 0
\(\frac{4}{9}\)a + \(\frac{14}{3}\) + b = 0
⇒ 4a + 42 + 9b = 0
⇒ 4a + 9b = – 42 …(i) 1
Again, substituting x = – 3 in ax² + 7x + b = 0
i.e., 9a – 21 + b = 0
⇒ 9a + b = 21 …(ii) 1
Solving (i) and (ii), we get
a = 3
and b = – 6

Question 28.
If the distance of P(x, y) from A(6,2) and B(- 2,6) are equal, prove that y = 2x. [3]
Answer:
Given, P(x, y), A(6, 2) and B(- 2, 6).
PA = PB or, PA2 = PB
(x – 6)² + (y – 2)² = (x + 2)² + (y – 6)²
or, x² – 12x + 36 + y² – 4y + 4
= x² + 4x + 4 + y² – 12y + 36
or, – 12x – 4y = 4x – 12y
or, 12y – 4y = 4x + 12x
or, 8y = 16x
or, y = 2x
Hence Proved.

Question 29.
Given, ∆ABC ~ ∆DEF, find AC × DE and DE. [3]
Answer:
In ∆DEF,
DE = \(\sqrt{13^2 – 12^2}\)
= \(\sqrt{169 – 144}\) = \(\sqrt{25}\) = 5
\(\frac{A B}{D E}=\frac{A C}{D F}\) [From BPT]
⇒ \(\frac{3}{D E}=\frac{A C}{12}\)
Hence, AC × DE = 36 cm²

Question 30.
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [Use S = 1.73] [3]
Answer:
Height of flagstaff = CD = h m
Height of tower = BD = x m
∠ DAB = 45°,
∠ CAB = 60°
AB = 120 m

∆ ABD is right angled
tan 45° = 1
\(\frac{x}{AB}\) = 1
x = AB = 120 m ½
∆ACB is right angled
\(\frac{h+x}{120}\) = tan 60° = \(\sqrt{3}\)
h + 120 = 120 \(\sqrt{3}\)
h = 120 \(\sqrt{3}\) – 120
h = 120 (\(\sqrt{3}\) – 1)
h = 120 (1.73 – 1)
h = 120 × 0.73
h = 87.6 m
Hence, the height of the flagstaff = 87.6 m.

Question 31.
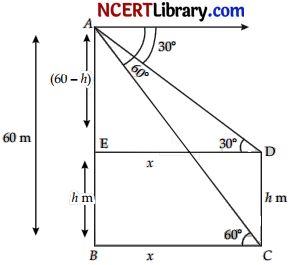
From the top of a building 60 m high the angles of depression of the top and the bottom of a tower are observed to be 30° and 60°. Find the height of the tower. [3]
Answer:
Let AB is a building 60 m high and x is a tower h m high. Angle of depressions of top and bottom are given 30° and 60° respectively.
DC = EB = h m and let BC = x m.
⇒ AE = (60 – h) m
In ∆AED, \(\frac{60 – h}{E D}\) = tan 30°
⇒ \(\frac{1}{\sqrt{3}}=\frac{60 – h}{E D}\)
⇒ \(\sqrt{3}\) (60-h) = x …(i)
In ∆ABC, \(\frac{60}{x}\) = tan 60°
⇒ 60 = \(\sqrt{3}\)x …(ii)
Putting the value of x from equation (i) in equation (ii), we get

60 = \(\sqrt{3}\) × \(\sqrt{3}\) (60 – h)
⇒ 60 = \(\sqrt{3}\) × (60 – h)
⇒ 20 = 60 – h
⇒ h = 40 m
Hence, the height of tower = 40 m.

Section – D
Section D consists of 4 Questions of 5 marks each.

Question 32.
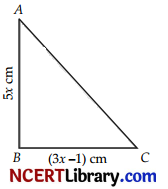
The length of the sides forming right angle of a right triangle are 5x cm and (3x – 1) cm. If the area of the triangle is 60 cm2. Find its hypotenuse. [5]
OR
Solve the following pair of equations graphically:
2x + 3y = 12 and x-y -1 =0.
Shade the region between the two lines represented by the above equations and the X-axis.
Answer:

Area of triangle = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 5x × (3x – 1)
According to the question,
Area of triangle = 60
⇒ \(\frac{1}{2}\) × 5x × (3x – 1) = 60
⇒ 15x² – 5x = 120
⇒ 3x² – x – 24 = 0
⇒ 3x² – 9x + 8x – 24 = 0 1
⇒ 3x (x – 3) + 8 (x – 3) = 0
⇒ (x – 3) (3x + 8) = 0
∴ x = 3 or x = – \(\frac{8}{3}\)
But length can’t be negative, so x = 3
AB = 5 × 3 = 15 cm and BC = 3x – 1 = 9 – 1
= 8 cm
∴ AC = \(\sqrt{15^2 + 8^2}\)
= \(\sqrt{225 + 64}\)
= \(\sqrt{289}\)
= 17 cm
Hence, hypotenuse = 17 cm
OR
Given, 2x + 3y = 12
⇒ y = \(\frac{12-2x}{3}\)

x	0	6	3
y	4	0	2

and x – y = 1
⇒ y = x – 1

x	0	1	3
y	-1	0	2

Plotting the above points and drawing the lines joining them, we get the above graph.
The two lines intersect each other at point C(3, 2),
Hence, x = 3 and y = 2. 1
Thus, ∆ABC is the region between the two lines
represented by the given equations and the X-axis.

Question 33.
Two circular beads of different sizes are joined together such that the distance between their centres is 14 cm. The sum of their areas is 130π cm². Find the radius each bead. [5]
OR
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB. [5]

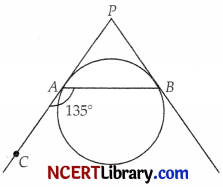
Answer:
Let the radii of the circles are r₁ cm and r₂ cm.
∴ r₁ + r₂ = 14 …(i)
and sum of their areas = πr₁² + πr₂²
130 π = π(r₁² + r₂²)
or, 130 π = π(r₁² + r₂²)
∴ r₁² + r₂² = 130 …(ii)
(r₁ + r₂)² = r₁² + r₂² + 2r₁r₂
or, (14)² = 130 + 2r₁r₂
or, 2r₁r₂ = 196 – 130 = 66
(r₁ – r₂)² = r₁² + r₂² – 2r₁r₂
= 130 – 66 = 64
or, r₁ – r₂ = 8 …(iii)
From (i) and (iii), 2r₁ = 22
or, r₁ = 11 cm
and r₂ = 14 – 11
= 3 cm
OR
PA = PB = 4 cm
(Tangents from external point)
∠PAB = 180° – 135° = 45°
(Supplementary angles)
∠ABP = ∠PAB = 45°
(Opposite angles of equal sides)
∴ ∠APB = 180° – 45° – 45°
= 90°
So, ∆ABP is an isosceles right angled triangle.
⇒ AB² = 2AP²
⇒ AB² = 32
Hence, AB = \(\sqrt{32}\) = 4\(\sqrt{2}\) cm

Question 34.
From a solid right circular cylinder of height 14 cm and base radius 6 cm, a right circular cone of same height and same base removed. Find the volume of the remaining solid. [5]
Answer:
Given, Height (h) = 14 cm
and Base radius (r) = 6 cm
Volume of the remaining solid = Volume of a right circular cylinder – Volume of a rightcircular cone
= πr²h – \(\frac{1}{3}\)πr²h
= \(\frac{2}{3}\)πr²h
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 6 × 6 × 14
=1056 cm³

Question 35.
Following frequency distribution shows the daily expenditure on milk of 30 households in a locality:

Daily expenditure on milk (in ₹)	0-30	30-60	60-90	90 -120	120 -150
Number of households	5	6	9	6	4

Find the mode for the above data.
Answer:
Here, maximum frequency = 9, hence modal class is 60 – 90.

Section – E
Case study based questions are compulsory.

Question 36.
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.

I. What are the values taken by the terms a, b and c in the standard form of quadratic polynomial, ax²+ bx + c?
II. If the roots of the quadratic polynomial are equal, then find the value of discriminant. 2
III. If a are \(\frac{1}{α}\) the zeroes of the quadratic polynomial 2x² – x + 8k, then find value of k.
OR
At what points the graph of x² + 1 = 0 touches or intersects the x-axis?
Answer:
I. ‘a’ is a non zero real number and b and c are any real numbers.
II. If the roots of the quadratic polynomial are equal, then discriminant is equal to zero
i.e., D = b² – 4ac = 0. 1
III. Given equation, 2x² – x + 8k
Sum of zeroes = α + \(\frac{1}{α}\)
Product of zeroes = α\(\frac{1}{α}\) = 1
Product of zeroes = \(\frac{c}{a}\) = \(\frac{8k}{2}\)
So, \(\frac{8k}{2}\) = 1
k = \(\frac{2}{8}\)
k = \(\frac{1}{4}\)
OR
Given, x² + 1 = 0
⇒ x² = – 1
⇒ x = \(\sqrt{-1}\)
Here, x does not take real values.
Hence, the graph of x² + 1 = 0, neither touches nor intersects the x-axis.

Question 37.
On a Sunday, your parents took you to a fair. You could see lot of toys displayed, and you wanted them to buy a RUBIK’s cube and strawberry ice-cream for you. [5]

Find the length of the diagonal if each edge measures is 6 cm.
II. What is the curved surface area of hemisphere (ice cream) if the base radius is 7 cm ?
III. Find the slant height of a cone if the radius is 7 cm and the height is 24 cm.
OR
The total surface area of cone with hemispherical ice cream is:
Answer:
I. We know that
Length of the diagonal = \(\sqrt{3}\) × side
Length of the diagonal of cube with edge 6 cm
= \(\sqrt{3}\) × 6 = 6\(\sqrt{3}\) cm

II. We know that,
CSA(curved surface area) of hemisphere = 2πr²
Given, r = 7 cm
So, CSA = 2 × \(\frac{22}{7}\) × 7 × 7
= 308 cm²

III. Slant height of cone,
l = \(\sqrt{r^2 + h^2}\)
Hence, r = 7 cm
and h = 24 cm
∴ l = \(\sqrt{7^2 + 24^2}\)
= \(\sqrt{625}\) = 25 cm
OR
Total surface area of the cone with hemispherical ice-cream
= curved surface area of the cone + curved surface area of the hemisphere
= 550 + 308
[∵ curved surface area of cone = πrl = \(\frac{22}{7}\) × 7 × 25 = 550 cm²]
= 858 cm²

Question 38.
To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- section A and section B of grade X. There are 32 students in section A and 36 students in section B.

I. What is the minimum number of books you will acquire for the class library, so that they can be distributed equally among students of Section A or Section B?
II. If the product of two positive integers is equal to the product of their HCF and LCM is true then, find the HCF (32,36).
III. Prove that the product of the numbers is equal to the product of HCF and LCM from question part (i) and (ii).
Is it true that 7 × 11 × 13 × 15 + 15 is a composite number?
Answer:
I. We have to find the LCM of 32 and 36.
LCM (32, 36) = 2⁵ × 9 = 288
Hence, the minimum number of books required to distribute equally among students of section A and section B are 288.

II. Prime factors of 32 = 2⁵
and prime factors of 36 = 2² × 3²
∴ HCF = 2² = 4

III. Product of two number = 32 × 36
= 1152
Product of HCF × LCM = 288 × 4
= 1152
Hence Proved.
OR
7 × 11 × 13 × 15 + 15 = 15 (7 × 11 × 13 + 1)
= 15 × 1002
Hence, it is ture that given number is a composite number.