Refraction of Light
When light travels from one medium to another, there is a change in its direction due to a change in speed of light. Consider a pencil that is partly immersed in water. The light reaching us from the portion of the pencil inside water seems to come from a different direction, compared to the part above water due to which the pencil appears to be displaced at the interface.
Example 1.
Case Based:
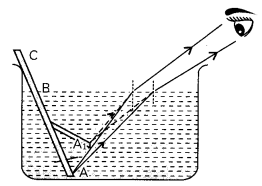
First, place a coin at the bottom of a bucket filled with water. With your eye to a side above water, try to pick up the coin in one go. Repeat the Activity.
Next, place a large shallow bowl on a table and put a coin in it. Move away slowly from the bowl. Stop when the coin just disappears from your sight. Ask a friend to pour water gently into the bowl without disturbing the coin. Keep looking for the coin from your position.
(A) Refer to the first activity. When a coin is placed at the bottom of a bucket filled with water and we try to pick up the coin with our eye to a side above the water:
(a) We are able to pick up the coin in one go
(b) We are able to pick up the coin but the coin slips from our hands as it is wet
(c) We are unable to pick up the coin as the water is too deep
(d) We are unable to pick up the coin in one go as the coin appears to be raised when kept in water.
Answer:
(d) We are unable to pick up the coin in one go as the coin appears to be raised when kept in water.
Explanation: The coin placed in water in a bucket appears to be raised as light rays travel from an optically denser medium (water) to an optically rarer medium (air) and hence bend away from the normal when they reach our eyes. The coin therefore appears to be raised.

(B) In the second activity, the coin placed in a shallow bowl disappears when we move away from the bowl. When water is poured gently into the bowl:
(a) The coin will still not be visible
(b) The coin becomes visible again
(c) The coin appears to be at the bottom of the bowl
(d) The coin appears to be on the water surface.
Answer:
(b) The coin becomes visible again
Explanation: When water is gently poured into the bowl, the coin becomes visible again because due to refraction of Light travelling from water to air, the submerged coin seems raised to be above its actual level and thus becomes visible on seeing from the same side and distance. The coin appears slightly raised above its actual position due to refraction of light.
(C) What will be the absolute refractive index of a medium in which speed of light is 1.8 × 108 m/s?
Answer:
The absolute refractive index of a medium in which speed of light is 1.8 × 108 m/s will be 1.67.
Explanation: The absolute refractive index of a medium is defined as the ratio of speed of light in air or vacuum to the speed of light in the medium.
na = \(\frac{c}{v_{a}}=\frac{3 \times 10^{8}}{1.8 \times 10^{8}}=\frac{3}{1.8}\) = 1.67
(D) In which direction will light bend when it travels from a medium having refractive index 2.3 to a medium having refractive index 1.8?
Answer:
Light will bend away from the normal when it travels from the medium having refractive index 2.3 towards the medium having refractive index 1.8.
Explanation: A medium having refractive index 2.3 is optically more denser as compared to a medium having a refractive index 1.8. Therefore, light will bend away from the normal when it travels from the medium having refractive index 2.3 towards the medium having refractive index 1.8.
(E) Assertion (A): A coin kept in a shallow bowl appears to be raised.
Reason (R): Light rays undergo refraction and bend away from the normal when they travel from water to air.
(a) Both (A) and (R) are true and (R) is the correct explanation of the (A).
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the (A).
(c) (A) is true, but (R) is false.
(d) (A) is false, but(R) is true.
Answer:
(d) (A) is false, but (R) is true.
Explanation: When a coin is kept in a shallow bowl, there is no change in its apparent position as no refraction of light takes place. However, when it is kept in water, light undergoes refraction as it travels from water, which is an optically denser medium, to air, an optically rarer medium. Light rays bend away from the normal and hence the coin appears to be raised when kept in water.
Laws of Refraction
The following are the laws of refraction:
- The incident ray, the refracted ray and the normal to the surface of separation of two media at the point of incidence, all lie in the same plane.
- Snell’s law: The ratio of sine of the angle of incidence / to the sine of angle of r is constant. We can write sin i/sin r = n21, where n21 is a constant and is called the refractive index of medium 2 with respect to medium 1.
The Refractive index
The refractive index of medium 2 with respect to medium 1 is defined as the ratio of the speed of light in first medium (v1) to the speed of light in the second medium (v2). It is linked to the relative speed of propagation of light in different media.
n21 = \(\frac{\text { Speed of light in first medium }\left(\mathrm{v}_{1}\right)}{\text { Speed of light in second medium }\left(\mathrm{v}_{2}\right)}\)
Absolute refractive index
The refractive index of a medium with respect to vac-uum is called the absolute refractive index (the first medium is free space or vacuum). The refractive index of water is 1.33, which means that the ratio of speed of light in air and the speed of light in water is 1.33.
n = \(\frac{\text { Speed of light in vacuum (c) }}{\text { Speed of light in the medium (v’) }}\)
An optically denser medium may not possess greater mass density.
Snell’s law in terms of absolute refractive index
If n1 and n2 are the refractive indices of the first and the second medium with respect to vacuum, and the speed of light in the first and second medium is v1 and v2 respectively, Snell’s law can be written as,
n21 = \(\frac{\sin i}{\sin r}=\frac{v_{1}}{v_{2}}=\frac{\left(c / n_{1}\right)}{\left(c / n_{2}\right)}=\frac{n_{2}}{n_{1}}\)
Optically denser medium
A medium that has a larger refractive index as compared to another medium is called an optically denser medium. A ray of light travelling from a rarer medium to a denser medium bends towards the normal.
Optically rarer medium
A medium that has a lower refractive index as compared to another medium is called an optically rarer medium. The speed of light is higher in a rarer medium than in a denser medium. Thus a ray of light travelling from a rare medium to a denser medium slows down and bends towards the normal.
Example 2.
The refractive index of diamond is 2.42. What is the meaning of this statement?
Answer:
The refractive index of diamond = 2.42 means
that 2.42 = \(\frac{c}{v}=\frac{3 \times 10^{8}}{v} \Rightarrow v=\frac{3 \times 10^{8}}{2.42}\)
where v = speed of light in diamond.
So, the statement means that the speed of light in diamond is less than the speed of light in vacuum by a factor of 2.42.
Refraction Through a Glass Slab
When a ray of light is incident from air (rarer medium) on a glass slab (denser medium), it bends towards the normal and when it emerges from the glass slab, the. emergent ray is parallel to the incident ray but is laterally displaced. The lateral displacement is proportional to the thickness of the glass slab.

To find the refractive index of two media with respect to each other: Consider three transparent media 1, 2 and 3 having refractive indices n1 n2 and n3 respectively. Then, the refractive index of medium 3 with respect to medium 2 is given as,
n32 = \(\frac{n_{3}}{n_{2}}=\frac{n_{3} / n_{1}}{n_{2} / n_{1}}=\frac{n_{31}}{n_{21}}\) = n31 × n12
Refraction by Spherical Lenses
A lens is formed by joining together two refracting surfaces. A transparent material bound by two surfaces, of which one or both surfaces are sphericaL, forms a lens. This means that a lens is bound by at atleast one spherical surface. In such lenses, the other surface would be plane.

Convex tens: A Lens may have two spherical surfaces. bulging outwards. Such a Lens is called a double convex lens. It is simply called a convex lens. It is thicker at the middle as compared to the edges. Convex Lens converges light rays as shown in Fig. (a). Hence convex tenses are called converging lenses, Concave lens: A double concave tens is bounded by two spherical surfaces. curved inwards. It is thicker at the edges than at the middle. Such lenses diverge light rays as shown in Fig. (b). Such lenses are called diverging lenses. A double concave lens is simply called a concave lens.
A lens, either a convex lens or a concave lens, has two spherical surfaces. Each of these surfaces forms a part of a sphere.
Centre of curvature: The centres of spheres of which the lens is a part are called centres of curvature of the lens. The centre of curvature of a lens is usually represented by the letter C. Since there are two centres of curvature, we may represent them as C1 (2F1)and C2(2F2).
Principal axis: An imaginary straight line passing through the two centres of curvature of a lens is called its principal axis.
Optical centre: The central point of a lens is its optical centre. It is usually represented by the letter O. A ray of light through the optical centre of a lens passes without suffering any deviation.
Aperture: The effective diameter of the circular outline of a spherical lens is called its aperture. Lenses whose aperture is much less than its radius of curvature are called thin lenses with small apertures. If you pass parallel rays from the opposite surface of the lens, you get another principal focus on the opposite side. Letter F is usually used to represent the principal focus. However, a lens has two principal foci. They are represented by Fi and F2.
Focal length: The distance of the principal focus from the optical centre of a lens is called its focal length. The letter f is used to represent the focal length.
Image Formation in Lenses
To understand the formation of images by a lens, the following rules should be considered:
1. A ray from the object and parallel to the principal. axis posses through the second principal focus F2 (in convex tens) or appears to diverge (in concave tens) from the first principaL focus. F1.

2. A ray of Light passing through the principal focus emerges parallel to the principal axis after refraction from a convex lens. A ray of tight appearing to meet at the principal focus of a concave lens will emerge paraLleL to the principal axis after refraction.


3. A ray of Light passing through the optical centre does not suffer any deviation.

The image formed by a convex Lens: The table below lists the position and nature of the image formed by a convex lens for different positions of the object.

The image formed by a concave Lens:

When a concave lens made of a material of refractive index n1 is kept in a medium of refractive index n2 and a parallel beam of light is incident on the lens, the following figures show the path of rags of Light emerging from the concave Lens if (i) n1 > n2 (ii) n1 = n2 (iii) n1< n2.

Sign Conventions with Spherical Lenses
- Sign conventions are the same as in spherical mirrors but here, all measurements are taken from the optical centre of the lens.
- Focal length of a convex lens is positive and that of a concave lens is negative.
Lens formula:
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\), where
u = object distances
v = image distance
f = Focal length
Magnification produced by a lens: It is defined as the ratio of the size of the image to the size of the object. Thus, magnification, m = \(\frac{\text { Size of image }}{\text { Size of object }}=\frac{h^{\prime}}{h}=\frac{v}{u}\)
Magnification is always positive in case of a concave mirror as it always produces a virtual and erect image.
In case of convex lens, Magnification is positive when the image formed is virtual and negative when image formed is real.
Example 3.
Which of the following lenses would you prefer to use while reading small letters found in a dictionary?
(a) A convex lens of focal length 50 cm.
(b) A concave lens of focal length 50 cm.
(c) A convex lens of focal length 5 cm.
(d) A concave lens of focal length 5 cm.
Answer:
(c) A convex lens of focal length 5 cm.
Explanation: Convex lens is used for reading small letters found in a dictionary. This is because it magnifies or enlarges the image of the object. As convex lens of shorter focal length has greater power as compared to convex lens of greater focal length, we will use convex lens of focal length 5 cm.
Example 4.
A concave lens of focal length 15 cm forms an image 10 cm from the lens. How far is the object placed from the lens? Draw the ray diagram.
Answer:
Given, f = – 15 cm, v = – 10 cm (minus sign is taken as a concave lens always forms a virtual image).
To find the object distance, we will use the lens formula \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
Therefore, \(\frac{1}{u}=\frac{1}{v}-\frac{1}{f}=-\frac{1}{10}+\frac{1}{15}\)
\(=\frac{-3+2}{30}=-\frac{1}{30}\) ⇒ u = -30 cm
The object is placed 30 cm in front of the concave lens as shown in the ray diagram:

Power of a Lens
The power of lens is a measure of the degree of convergence or divergence of light rays falling on it and is defined as the reciprocal of its focal length.
P = \(\frac{1}{f}\)
Dioptre: The SI unit of power of a lens is dioptre (D) and is defined as the power of a lens whose focal length is 1 metre.
Important
The power of a concave lens is negative and that of a convex lens is positive. The power of a lens is more if it has a short focal length.
Example 5.
A doctor has prescribed a corrective lens of power +1.5 D. Find the focal length of the lens. Is the prescribed lens diverging or converging?
Answer:
The relation between power and focal Length of a lens is given by:
P(in D) = \(\frac{1}{f(\text { in } m)}\) ⇒ f(in m) = \(\frac{1}{P}=\frac{1}{1.5}\) = 0.66
As power (and hence focal length) is positive, the lens is convex having focal length 0.66 m or 66.66 cm.
Power of a combination of lenses: The net power of a combination of lenses is given by the algebraic sum of the individual powers P1 P2, P3,… of the lenses in contact, as
P = P1 + P2 + P3 + ………………..
The use of powers, instead of focal lengths, for lenses is quite convenient for opticians. The simple additive property of the powers of lenses can be used to design lens systems to minimise certain defects in images produced by a single lens. Such a lens system, consisting of several lenses, in contact, is commonly used in the design of camera lenses and the objectives of microscopes and telescopes.