NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.6
Get Free NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.6 PDF in Hindi and English Medium. Sets Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. Sets Exercise 1.6 Class 11 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 1 Class 11 Sets Ex 1.6 provided in NCERT Textbook.
- Class 11 Sets Ex 1.1
- Class 11 Sets Ex 1.1 in Hindi Medium
- Class 11 Sets Ex 1.2
- Class 11 Sets Ex 1.2 Hindi Medium
- Class 11 Sets Ex 1.3
- Class 11 Sets Ex 1.3 Hindi Medium
- Class 11 Sets Ex 1.4
- Class 11 Sets Ex 1.4 Hindi Medium
- Class 11 Sets Ex 1.5
- Class 11 Sets Ex 1.5 Hindi Medium
- Class 11 Sets Ex 1.6
- Class 11 Sets Ex 1.6 Hindi Medium
- Class 11 Sets Miscellaneous Exercise
- Class 11 Sets Miscellaneous Exercise in Hindi Medium
- Sets Class 11 Notes Maths Chapter 1
- NCERT Exemplar Class 11 Maths Chapter 1 Sets
- RD Sharma Class 11 Solutions Chapter 1 Sets
- Chapter 1: Sets Class 11 NCERT Book
- अध्याय 1: समुच्चय Class 11 NCERT Book
Free download NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.6 PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.
Class 11 Maths NCERT Solutions Chapter 1 Sets Ex 1.6
Q.1: If A and B are two sets such that n(A) = 16, n(B) = 24 and n(A∪B) = 39. Find n(A∩B).
Solution:
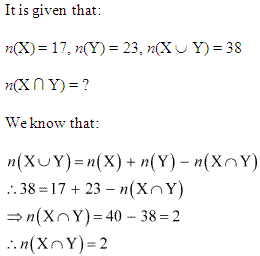
Q.2: If A and B are two sets such that A∪B has 17 elements, A has 9 elements and B has 14 elements. How many elements does A∩B have?
Solution:

Q.3: In a group there are 450 people, 200 speaks Hindi and 270 can speak English. How many people can speak both English and Hindi?
Solution:

Q.4: If X and Y are two sets such that X has 22 elements, Y has 34 elements, and n(X∩Y) has 10 elements, how many elements does n(X∪Y) have?
Solution:

Q.5: If A and B are two sets such that A has 45 elements, n (A ∩ B) has 15 elements and n (A ∪ B) has 70 elements, how many elements does B have?
Solution:

Q.6:There are 70 people, out of which 35 like tea, 55 like coffee, and each person likes at least one of the two beverages. How many people like both tea and coffee?
Solution:

Q.7: There are 70 students in a group, 35 like cricket, 15 like both tennis and cricket. How many like tennis only and not cricket? How many like tennis?
Solution:

Q.8: In a committee, 60 people speak French, 30 speak Spanish and 20 speak both Spanish and French. How many speak at least one of these two languages?
Solution:

NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.6 in Hindi

प्रश्न 4.
यदि S और T दो ऐसे समुच्चय हैं कि S में 21, T में 32 और S ∩ T में 11 अवयव हों तो S ∪T में कितने अवयव होंगे?
हल:
यहाँ n(S) = 21, n (T) = 32, n(S ∩T) = 11
n(S∪T) = n(S) + n(T) – n(S ∩ T) = 21 + 32 – 11 = 53 – 11 = 42.
प्रश्न 5.
यदि X और दो ऐसे समुच्चय हैं कि X में 40, X ∪Y में 60, और X ∩ Y में 10 अवयव हों, तो ? में कितने अवयव होंगे?
हल:
n(X) = 40, n(X ∪Y) = 60, n(X ∩ Y) = 10, n(Y) = ?
n(X ∪ Y) = n(X) + n(Y) – n (X ∩Y)
60 = 40 + n (Y) – 10
n(Y) = 60 – 40 + 10 = 30.
प्रश्न 6.
70 व्यक्तियों के समूह में 37 कॉफी, 52 चाय पसंद करते हैं और प्रत्येक व्यक्ति दोनों में से कम से कम एक पेय पसंद करता है, तो कितने व्यक्ति कॉफी और चाय दोनों पसंद करते हैं?
हल:
मान लिया C, कॉफी पीने वाले लोगों के समुच्चय को और T, चाय पीने वाले लोगों के समुच्चय हों, तब
n(C ∪T) = 70, n(C) = 37, n(T) = 52
n(C ∪T) = n (C) +n(T) – n(C ∩ T)
70 = 37 + 52 – n(C ∩T)
n(C ∩ T) = 37 + 52 -70 = 89 – 70 = 19.
प्रश्न 7.
65 व्यक्तियों के समूह में, 40 व्यक्ति क्रिकेट और 10 व्यक्ति क्रिकेट तथा टेनिस दोनों को पंसद करते हैं, तो कितने व्यक्ति केवल टेनिस को पंसद करते हैं किंतु क्रिकेट को नहीं? कितने व्यक्ति टेनिस को पंसद करते हैं?
हल:
मान लीजिए C, क्रिकेट पंसद करने वाले लोगों का समुच्चय है और T टेनिस पंसद करने वालों का समुच्चय हो, तब
n(C ∪T) = 65, n(C) = 40, n(C ∩T) = 10
हम जानते हैं कि
n(C ∪ T) = n(C) + n(T) – n(C ∩ T)
65 = 40 + n(T) – 10 = 30 + n(T)
n(T) = 65 – 30 = 35
केवल टेनिस पंसद करने वालो की संख्या = n(T) – n(C ∩T) = 35 – 10 = 25.
इस प्रकार टेनिस पंसद करने वालों की संख्या जो क्रिकेट पंसद नहीं करते = 25
अत: टेनिस पंसद करने वाले लोगों की संख्या = 35.
प्रश्न 8.
एक कमेटी में, 50 व्यक्ति फ्रेंच 20 व्यक्ति स्पेनिश और 10 व्यक्ति स्पेनिश और फ्रेंच दोनों ही भाषाओं को बोल सकते हैं। कितने व्यक्ति इन दोनों ही भाषाओं में से कम से कम एक भाषा बोल सकते हैं?
हल:
मान लीजिए फ्रांसीसी बोलने वाले लोगों के समुच्चय को F से तथा स्पैनिश बोलने वाले लोगों के समुच्चय का S से निरुपित किया हो, तब
n(F) = 50, n(S) = 20, n(F ∩S) = 10
अब, n(F ∪S) = n(F) + n (S) – n (F ∩S) = 50 + 20 – 10 = 60
कम से कम एक भाषा बोलने वाले लोगों की संख्या = 60.