NCERT Exemplar Class 6 Maths Chapter 7 Algebra are part of NCERT Exemplar Class 6 Maths. Here we have given NCERT Exemplar Class 6 Maths Solutions Chapter 7 Algebra.
NCERT Exemplar Class 6 Maths Chapter 7 Algebra
Directions: In questions 1 to 23, out of the four given options, only one is correct. Write the correct answer.
Question 1.
If each match box contains 50 matchsticks, the number of matchsticks required to fill n such boxes is
(A) 50 + n
(B) 50n
(C) 50 + n
(D) 50 – n
Solution:
(B)
Number of matchsticks in one box = 50
∴ The number of matchsticks required to fill n boxes = 50 × n = 50n
Question 2.
Amulya is x years of age now. 5 years ago her age was
(A) (5 – x) years
(B) (5 + x) years
(C) (x – 5) years
(D) (5 + x) years
Solution:
(C)
The present age of Amulya is x years.
∴ 5 years ago, her age was (x – 5) years.
Question 3.
Which of the following represents 6 × x
(A) 6x
(B) \(\frac{x}{6}\)
(C) 6 + x
(D) 6 – x
Solution:
(A)
6 × x can be represented as 6x.
Question 4.
Which of the following is an equation?
(A) x + 1
(B) x – 1
(C) x – 1 = 0
(D) x + 1 > 0
Solution:
(C)
Equation means an expression with a variable, constants and the sign of equality (=).
∴ x – 1 = 0 is an equation.
Question 5.
If x takes the value 2, then the value of x + 10 is
(A) 20
(B) 12
(C) 5
(D) 8
Solution:
(B)
When we put x = 2 in the given expression x + 10, we get
x + 10 = 2 + 10 = 12
Question 6.
If the perimeter of a regular hexagon is x metres, then the length of each of its sides is
(A) (x + 6) metres
(B) (x ÷ 6) metres
(C) (x – 6) metres
(D) (6 ÷ x) metres
Solution:
(B)
Perimeter of a regular hexagon = 6 × Length of each side
⇒ x m = 6 × Length of each side
⇒ Length of each side = (x ÷ 6) m
Question 7.
Which of the following equations has x = 2 as a solution?
(A) x+ 2 = 5
(B) x- 2 = 0
(C) 2x + 1 = 0
(D) x + 3 = 6
Solution:
(B)
(A) Putting x = 2 in x + 2, we get 2 + 2 = 4 ≠ 5
(B) Putting x = 2 in x – 2, we get 2 – 2 = 0
(C) Putting x = 2 in 2x + 1, we get 2 × 2 + 1 = 5 ≠ 0
(D) Putting x = 2 in x + 3, we get 2 + 3 = 5 + 6
Thus, the above conditions shows that x = 2 is the solution of x – 2 = 0
Question 8.
For any two integers x and y, which of the following suggests that operation of addition is commutative?
(A) x + y = y + x
(B) x + y > x
(C) x – y = y – x
(D) x × y = y × x
Solution:
(A)
x + y = y + x shows that addition is commutative.
Question 9.
Which of the following equations does not have a solution in integers?
(A) x + 1 = 1
(B) x – 1 = 3
(C) 2x + 1 = 6
(D) 1 – x = 5
Solution:
(C)
(A) x + 1 = 1
⇒ x + 1 – 1 = 1 – 1
[Subtracting 1 from both sides]
⇒ x = 0, which is an integer
(B) x – 1 = 3
⇒ x – 1 + 1 = 3 + 1 [Adding 1 to both sides]
⇒ x = 4, which is an integer.
(C) 2x + 1 = 6
⇒ 2x + 1 – 1 = 6 – 1
[Subtracting 1 from both sides]
⇒ 2x = 5
\(\frac{2 x}{2}=\frac{5}{2}\)
[Dividing both sides by 2]
⇒ \(x=\frac{5}{2}\), which is not a integer
(D) 1 – x = 5
⇒ 1 – x – 1 = 5 – 1
[Subtracting 1 from both sides]
⇒ -x = 4
⇒ -(-x) = -4
[Multiplying both sides by (-1)]
⇒ x = -4, which is an integer.
Thus, the above conditions show that equation 2x + 1 = 6 does not have a solution in integers.
Question 10.
In algebra, a × b means ab, but in arithmetic 3 × 5 is
(A) 35
(B) 53
(C) 15
(D) 8
Solution:
(C)
3 × 5 means 15.
Question 11.
In algebra, letters may stand for
(A) known quantities
(B) unknown quantities
(C) fixed numbers
(D) none of these
Solution:
(B)
In algebra, letters may stand for unknown quantities.
Question 12.
“Variable” means that it
(A) can take different values
(B) has a fixed value
(C) can take only 2 values
(D) can take only three values
Solution:
(A)
“Variable” means that it can take different values.
Question 13.
10 – x means
(A) 10 is subtracted x times
(B) x is subtracted 10 times
(C) x is subtracted from 10
(D) 10 is subtracted from x
Solution:
(C)
10 – x means x is subtracted from 10.
Question 14.
Savitri has a sum of Rs. x. She spent Rs. 1000 on grocery, Rs. 500 on clothes and Rs. 400 on education, and received Rs. 200 as a gift. How much money (in Rs.) is left with her?
(A) x – 1700
(B) x – 1900
(C) x + 200
(D) x – 2100
Solution:
(A)
Amount of money Savitri has = Rs. x.
Amount of money spent by her
= Rs. (1000 + 500 + 400) = Rs. 1900
Amount of money received by her as a gift = Rs. 200
∴ Amount of money left with her = Rs. (x – 1900 + 200)
= Rs. (x – 1700)
Question 15.
The perimeter of the triangle shown in the given figure is
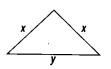
(A) 2x + y
(B) x + 2y
(C) x + y
(D) 2x – y
Solution:
(A)
The perimeter of the triangle = Sum of all sides = x + x + y = 2 x + y
Question 16.
The area of a square having each side x is
(A) x × x
(B) 4x
(C) x + x
(D) 4 + x
Solution:
(A)
The area of a square = (side) × (side) = x × x
Question 17.
The expression obtained when x is multiplied by 2 and then subtracted from 3 is
(A) 2x – 3
(B) 2x + 3
(C) 3 – 2x
(D) 3x – 2
Solution:
(C)
x is multiplied by 2 and then subtracted from 3 = 3 – 2 × x = 3 – 2x
Question 18.
\(\frac{q}{2}=3\) has a solution
(A) 6
(B) 8
(C) 3
(D) 2
Solution:
(A)
We have, \(\frac{q}{2}=3\)
Multiplying both sides by 2, we get
⇒ \(\frac{q}{2} \times 2=3 \times 2\)
⇒ q = 6
Question 19.
x – 4 = -2 has a solution
(A) 6
(B) 2
(C) -6
(D) -2
Solution:
(B)
We have, x – 4 = – 2 ⇒ x – 4 + 4 = -2 + 4
[Adding 4 to both sides]
⇒ x = 2
Question 20.
\(\frac{4}{2}=2\) denotes a
(A) numerical equation
(B) algebraic expression
(C) equation with a variable
(D) false statement
Solution:
(A)
\(\frac{4}{2}=2\) denotes a numerical equation.
Question 21.
Kanta has p pencils in her box. She puts q more pencils in the box. The total number of pencils with her are
(A) p + q
(B) pq
(C) P – q
(D) \(\frac{p}{q}\)
Solution:
(A)
Kanta has p pencils in her box.
After putting q more pencils in the box, she has total number of pencils = p + q.
Question 22.
The equation 4x = 16 is satisfied by the following value of x
(A) 4
(B) 2
(C) 12
(D) -12
Solution:
(A)
We have, 4x = 16
⇒ \(\frac{4 x}{4}=\frac{16}{4}\)
[Dividing both sides by 4]
⇒ x = 4
Question 23.
I think of a number and on adding 13 to it, I get 27. The equation for this is
(A) x – 27 = 13
(B) x – 13 = 27
(C) x + 27 = 13
(D) x + 13 = 27
Solution:
(D)
Let the number be x.
According to the question, x + 13 = 27
Directions: In questions 24 to 40, fill in the blanks to make the statements true.
Question 24.
The distance (in km) travelled in h hours at a constant speed of 40 km per hour is ___.
Solution:
40 h
Distance = Speed × Time
= (40 × h) km = 40h km
Question 25.
p kg of potatoes are bought for Rs. 70. Cost of 1 kg of potatoes (in Rs.) is ____ .
Solution:
\(\frac{70}{p}\)
The cost of p kg of potatoes = Rs. 70
∴ The cost of 1 kg of potatoes \(=\mathrm{Rs} \cdot \frac{70}{p}\)
Question 26.
An auto rickshaw charges Rs. 10 for the first kilometre then Rs. 8 for each such subsequent kilometre. The total charge (in Rs.) for d kilometres is ____ .
Solution:
2 + 8d
For the first kilometre, rickshaw charges = Rs. 10.
And the charges for subsequent kilometre = Rs. 8.
∴ The charges for d kilometres
= 10 + (d – 1)8
= 10 + 8d – 8 = 2 + 8d
Question 27.
If 7x + 4 = 25, then the value of x is ___.
Solution:
3
We have given, 7x + 4 = 25
⇒ 7x + 4 – 4 = 25 – 4
[Subtracting 4 from both sides]
⇒ 7x = 21
⇒ \(\frac{7 x}{7}=\frac{21}{7}\)
[Dividing both sides by 7]
⇒ x = 3
Question 28.
The solution of the equation 3x + 7 = -20 is ____.
Solution:
-9
We have, 3x + 7 = – 20
⇒ 3x + 7 – 7 = -20 – 7
[Subtracting 7 from both sides]
⇒ 3x = -27
⇒ \(\frac{3 x}{3}=\frac{-27}{3}\)
[Dividing both sides by 3]
⇒ x = – 9
Question 29.
x exceeds y by 7′ can be expressed as ___.
Solution:
x = y + 7
x exceeds y by 7 can be expressed as x = y + 7 or x – y = 7.
Question 30.
8 more than three times the number x’ can be written as ___.
Solution:
3x + 8
8 more than three times the number x can be expressed as 3x + 8
Question 31.
Number of pencils bought for Rs. x at the rate of Rs. 2 per pencil is ___.
Solution:
\(\frac{x}{2}\)
Number of pencils bought for Rs. 2 = 1
∴ Number of pencils bought for Rs. x
\(=\frac{1}{2} \times x=\frac{x}{2}\)
Question 32.
The number of days in w weeks is ___.
Solution:
7w
Number of days in a week = 7
∴ Number of days in w weeks
= 7 × w = 7w
Question 33.
Annual salary at r rupees per month along with a festival bonus of Rs. 2000 is ____.
Solution:
Rs. (12r + 2000)
We have given, monthly salary = Rs. r
∴ Annual salary = Rs. (12 × r) = Rs. 12r
Now, total annual salary with a festive bonus = Rs. (12r + 2000)
Question 34.
The two digit number whose ten’s digit is ‘t’ and unit’s digit is ‘u’ is ___.
Solution:
10t + u
The digit at unit’s place is ‘u’. And the digit at ten’s place is ‘t’.
∴ The number can be expressed as 10 × t + u = 10t + u.
Question 35.
The variable used in the equation 2p + 8 = 18 is ___.
Solution:
p
p is the variable in the equation 2p + 8 = 18
Question 36.
x metres = ___ centimetres
Solution:
100x
1 metre = 100 cm
⇒ x metres = 100x cm
Question 37.
p litres = ___ millilitres
Solution:
1000p
1 litre = 1000 millilitres
⇒ p litres = 1000p millilitres
Question 38.
r rupees = ___ paise
Solution:
100r
1 rupee = 100 paise
⇒ r rupees = 100r paise
Question 39.
If the present age of Ramandeep is n years, then her age after 7 years will be ___.
Solution:
(n + 7) years
Present age of Ramandeep = n years
∴ Her age after 7 years = (n + 7) years.
Question 40.
If I spend f rupees from 100 rupees, the money left with me ___ is rupees.
Solution:
100 – f
I have 100 rupees and spend f rupees.
∴ Money left with me = (100 – f) rupees.
Directions: In questions 41 to 55, state whether the statements are true or false.
Question 41.
0 is a solution of the equation x + 1 = 0
Solution:
False
We have given, x + 1 = 0
⇒ x + 1 – 1 = 0 – 1
[Subtracting 1 from both sides]
⇒ x = – 1, which is the solution of the given equation.
Question 42.
The equation x + 1 = 0 and 2x + 2 = 0 have the same solution.
Solution:
True
We have given, x + 1 = 0
⇒ x + 1 – 1 = 0 – 1
[Subtracting 1 from both sides] …… (i)
⇒ x = -1
and 2x + 2 = 0
⇒ 2x + 2 – 2 = 0 – 2
[Subtracting 2 from both sides]
⇒ 2x = -2
\(\Rightarrow \frac{2 x}{2}=\frac{-2}{2}\)
[Dividing both sides by 2]
⇒ x = -1 …… (ii)
Thus, (i) and (ii) imply that both equations have the same solution.
Question 43.
If m is a whole number, then 2m denotes a multiple of 2.
Solution:
True
Question 44.
The additive inverse of an integer x is 2x.
Solution:
False
Since, additive inverse of x is -x.
Question 45.
If x is a negative integer, – x is a positive integer.
Solution:
True
Negative of a negative integer is always a positive integer.
Question 46.
2x – 5 > 11 is an equation.
Solution:
False
Since, an equation includes a sign of equality (=).
Question 47.
In an equation, the LHS is equal to the RHS.
Solution:
True
Question 48.
In the equation 7k – 7 = 7, the variable is 7.
Solution:
False
Since, in the equation 7k – 7 = 7, the variable is k.
Question 49.
a = 3 is a solution of the equation 2a – 1 = 5
Solution:
True
We have, 2a – 1 = 5
⇒ 2a – 1 + 1 = 5 + 1
[Adding 1 to both sides]
⇒ 2a = 6
⇒ \(\frac{2 a}{2}=\frac{6}{2}\) [Dividing both sides by 2]
⇒ a = 3, which is the solution of the given equation.
Question 50.
The distance between New Delhi and Bhopal is not a variable.
Solution:
True
Question 51.
t minutes are equal to 60t seconds.
Solution:
True
Since, 1 minute = 60 seconds
∴ t minutes = 60 × t seconds = 60t seconds
Question 52.
x = 5 is the solution of the equation 3x + 2 = 20
Solution:
False
We have, 3x + 2 = 20
⇒ 3x + 2 – 2 = 20 – 2
[Subtracting 2 from both sides]
⇒ 3x = 18
⇒ \(\frac{3 x}{3}=\frac{18}{3}\) [Dividing both sides by 3]
⇒ x = 6, which is the solution of the given equation.
Question 53.
One third of a number added to itself gives 8′, can be expressed as \(\frac{x}{3}+8=x\)
Solution:
False
Let the number be x.
One third of the number \(=\frac{x}{3}\).
According to the given question,
\(\frac{x}{3}+x=8\)
Question 54.
The difference between the ages of two sisters Leela and Yamini is a variable.
Solution:
False
The difference between the ages of two sisters will be a fixed number.
Question 55.
The number of lines that can be drawn through a point is a variable.
Solution:
False
Directions: In questions 56 to 74, choose a letter x, y, z, p etc , wherever necessary, for the unknown (variable) and write the corresponding expressions.
Question 56.
One more than twice the number.
Solution:
Let the number be x.
Twice of the number = 2x.
Now, 1 more than 2x can be expressed as 2x + 1.
Question 57.
20°C less than the present temperature.
Solution:
Let the present temperature be t° C.
Now, 20°C, less than t = (t – 20)°C
Question 58.
The successor of an integer.
Solution:
Let the integer be n.
Now, successor of the integer n = n + 1.
Question 59.
The perimeter of an equilateral triangle, if side of the triangle is m.
Solution:
We have given, side of the equilateral triangle = m.
The perimeter of an equilateral triangle = 3 × side = 3 m
Question 60.
Area of the rectangle with length k units and breadth n units.
Solution:
We have given, a rectangle of length = k units and breadth = n units.
Area of the rectangle = length × breadth
= (k × n) sq units = kn sq units
Question 61.
Omar helps his mother 1 hour more than his sister does.
Solution:
Let Omar’s sister helps her mother for x hours.
∴ Omar helps his mother for (x + 1) hours.
Question 62.
Two consecutive odd integers.
Solution:
Two consecutive odd integers are (2n + 1) and (2n + 3), where n is any integer.
Question 63.
Two consecutive even integers.
Solution:
Two consecutive even integers are 2m and 2m + 2, where m is any integer.
Question 64.
Multiple of 5.
Solution:
Multiple of 5 can be expressed as 5n, where n is an integer.
Question 65.
The denominator of a fraction is 1 more than its numerator.
Solution:
Let the numerator of the fraction be x.
∴ The denominator of the fraction can be expressed as x + 1.
∴ The fraction \(=\frac{x}{x+1}\) .
Question 66.
The height of Mount Everest is 20 times the height of Empire State building.
Solution:
Let the height of Empire State building be y.
∴ Height of Mount Everest = 20y.
Question 67.
If a note book costs Rs. p and a pencil costs Rs. 3, then the total cost (in Rs.) of two note books and one pencil.
Solution:
Cost of a notebook = Rs. p
Cost of 2 notebooks = Rs. 2p.
Cost of a pencil = Rs. 3.
∴ Cost of two notebooks and one pencil = Rs. (2p + 3)
Question 68.
z is multiplied by -3 and the result is subtracted from 13.
Solution:
z multiplied by -3 = -3z
– 3z subtracted from 13 = 13 – (-3z) = 13 + 3z
Question 69.
p is divided by 11 and the result is added to 10.
Solution:
p divided by 11 \(=\frac{p}{11}\).
\(\frac{p}{11}\) added to 10 = \(\frac{p}{11}\) + 10
Question 70.
x times of 3 is added to the smallest natural number.
Solution:
x times of 3 = 3x
And smallest natural number = 1.
So, 3x added to 1 = 3x + 1.
Question 71.
6 times q is subtracted from the smallest two digit number.
Solution:
6 times q = 6q.
The smallest two digit number = 10
6q subtracted from 10 = 10 – 6q.
Question 72.
Write two equations for which 2 is the solution.
Solution:
The required equations are 3y + 4 = 10 and 2x – 3 = 1, i.e., for both equations 2 is the solution.
Question 73.
Write an equation for which 0 is a solution.
Solution:
The required equation is 2t + 3 = 3, which has solution t = 0.
Question 74.
Write an equation whose solution is not a whole number.
Solution:
The required equation is x + 1 = 0, its solution is x = -1, which is not a whole number.
Directions: In questions 75 to 84, change the statements, converting expressions into statement in ordinary language.
Question 75.
A pencil costs Rs. p and a pen costs Rs. 5p.
Solution:
A pen costs 5 times the cost of a pencil.
Question 76.
Leela contributed Rs. y towards the Prime Minister’s Relief Fund. Leela is now left with Rs.(y + 10000).
Solution:
Amount left with Leela is Rs. 10,000 more than the amount she contributed towards the Prime Minister’s Relief Fund.
Question 77.
Kartik is n years old. His father is 7n years old.
Solution:
Age of Kartik’s father is seven times the age of Kartik.
Question 78.
The maximum temperature on a day in Delhi was p°C. The minimum temperature was (p – 10)°C.
Solution:
The minimum temperature on a day in Delhi was 10°C less than the maximum temperature.
Question 79.
John planted t plants last year. His friend Jay planted 2t + 10 plants that year.
Solution:
Last year Jay planted 10 more plants than twice the plants planted by his friend John.
Question 80.
Sharad used to take p cups tea a day. After having some health problem, he takes p – 5 cups of tea a day.
Solution:
Sharad reduced the consumption of tea per day by 5 cups after having some health problem.
Question 81.
The number of students dropping out of school last year was m. Number of students dropping out of school this year is m – 30.
Solution:
The number of students dropping out this year is 30 less than the number of students dropped out last year.
Question 82.
Price of petrol was Rs. p per litre last month. Price of petrol now is Rs. (p – 5) per litre.
Solution:
The price of petrol per litre decreased this month by Rs. 5 than its price last month.
Question 83.
Khader’s monthly salary was Rs. P in the year 2005. His salary in 2006 was Rs. (P + 1000).
Solution:
Khader’s monthly salary increased by Rs. 1000 in the year 2006 than that of 2005.
Question 84.
The number of girls enrolled in a school last year was q. The number of girls enrolled this year in the school is 3g – 10.
Solution:
The number of girls enrolled this year is 10 less than 3 times the girls enrolled last year.
Question 85.
Translate each of the following statements into an equation, using x as the variable:
(a) 13 subtracted from twice a number gives 3.
(b) One fifth of a number is 5 less than that number.
(c) Two – third of number is 12.
(d) 9 added to twice a number gives 13.
(e) 1 subtracted from one-third of a number gives 1.
Solution:
(a) Let the number be x.
Twice of the number x = 2x
According to question, 2x – 13 = 3
(b) Let the number be x.
One fifth of the number \(x=\frac{x}{5}\).
5 less than the number x = x – 5
According to question, \(\frac{x}{5}=x-5\)
(c) Let the number be x.
Two-third of the number x \(=\frac{2}{3} x\)
According to question, \(\frac{2}{3} x=12\)
(d) Let the number be x.
Twice of the number x = 2x.
Now, 9 is added to 2x = 9 + 2x
According to question, 9 + 2x = 13.
(e) Let the number be x.
One-third of the number \(x=\frac{x}{3}\).
Now, 1 is subtracted from \(\frac{x}{3}=\frac{x}{3}-1\)
According to question, \(\frac{x}{3}-1=1\)
Question 86.
Translate each of the following statements into an equation:
(a) The perimeter (p) of an equilateral triangle is three times of its side (a).
(b) The diameter (d) of a circle is twice its radius (r).
(c) The selling price (s) of an item is equal to the sum of the cost price (c) of an item and the profit (p) earned.
(d) Amount (a) is equal to the sum of principal (p) and interest (i).
Solution:
(a) We have given,
Perimeter of an equilateral triangle = 3 (the side of an equilateral triangle)
⇒ p = 3a
(b) We have given,
Diameter of a circle
= 2 (the radius of the circle)
⇒ d = 2r
(c) We have given,
Selling price = cost price + profit
⇒ s = c + p
(d) We have given,
Amount = principal + interest
⇒ a = p + i
Question 87.
Let Kanika’s present age be x years. Complete the following table, showing ages of her relatives :
A class with p students has planned a picnic. Rs. (iii) Her mother’s age = (x + 35 – 3) years = (x + 32) years
| Situation (described in ordinary language) | Expressions |
| (i) Her brother is 2 years younger. | ________ |
| (ii) Her father’s age exceeds her age by 35 years | ________ |
| (iii) Mother’s age is 3 years less than that of her father. | _________ |
| (iv) Her grandfather’s age is 8 times of her age | _________ |
Solution:
We have given, the present age of Kanika = x years.
(i) Her brother’s age = (x – 2) years
(ii) Her father’s age = (x + 35) years
(iii) Her mother’s age = (x + 35 – 3) years = (x + 32) years
(iv) Her grandfather’s age = 8x years
Question 88.
If m is a whole number less than 5, complete the table and by inspection of the table, find the solution of the equation 2m – 5 = -1 :
| m | |||||
| 2m – 5 |
For m = 0,
2m – 5 = 2 × 0 – 5 = 0 – 5 = -5
For m = 1,
2m – 5 = 2 × 1 – 5 = 2 – 5 = -3
For m = 2,
2m – 5 = 2 × 2 – 5 = 4 – 5 = – 1
For m = 3,
2m – 5 = 2 × 3 – 5 = 6 – 5 = 1
For m = 4
2m – 5 = 2 × 4 – 5 = 8 – 5 = 3
| m | 0 | 1 | 2 | 3 | 4 |
| 2m – 5 | -5 | -3 | -1 | 1 | 3 |
Thus, the solution of the equation 2m – 5 = -1 is m = 2.
Question 89.
A class with p students has planned a picnic. Rs. 50 per student is collected, out of which Rs. 1800 is paid in advance for transport. How much money is left with them to spend on other items?
Solution:
Number of students in the class = p
Total amount collected from p students = Rs. 50p
Amount paid in advance for transport = Rs. 1800
∴ Amount left with them = Rs. (50p – 1800)
Question 90.
In a village, there are 8 water tanks to collect rain water. On a particular day, x litres of rain water is collected per tank. If 100 litres of water was already there in one of the tanks, what is the total amount of water in the tanks on that day?
Solution:
Number of water tanks = 8
Rain water collected by each tank = x litres
∴ Rain water collected by 8 tanks = 8x litres
But 100 litres of water was already there in one of the tanks.
∴ Total amount of water in the tanks = (8x + 100) litres.
Question 91.
What is the area of square whose side is m cm?
Solution:
We have given, side of a square = m cm
Area of the square = side × side = m × m sq cm
Question 92.
Perimeter of a triangle is found by using the formula P = a + b + c, where a, b and c are the sides of the triangle. Write the rule that is expressed by this formula in words.
Solution:
Perimeter of a triangle is the sum of all its sides.
Question 93.
Perimeter of a rectangle is found by using the formula P = 2 (l + w), where l and w are respectively the length and breadth of the rectangle. Write the rule that is expressed by this formula in words.
Solution:
Perimeter of a rectangle is twice the sum of its length and breadth.
Question 94.
On my last birthday, I weighed 40 kg. If I put on m kg of weight after a year, what is my present weight?
Solution:
Present weight = weight on last birthday + weight put on after a year
= 40 kg + m kg
= (40 + m) kg
Question 95.
Length and breadth of a bulletin board are r cm and t cm, respectively.
(i) What will be the length (in cm) of the aluminium strip required to frame the board, if 10 cm extra strip is required to fix it properly.
(ii) If x nails are used to repair one board, how many nails will be required to repair 15 such boards?
(iii) If 500 sq cm extra cloth per board is required to cover the edges, what will be the total area of the cloth required to cover 8 such boards?
(iv) What will be the expenditure for making 23 boards if the carpenter charges Rs. x per board.
Solution:
We have given, length of the board = r cm and breadth = t cm.
(i) The length of aluminium strip to frame the board = Perimeter of the board
= 2(length + breadth)
= 2(r + t) cm
But 10 cm extra strip is required to fix it properly.
∴ Total length of the aluminium strip = 2(r + t) cm + 10 cm.
(ii) Number of nails required to repair 1 board = x.
∴ Number of nails required to repair 15 boards = 15 × x = 15x.
(iii) Area of the cloth required for 1 board = Area of the board
= length × breadth
= r cm × t cm
= (rt) sq cm
Area of the cloth required for 8 boards
= 8 × (rt) sq cm
= 8rt sq cm
But 500 sq cm extra cloth per board is required to cover the edges.
∴ For 8 boards we need 8 × 500 sq cm
= 4000 sq cm extra cloth.
Thus, the total area of the cloth required
= (8rt + 4000) sq cm
(iv) The carpenter charges for 1 board = Rs. x.
∴ The carpenter charges for 23 boards
= Rs. (23 × x) = Rs. 23x
Question 96.
Sunita is half the age of her mother Geeta. Find their ages
(i) after 4 years.
(ii) before 3 years.
Solution:
Let the present age of Sunita be x years.
The present age of her mother Geeta = 2(Sunita’s present age) = 2x years.
(i) After 4 years,
Sunita’s age = (x + 4) years
Geeta’s age = (2x + 4) years
Before 3 years,
Sunita’s age = (x – 3) years
Geeta’s age = (2x – 3) years.
Question 97.
Match the items of Column I with that of Column II:

Solution:
(i) ➝ (B), (ii) ➝ (E), (iii) ➝ (C), (iv) ➝ (C), (v) ➝(A)
(i) The number of corners of a quadrilateral is 4, i.e., a constant.
(ii) The variable in the equation 2p + 3 = 5 is p.
(iii) We have given, x + 2 = 3
⇒ x + 2 – 2 = 3 – 2
[Subtracting 2 from both sides]
⇒ x = 1, which is the solution of the given equation.
(iv) We have given, 2p + 3 = 5
⇒ 2p + 3- 3 = 5- 3
[Subtracting 3 from both sides]
⇒ 2p = 2
⇒ \(\frac{2 p}{2}=\frac{2}{2}\)
[Dividing both sides by 2]
⇒ p = 1, which is the solution of the given equation.
(v) Equality sign (=) is used in an equation.
We hope the NCERT Exemplar Class 6 Maths Chapter 7 Algebra will help you. If you have any query regarding NCERT Exemplar Class 6 Maths Chapter 7 Algebra, drop a comment below and we will get back to you at the earliest.