Important Questions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Class 12 Important Questions

Important Questions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Class 12 Important Questions

Electrostatic Potential and Capacitance Class 12 Important Questions Very Short Answer Type

Question 1.
A 500 µC charge is at the centre of a square of side 10 cm. Find the work done in moving a charge of 10 µC between two diagonally opposite points on the square. (Delhi 2008)
Answer:
The work done in moving a charge of 10 µC between two diagonally opposite points on the square will be zero because these two points will be at equipotential.

Question 2.
What is the electrostatic potential due to an electric dipole at an equatorial point? (All India 2009)
Answer:
Electric potential at any point in the equatorial plane of dipole is Zero.

Question 3.
What is the work done in moving a test charge q through a distance of 1 cm along the equatorial axis of an electric dipole? (All India 2009)
Answer:
Since potential for equatorial axis
V = 0
∴ W = qV = 0

Question 4.
Define the term ‘potential energy’ of charge ‘q’ at a distance V in an external electric field. (All India 2009)
Answer:
It is defined as the amount of work done in bringing the charge from infinity to its position in the system in the electric field of another charge without acceleration.
V = Er.

Question 5.
A point charge Q is placed at point O as shown in the figure. Is the potential difference V_A – V_B positive, negative or zero, if Q is
(i) positive
(ii) negative? (Delhi 2011)

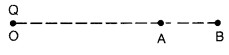
Answer:
Clearly,

As OA < OB, so the quantity within bracket is negative.
(i) If q is positive charge, V_A – V_B = negative
(ii) If q is negative charge, V_A – V_B = positive

Question 6.
A hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10 V. What is the potential at the centre of the sphere?
(All India 2011)
Answer:
The electric field inside the shell is zero. This implies that potential is constant inside the shell (as no work is done in moving a charge inside the shell) and, therefore, equals its value at the surface, which is 10 V.

Question 7.
A hollow metal sphere of radius 10 cm is charged such that the potential on its surface is 5 V. What is the potential at the centre of the sphere? (All India 2011)
Answer:
Hollow metal sphere behaves as an equipotential surface, so the potential at its centre will be 5 V.

Question 8.
Why is electrostatic potential constant throughout the volume of the conductor and has the same value (as inside) on its surface? (Delhi 2012)
Answer:
Electric field inside the conductor = 0

Question 9.
Distinguish between tor. dielectric and a conductor (Comptt. Delhi 2012)
Answer:

Dielectric	Conductor
Dielectrics are the in­sulating      materials which transmit electric effects without con­ducting.	Conductors are the sub­stances which can be used to carry or conduct electric charge from one place to the other.

Question 10.
Why must the electrostatic potential inside a hollow charged conductor be the same at every point? (Comptt. All India 2012)
Answer:
Inside the hollow charged conductor, electric field is zero therefore no work is done in moving a small test charge within the conductor. Hence electrostatic potential inside a hollow charged conductor is same at every point.

Question 11.
What is the geometrical shape of equipotential surfaces due to a single isolated charge? (Delhi 2013)
Answer:
Concentric spheres with a gap between them not being uniform as V \(\propto \frac{1}{r}\)

Question 12.
Two charges 2µC and – 2µC are placed at points A and B 5 cm apart. Depict an equipotential surface of the system. (Comptt. Delhi 2013)
Answer:

Question 13.
What is the amount of work done in moving a point charge around a circular arc of radius r at the centre of which another point charge is located? (Comptt. All India 2013)
Answer:
Being an equipotential surface, work done will be zero.

Question 14.
Two charges 4µC and -4µC are placed at points A and B 3 cm apart. Depict an equipotential surface of the system. (Comptt. All India 2013)
Answer:

Question 15.
“For any charge configuration, equipotential surface through a point is normal to the electric field.” Justify. (Delhi 2014)
Answer:
Work done in moving a charge over an equipotential surface is zero, hence a point on it will be normal to the electric field.
W = FS cos θ ∴ cos θ = 0 or θ = 90o

Question 16.
Two equal balls having equal positive charge ‘q’ coulumbs are suspended by two insulating strings of equal length. What would be the effect on the force when a plastic sheet is inserted between the two ? (All India 2014)
Answer:
The force would be reduced by a factor ‘K’ (equal to the value of dielectric constant of plastic sheet)

Question 17.
The given graph shows variation of charge ‘q’ versus potential difference ‘V’ for two capacitors C₁ and C₂. Both the capacitors have same plate seperation but plate area of C₂ is greater than that of C₁. Which line (A or B) corresponds to C₁ and why? (Comptt. All India 2014)

Answer:
Line B corresponds to C₁
Reason: Since slope \(\left(\frac{q}{v}\right)\) of ‘B’ is less than that of ‘A’

Question 18.
A charge ‘q’ is moved from a point A above a dipole of dipole movement ‘p’ to a point B below the dipole in equitorial plane without acceleration. Find the work done in the process. (All India 2016)

Answer:
No work is done
[W = q V_AB = q × 0 = 0, since potential remains constant]

Electrostatic Potential and Capacitance Class 12 Important Questions Short Answer Type

Question 19.
Derive the expression for the electric potential at any point along the axial line of an electric dipole (Delhi 2008)
Answer:
Consider an electric dipole consisting of two points charged -q and +q and seperated by distance 2a. Let P be a point on the axis of the dipole at a distance r from its centre O.

Electric potential at point P due to dipole is,
V = V₁ + V₂

Question 20.
Derive an expression for the potential energy of an electric dipole of dipole movement \(\vec{p}\) in the electric field \(\vec{E}\)
(Delhi 2008)
Answer:
Consider a dipole with charges +q and -q placed in a uniform electric field \(\overrightarrow{\mathrm{E}}\) such that AB = 2a as shown in the figure

Since the dipole experiences no net force in a uniform electric field but experiences a torque (τ) is given by

It tends to rotate the dipole in clockwise direction. To rotate the dipole anti-clock wise has to be done on the dipole.

Question 21.
Two point charges, q₁ = 10 × 10^-8C, q₂ = -2 × 10^-8C are seperated by a distance of 60 cm in air.
(i) Find at what distance from the 1^st charge, q₁ would the electric potential be zero.
(ii) Also calculate the electrostatic potential energy of the system. (All India 2008)
Answer:
(i) Given : q₁ = 10 × 10^-8C, q₂ = -2 × 10^-8C
AB = 60 cm = 0.60 = 0.6m
Let AP = x

∴ Distance from first charge = 0.5 m = 50 cm.
(ii) Electrostatic energy of the system is

Question 22.
Two point charges 4Q, Q are separated by lm in air. At what point on the line joining the charges is the electric field intensity zero?
Also calculate the electrostatic potential energy of the system of charges, taking the value of charge, Q = 2 × 10^-7C
Answer:

(ii) Electrostatic potential energy of the system is

Question 23.
Two point charges 20 x 10-6 C and -4 X 10-6 C are separated by a distance of 50 cm in air.
(i) Find the point on the line joining the charges, where the electric potential is zero.
(ii) Also find the electrostatic potential energy of the system. (All India 2008)
Answer:
(i) Here q₁ = 20 × 10^-6C, q₂ = -4 × 10^-6C
and AB = 50 cm = 0.50 m = 0.5 m Let AP = x then PB = 0.5 – x
Potential at P due to charge q₁ = \(\frac{\mathrm{K} q_{1}}{\mathrm{AP}}\)
Potential at P due to charge q₂ = \(\frac{\mathrm{K} q_{2}}{\mathrm{PB}}\)
Potential at P = 0 \(\Rightarrow \frac{\mathrm{K} q_{1}}{\mathrm{AP}}+\frac{\mathrm{K} q_{2}}{\mathrm{PB}}=0\)

Question 24.
Calculate the work done to dissociate the system of three charges placed on the vertices of a triangle as shown. (Delhi 2008)

Answer:
Initial P.E. of the three charges

Final P.E, u_f = 0
∴ Work required to dissociate the system of three charges,
W = u_f – u_i = -2.304 × 10^-8 J

Question 25.
(i) Can two equipotential surfaces intersect each other? Give reasons.
(ii) Two charges -q and + q are located at points A (0, 0, – a) and B (0, 0, +a) respectively. How much work is done in moving a test charge from point P (7, 0, 0) to Q (-3,0,0)? (Delhi 2009)
Answer:
(i) No, if they intersect, there will be two different directions of electric field at that point which is not correct. If they intersect, then at the same point of intersection, there will be two values of potential. This is not possible and hence two equipotential surfaces cannot intersect.
(ii) Since both the points P and Q are on the equatorial line of the dipole and V = 0 at every point on it, work done will be zero. Also the force on any charge is perpendicular to the equatorial line, so work done is zero.

Question 26.
Draw 3 equipotential surfaces corresponding to a field that uniformly increases in magnitude but remains constant along Z-direction. How are these surfaces different from that of a constant electric field along Z-direction? (All India 2009)
Answer:
d₂ < d₁ for increasing field
and d₂ = d₁ for uniform field.

Question 27.
Two uniformly large parallel thin plates having charge densities + σ and – σ are kept in the X-Z plane at a distance ‘d’ apart. Sketch an equipotential surface due to electric field between the plates. If a particle of mass m and charge q’ remains stationary between the plates, what is the magnitude and direction of this field? (Delhi 2011)
Answer:
The equipotential surface is at a distance d/2 from either plate in X-Z plane. For a particle of charge (- q) at rest between the plates, then

(i) weight mg acts, vertically downward
(ii) electric force qE acts vertically upward
so mg = qE
E = \(\frac{m g}{q}\) vertically downward,
i.e., along (-) Y-axis.

Question 28.
Two small identical electrical dipoles AB and CD, each of dipole moment ‘p’ are kept at an angle of 120° as shown in the figure. What X’ is the resultant dipole moment of this combination? If this system is subjected to electric field (\(\overrightarrow{\mathbf{E}}\)) directed along + X direction, what will be the magnitude and direction of the torque acting on this? (Delhi 2011)

Answer:
Resultant dipole moment of both dipoles is

Resultant dipole moment (p) makes an angle of 60° with each dipole and 30° with x-axis as shown in the figure.

Question 29.
Figure shows two identical capacitors C₁ and C₂, each of 2 µF capacitance, connected to a battery of 5 V. Initially switch ‘S’ is left open and dielectric slabs of dielectric constant K = 5 are inserted to fill completely the space between the plates of the two capacitors. How will the charge and

(ii) potential difference between the plates of the capacitors be affected after the slabs are inserted? (Delhi 2011)
Answer:
(i) When switch S is open and dielectric is introduced, charge on each capacitor will be q₁ = C₁ V, q₂ = C₂V
q₁ = 5CV
= 5 × 2 × 5 = 50 µC, q₂ = 50 µC
Charge on each capacitor will become 5 times
(ii) P.d. across C₁ is still 5V and across C₂,
q = (5C) V

Question 30.
Figure shows two identical capacitors C¹ and C² each of 1.5 µF capacitance, connected to a battery of 2 V. Initially switch ‘S’ is closed. After sometime ‘S’ is left open and dielectric slabs of dielectric constant K = 2 are inserted to fill completely the space between the plates of the two capacitors. How will the
(i) charge and
(ii) potential difference between the plates of the capacitors be affected after the slabs are inserted? (Delhi)

Answer:
(i) When switch S is open and dielectric is introduced, charge on each capacitor, will be
q₁ = C₁V,
q₂ = C₂V,
q₁ = 2CV = 2 × 1.5 × 2 = 6 µC, q₂ = 6 µC
Charge on each capacitor will become twice.
(ii) P.d. across C₁ is still 2V and across C₂,
q = (2C) V’

Question 31.
Net capacitance of three identical capacitors in series is 1 pF. What will be their net capacitance if connected in parallel?
Find the ratio of energy stored in the two configurations if they are both connected to the same source. (All India 2011)
Answer:
Let C be the capacitance of a capacitor
Given : C₁ = C₂ = C₃ = C When connected in series:

Question 32.
Net capacitance of three identical capacitors in series is 3 pF. What will be their net capacitance if connected in parallel?
Find the ratio of energy stored in the two configurations if they are both connected to the same source. (All India 2011)
Answer:
Let C₁, C₂ and C₃ be the capacitances of three capacitors. But these three capacitors are of same capacitance, so C is the capacitance of each capacitor.

Question 33.
Draw a plot showing the variation of
(i) electric field (E) and
(ii) electric potential
(iii) with distance r due to a point charge Q. (Delhi 2012)
Answer:

Question 34.
A test charge ‘q’ is moved without acceleration from A to C along the path from A to B and then from B to C in electric field E as shown in the figure.

(i) Calculate the potential difference between A and C.
(ii) At which point (of the two) is the electric potential more and why? (All India)
Answer:
(i) P.D does not depend upon the path along which the test charge q moves

(ii) At point C, electric potential will be more as potential decreases in the direction of electric field.

Question 35.
An electric dipole is held in a uniform electric field.
(i) Show that the net force acting on it is zero.
(ii) The dipole is alligned parallel to the field.
Find the work done in rotating it through the angle of 180°. (All India 2012)
Answer:
(i) Force acting on point A due to charge -q is -qE
Force acting on point B due to charge +q. is + qE
Net force acting on
= -qE + qE = 0 (zero)

Hence, the net force acting on electric dipole held in a uniform electric field is zero.
(ii) W = -pE(cos 0₂ — cos θ₂)
W = -pE(cos 180° – cos 0°)
=> W = -pE(-1 – (1)) = +2pE

Question 36.
Determine the potential difference across the plates of the capacitor ‘C₁‘ of the network shown in the figure.

[Assume E₂ > E₁] (Comptt. Delhi 2012)
Answer:
Net E = E₂ – E₁
Both capacitors are in series

∴ V₁, (Potential difference across the plates of the capacitor C₁) = \(\frac{q}{C_{1}}\)

Question 37.
A network of four capacitors, each of capacitance 15 µF, is connected across a battery of 100 V, as shown in the figure. Find the net capacitance and the charge on the capacitor C₄. (Comptt. Delhi & All India 2012)
Answer:
C₁, C₂ and C₃ are in series as shown in the figure, we have

Question 38.
A network of four capacitors, each of capacitance 30 pF, is connected across a battery of 60 V as shown in the figure.
Find the net capacitance and the energy stored in each capacitor. (Comptt. All India 2012)

Answer:

Question 39.
An electric dipole of length 4 cm, when placed with its axis making an angle of 60° with a uniform electric field, experiences a torque of 4√3 Nm. Calculate the potential energy of the dipole, if it has charge ± 8 nC. (Delhi 2014)
Answer:
1^st method Given : 2a = 4 cm = 4 × 10^-2 m, θ = 60°
τ = 4 × √3 Nm, q = ±8 nC = ±8 x 10^-9 C
P.E. = |p| |E| cos θ, τ = |p| |E| sin θ

(Note: However, the first method is preferred because it saves a lot of time for unnecessary calculations)

Question 40.
An electric dipole of length 2 cm, when placed with its axis making an angle of 60° with a uniform electric field, experiences a torque of
8 √3 Nm. Calculate the potential energy of the dipole, if it has a charge of ± 4 nC. (Delhi 2014)
Answer:
1^st method Given : 2a = 4 cm = 4 × 10^-2 m, θ = 60°
τ = 4 × √3 Nm, q = ±8 nC = ±8 x 10^-9 C
P.E. = |p| |E| cos θ, τ = |p| |E| sin θ

(Note: However, the first method is preferred because it saves a lot of time for unnecessary calculations)
Answer:
8 Joules

Question 41.
An electric dipole of length 1 cm, which placed with its axis making an angle of 60° with uniform electric field, experiences a torque of
6√3 Nm. Calculate the potential energy of the dipole, if it has a charge of ± 2 nC. (Delhi 2014)
Answer:
1^st method Given : 2a = 4 cm = 4 × 10^-2 m, θ = 60°
τ = 4 × √3 Nm, q = ±8 nC = ±8 x 10^-9 C
P.E. = |p| |E| cos θ, τ = |p| |E| sin θ

(Note: However, the first method is preferred because it saves a lot of time for unnecessary calculations)
Answer: 6 Joules

Question 42.
A parallel plate capacitor of capacitance C is charged to a potential V. It is then connected to another uncharged capacitor having the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor. (All India 2014)
Answer:
Let us say that capacitor has an initial energy

When the first capacitor is connected across the second capacitor, let the common potential be V’

Then charge on each capacitor q’ = CV’
By charge conservation
q’ = \(\frac{q}{2}\)
Hence total energy stored in the capacitors,

Question 43.
Two point charges q₁ and q₂ are located at \(\overrightarrow{r_{1}}\) and \(\overrightarrow{r_{2}}\) respectively in an external electric field \(\overrightarrow{\mathbf{E}}\) .
Obtain the expression for the total work done in assembling this configuration. (Comptt. Delhi 2014)
Answer:
Work done in bringing the charge q₁ from infinity to position r₁
W₁ = q₁V(r₁)
Work done in bringing charge q₂ to the position r₂

Hence, total work done in assembling the two charges
w = W₁ + W₂

Question 44.
Two point charges q and -2q are kept ‘d’ distance apart. Find the location of the point relative to charge ‘q’ at which potential due to this system of charges is zero. (Comptt. Delhi 2014)
Answer:

At distance’d’ towards left of charge ‘q’

Question 45.
Two closely spaced equipotential surfaces A and B with potentials V and V + δV, (where δV is the change in V), are kept δl distance apart as shown in the figure.

Deduce the relation between the electric field and the potential gradient between them. Write the two important conclusions concerning the relation between the electric field and electric potentials.
(Comptt. Delhi 2014)
Answer:
Work done in moving a unit positive charge along distance δl

Two important conclusions :
(i) Electric field is in the direction in which the potential decreases steepest.
(ii) Magnitude of electric field is given by the change in the magnitude of potential per unit displacement, normal to the equipotential surface at the point.

Question 46.
Why does current in a steady state not flow in a capacitor connected across a battery? However momentary current does flow during charging or discharging of the capacitor. Explain. (All India 2017)
Answer:
In the steady state, the displacement current and hence the conduction current, is zero as | \(|\overrightarrow{\mathrm{E}}|\) | between the plates, is constant.

During charging and discharging, the displacement current and hence the conduction current is non zero as | \(|\overrightarrow{\mathrm{E}}|\) | between the plates, is changing with time.

Current is non zero as | \(|\overrightarrow{\mathrm{E}}|\) | between the plates, is changing with time.

Short Answer Type Questions-ll tSA-ll) (3 Marks)

Question 47.
Three identical capacitors C₁ C₂ and C₃ of capacitance 6 µF each are connected to a 12 V battery as shown.
Find
(i) charge on each capacitor
(ii) equivalent capacitance of the network
(iii) energy stored in the network of capacitors. (Delhi 2009)

Answer:
C₁ and C₂ in series, make C₄ = 3µF
using \(\frac{1}{\mathrm{C}_{4}}=\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}\)
(i) 12V of potential is available in C₄ and C₃.
Charge in C₃ = Q₃ = C₃V
= 6 × 10^-6 × 12 = 72 µC
Charge in C₄ = Q₄ = C₄V
= 3 × 10^-6 × 12 = 36 µC
∴ Charge on C₁ and C₂ will also be 36 μC
(ii) C₄ and C₃ are in parallel to the source
∴ C_eq = 3 + 6 = 9 μF
(iii) Energy stored = \(\frac{1}{2} \mathrm{C}_{\mathrm{eq}} \mathrm{V}^{2}\)

= 648 × 10^-6 = 6.48 × 10^-4 joule

Question 48.
The equivalent capacitance of the combination between A and B in the given figure is 4 μF.

(i) Calculate capacitance of the capacitor C.
(ii) Calculate charge on each capacitor if a 12 V battery is connected across terminals A and B.
(iii) What will be the potential drop across each capacitor? (Delhi 2009)
Answer:
C_eq = 4 μF
(i) Since 20 μF and C are in series, we have

(ii) Charge drawn from 12 V battery is Q
= C_eq.V = 4 × 12 = 48 μC
So charge on each capacitor = 48 pC
(iii) Potential drop across

Question 49.
Two parallel plate X and Y capacitors, X and Y, have the same area of plates and same separation between them. X has air between the plates while Y contains a dielectric medium of ε_r = 4.
(i) Calculate capacitance of each capacitor if equivalent capacitance of the combination is 4 μF.
(ii) Calculate the potential difference between the plates of X and Y.
(iii) What is the ratio of electrostatic energy stored in X and Y? (Delhi)
Answer:
Since area A and separation d are same, if C_x = C then C_y = 4C
(i) Since they are in series, \(\frac{1}{4}=\frac{1}{C}+\frac{1}{4 C}\)

The two capacitors are therefore 5 μF and 20 μF.
(ii) Since the capacitance of capacitors are in the ratio 1 : 4,
the potential drop across them should be in the ratio of 4 : 1 making them \(\left(4 \times \frac{12}{5}\right) \frac{12}{5}\)
(iii) Since they carry same charge, the ratio of the electrostatic energy is,

Question 50.
A parallel plate capacitor is charged by a battery. After some time the battery is disconnected and a dielectric slab of dielectric constant K is inserted between the plates. How would
(i) the capacitance,
(ii) the electric field between the plates and
(iii) the energy stored in the capacitor, be affected? Justify your answer. (All India 2009)
Answer:
Let C be the capacitance and V be the potential difference.
The charge on the capacitor plates will then be Q = CV.
The electric field between the plates, E = \(\frac{\mathrm{V}}{d}\) and the energy stored,

As the dielectric (K) is introduced after disconnecting the battery
We have the new values of charge, Q’ = Q Capacitance C’ = KC
Potential V’ = \(\frac{Q}{K C}=\frac{V}{K}\)
(i) New capacitance is K times its original.

Question 51.
(a) A charge +Q is placed on a large spherical conducting shell of radius R. Another small conducting sphere of radius r carrying charge ‘q’ is introduced inside the large shell and is placed at its centre. Find the potential difference between two points, one lying on the sphere and the other on the shell.
(b) How would the charge between the two flow if they are connected by a conducting wire? Name the device which works on this fact. (All India 2009)
Answer:
Potential inside conducting spherical shell of radius R carrying charge,
q = constant = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{R}\)
Let us suppose that in some way we introduce a small sphere of radius r, carrying charge q, into the large one, and place it at the centre.

The potential due to this new charge clearly has the following values at the radii indicated :
Potential due to small sphere of radius r carrying charge q

of radius R
Taking both charges q and Q into account, we have for the two potentials :

(b) If we connect the smaller and larger sphere by a wire, the charge will flow from the conducting sphere of radius r to the large spherical shell of radius R. Van de Graaff generator works on this fact.

Question 52.
A parallel plate capacitor is charged by a battery. After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates. How will
(i) the capacitance of the capacitor,
(ii) electric field between the plates and
(iii) the energy stored in the capacitor be affected? Justify your answer in each case.
Answer:
Let C be the capacitance and V be the potential difference.
The charge on the capacitor plates will then be Q = CV.
The electric field between the plates, E = \(\frac{\mathrm{V}}{d}\) and the energy stored,

As the dielectric (K) is introduced after disconnecting the battery
We have the new values of charge, Q’ = Q Capacitance C’ = KC
Potential V’ = \(\frac{Q}{K C}=\frac{V}{K}\)
(i) New capacitance is K times its original.

Question 53.
(a) Depict the equipotential surfaces for a system of two identical positive point charges placed a distance ‘d’ apart.
(b) Deduce the expression for the potential energy of a system of two point charges q₁ and q₂ brought from infinity to the points \(\overrightarrow{r_{1}}\)and \(\overrightarrow{r_{2}}\) respectively in the presence of external electric field \(\overrightarrow{\mathbf{E}}\). (Delhi 2010)
Answer:
(a)

Equipotential surfaces of two identical point charges
(b) Let \(\overrightarrow{\mathrm{E}}\) be the external field
∴ Work done on q₂ against the external field = q₂.V( \(\overrightarrow{r_{2}}\) )
Work done on q₂ against the field due to

..where [r₁₂ is the distance between q₁ and q₂
By the superposition principle for fields, we add up the work done on q₂ against the two fields (\(\overrightarrow{\mathrm{E}}\) and that due to q₁).

Thus, potential energy of the system = Total work done in assembling the configuration.

Question 54.
A parallel plate capacitor, each with plate area A. and separation d, is charged to a potential difference V. The battery used to charge it remains connected. A dielectric slab of thickness d and dielectric constant k is now placed between the plates. What change, if any, will take place in :
(i) charge on plates?
(ii) electric field intensity between the plates?
(iii) capacitance of the capacitor?
Justify your answer in each case. (Delhi 2010)
Answer:
Given : Plate area of either plate of parallel plate capacitor = A
Distance between the plates = d and
potential difference between the plates = V
∴ Initially capacitance, C = \(\frac{\varepsilon_{0} A}{d}\),
Charge on plate, Q = CV
As the battery remains connected throughout, the potential difference between the plates remains unchanged (V’ = V) on placing, a dielectric slab of thickness ‘d’ and dielectric constant ‘k’ between the plates.
(i) New charge on plates, Q’ = C’ V’ = kCV = kQ
Thus, charge changes to k times of its original value.
(ii) Electric field intensity between the plates, E’

Thus, electric field intensity between the plates of capacitor remains unchanged.
(iii) New capacitance of the capacitor,

Question 55.
A parallel plate capacitor is charged to a potential difference V by a d.c. source. The capacitor is then disconnected from the source. If the distance between the plates is doubled, state with reason how the following will change;
(i) electric field between the plates,
(ii) capacitance, and
(iii) energy stored in the capacitor. (Delhi 2010)
Answer:

On disconnecting the battery, the charge q on the capacitor plates remains unchanged.
If the distance d is doubled, then

Question 56.
A network of four capacitors each of 12μF capacitance is connected to a 500 V supply as shown in the figure.
Determine
(a) equivalent capacitance of the network and
(b) charge on each capacitor. (All India)

Answer:
(a) Equivalent capacitance of the network,

Question 57.
A network of four capacitors each of 15 μF capacitance is connected cf to a 500 V supply as shown in the figure.
Determine
(a) equivalent capacitance of the network and
(b) charge on each capacitor. (All India 2010)
Answer:

Now C_S and C₄ are in parallel
∴ Equivalent capacitance of the network,
C = C_S + C₄ = 15 + 5 = 20 μF
(b) Charge on capacitor, C₄ is
q = C₄V = (15 × 10^-6) × 500 = 7500 μC … [V =500
Charge on each capacitor, C₁, C₂ and C₃ will be, q = C_SV = (5 × 10^-6) × 500 = 2500 μC

Question 58.
Deduce the expression for the electrostatic energy stored in a capacitor of capacitance ‘C’ and having charge ‘Q’.
How will the
(i) energy stored and
(ii) the electric field inside the capacitor be affected when it is completely filled with a dielectric material of dielectric constant ‘K’? (All India 2012)
Answer:
Potential of capacitor = \(\frac{q}{C}\)
Small amount of work done in giving an additional charge dq to the capacitor,

Total work done in giving a charge Q to the capacitor

As electrostatic force is conservative, thus work is stored in the form of potential energy (U) of the capacitor.

∴ Electric field will become \(\frac{1}{\mathrm{K}}\) times its initial value.

Question 59.
A capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 360 μC. When potential across the capacitor is reduced by 120 V, the charge stored in it becomes 120 μC.
Calculate:
(i) The potential V and the unknown capacitance C.
(ii) What will be the charge stored in the
capacitor, if the voltage applied had increased by 120 V? (Delhi 2013)
Answer:
(i) Let the capacitance be C
∴ Charge on Q₁ = CV or 360 μC = CV …(i)
In second case,
Q₂ = C(V – 120)
⇒ 120 μC = C(V – 120) …(ii)
From equation (i) and (ii)

3V – 360 = V ⇒ 2V = 360
By putting this value of V in (ii)
120 × 10^-6 = C(180 – 120)

(ii) Charge stored when voltage is increased by 120 V
Q’ = 2μF × (180 + 120) V = 600 μC

Question 60.
A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness d/2, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.
(All India 2012)
Answer:
Total potential difference between the plates

Question 61.
Calculate the amount of work done to dissociate a system of three charges 1 μC, 1 μC and -4 μC placed on the vertices of an equilateral triangle of side 10 cm. (Comptt. All india)
Answer:


Hence, 0.63 Joules of energy is required to dissociate the system.

Question 62.
A capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 300 µC. When potential across the capacitor is reduced by 100 V, the charge stored in it becomes 100 V. Calculate the potential V and the unknown capacitance. What will be the charge stored in the capacitor if the voltage applied had increased by 100 V? (Delhi 2013)
Answer:
(i) Charge stored, Q = CV
300 µC = C × V ,
When potential is reduced by 100 V
100 µC = C(V – 100) = CV – 100 C
100 µC = 300 µC – 100 C
⇒ 100 C = 300 µC – 100 µC
⇒ 100 C = 200 µC
Therefore, capacitance C = 2µF

(ii) Charge stored when voltage applied is increased by 100 V
Q’ = 2µF × (150 + 100) = 500µC

Question 63.
Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero. (All India 2013)
Answer:
Potential at all points in equatorial plane is zero everywhere

Question 64.
Two thin concentric shells of radii r₁ and r₂ (r₂ > r₁) have charges q₁ and q₂. Write the expression for the potential at the surface of inner and outer shells. (Comptt. All India 2013)
Answer:
(i) Potential at the surface of inner shell,

(Since the charge on inner shell will also con-tribute)

Question 65.
(a) Obtain the expression for the energy stored per unit volume in a charged parallel plate capacitor.
(b) The electric field inside a parallel plate capacitor is E. Find the amount of work done in moving a charge q over a closed rectangular loop a b c d a.(Delhi 2013)

Answer:
(a) Energy of a parallel plate capacitor.

Potential of capacitor = \(\frac{q}{C}\)
Small amount of work done in giving an additional charge dq to the capacitor,

Total work done in giving a charge Q to the capacitor

As electrostatic force is conservative, thus work is stored in the form of potential energy (U) of the capacitor.

∴ Electric field will become \(\frac{1}{\mathrm{K}}\) times its initial value.

[Read answer only upto U = \(\frac{1}{2}\) CV²
(b) The amount of work done in moving a charge Y over a closed rectangular loop abcda is zero, because net displacement is zero.
W = q\(\overrightarrow{\mathrm{E}} \cdot \vec{d}\)

Question 66.
Derive the expression for the capacitance of a parallel plate capacitor having plate area A and plate separation d. (Delhi 2013)
Answer:
Capacity of a parallel plate capacitor. A parallel plate capacitor consists of two large plane parallel conducting plates separated by a small distance. We first take the intervening medium between the plates to be vaccum. Let A be the area of each plate and d the separation between them. The two plates have charges Q and – Q. Since d is much smaller than the linear dimension of the plates (d² << A), we can use the result on electric field by an infinite plane sheet of uniform surface charge density. Plate 1 has surface charge density σ = Q/A and Plate 2 has a surface charge density -σ, the electric field in different region is:

In the inner region between the plates 1 and 2, the electric fields due to the two charged plates add up, giving

The capacitance C of the parallel plate capacitor is then

Question 67.
Two parallel plate capacitors of capacitances C₁ and C₂ such that C₁ = 3C₂ are connected across a battery of V volts as shown in the figure. Initially the key (k) is kept dosed to fully charge the capacitors. The key is now thrown open and a dielectric slab of dielectric constant ‘K’ is inserted in the two capacitors to completely fill the gap between the plates,

Find the ratio of
(i) the net capacitance and
(ii) the energies stored in the combination, before and after the introduction of the dielectric slab. (Comptt. Delhi 2013)
Answer:
(i) Net capadtance before filling the gap with dielectric slab

Energy stored in the combination before introduction of dielectric slab,

Question 68.
Two parallel plate capacitors of capacitances C₁ and C₂ such that C₁ = 2C₂ are connected across a battery of V volts as shown in the figure. Initially the key (k) is kept closed to fully charge the capacitors. The key is now thrown open and a dielectric slab of dielectric constant ’K’ is inserted in the two capacitors to completely fill the gap between the plates.

Find the ratio of
(i) the net capacitance and
(ii) the energies stored in the combination, before and after the introduction of the dielectric slab. (Comptt. Delhi 2013)
Answer:
(i) Net capacitance before filling the gap with dielectric slab

(ii) Energy stored in the combination before introduction of dielectric slab

Energy stored in the combination after introduction of dielectric slab

Question 69.
Two parallel plate capacitors of capacitances C₁ and C₂ such that C₁ = (C₂)/2 are connected across a battery of V volts as shown in the figure. Initially the key (k) is kept closed to fully charge the capacitors. The key is now thrown open and a dielectric slab of dielectric constant ‘K’ is inserted in the two capacitors to completely fill the gap between the plates.

Find the ratio of
(i) the net capacitance and
(ii) the energies stored in the combination, before and after the introduction of the dielectric slab. (Comptt. Delhi 2013)
Answer:
(i) Net capacitance before filling the gap with dielectric slab

(ii) Energy stored in the combination before introduction of dielectric slab

Question 70.
Two capacitors of unknown capacitances C₁ and C₂ are connected first in series and then in parallel across a battery of 100 V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively, determine the value of C₁ and C₂. Also calculate the charge on each capacitor in parallel combination. (Delhi 2015)
Answer:
Energy stored in a capacitor is given by,

Question 71.
Calculate the potential difference and the energy stored in the capacitor C₂ in the circuit shown in the figure. Given potential at A is 90 V, C₁ = 20 µF, C₂ = 30 µF and C₃ = 15 µF. (All India 2015)

Answer:
Given V_A = 90 V, C₁ = 20 µF, C₂ = 30 µF and C₃ = 15 µF
Since these capacitors are connected in series, net capacitance (C) will be,

Question 72.
Two parallel plate capacitors X and Y have the same area of plates and same separation between them. X has air between the plates while Y contains a dielectric medium of \(\varepsilon_{r}\) = 4.

(i) Calculate capacitance of each capacitor if equivalent capacitance of the combination is 4 pF.
(ii) Calculate the potential difference between the plates of X and Y.
(iii) Estimate the ratio of electrostatic energy stored in X and Y. (Delhi 2015)
Answer:
(i) Let C_x = C

Question 73.
Define an equipotential surface. Draw equipotential surfaces :
(i) in the case of a single point charge and
(ii) in a constant electtic field in Z-direction. Why the equipotential surfaces about a single charge are not equidistant?
(iii) Can electric field exist tangential to an equipotential surface? Give reason. (All India 2015)
Answer:
A surface with a constant value of potential at all points of the surface is defined as ‘equipotential surface’ „
(i) Equipotential surface for a single point charge.

(ii) Equipotential surface in a constant electric field as shown in the adjoining diagram.
Equipotential surface are not equidistant, because V \(\propto \frac{1}{r}\)
(iii) No, If the field lines are tangential, work will be done in moving a charge on the surface which goes against the definition of equipotential surface.

Question 74.
A parallel plate capacitor, of capacitance 20pF, is conneted to a 100 V supply. After sometime the battery is disconnected, and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitor
(i) before
(ii) after the dielectric has been put in between its plates. (Comptt. Outside Delhi 2015)
Answer:

Question 75.
(i) Find equivalent capacitance between A and B in the combination given below. Each capacitor is of 2 µF capacitance

(ii) If a dc source of 7 V is connected across AB, how much charge is drawn from the source and what is the energy stored in the network? (Delhi 2015)
Answer:

Question 76.
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor? If another capacitor of 6 pF is connected in series with it with the same battery connected across the combination, find the charge stored and potential difference across each capacitor. (Delhi 2015)
Energy stored, in the capacitor of capacitance 12 pF,

∴ Charge stored across each capacitor
q = CV = (4 × 10^-12) × 50 C = 2 × 10^-10C
Charge on each capacitor 12 pF as well as on 6 pF is 2 × 10^-10 C
∴ Potential difference across capacitor C₁

Question 77.
(i) Derive the expression for the electric potential due to an electric dipole at a point on its axial line.
(ii) Depict the equipotential surfaces due to an electric dipole. (Delhi 2015)
Answer:
(i) The potential due to the dipole is the sum of potentials due to the charges q and – q

where r₁ and r₂ are the distances of the point P from q and – q, respectively.
Now, by geometry,

Using the Binomial theorem and retaining terms upto the first order in a/r; we obtain,

where \(\hat{\gamma}\) is the unit vector along the position vector OP.
The electric potential of a dipole is then given by

From the above equation (iv), potential on the dipole axis (θ = 0, n) is given by

(ii) Equipotential surface for an electric dipole

Question 78.
Two identical capacitors of 12 pF each are connected in series across a battery of 50 V. How much electrostatic energy is stored in the combination ? If these were connected in parallel across the same battery, how much energy will be stored in the combination now? Also find the charge drawn from the battery in each case. (Delhi 2015)
Answer:

Question 79.
Two identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant K. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.

Answer:


Question 80.
(a) Write two properties by which electric potential is related to the electric field.
(b) Two point charges q₁ and q₂, separated by a distance of r₁₂ are kept in an external electric field. Derive an expression for the potential energy of the system of two charges in the field. (Comptt. Delhi 2015)
Answer:
(a) Two properties which relate electric potential to electric field—
(i) Electric field is in the direction in which potential decreases at the maximum rate.
(ii) Magnitude of electric field is given by change in the magnitude of potential per unit displacement normal to a charged conducting surface, or E =
(b) Work done in bringing the charge q1 to a point against external electric field,

Work done in bringing the charge q₂ against the external electric field and the electric field produced due to charge q₁

Therefore, Total work done = Electrostatic potential energy

Question 81.
A capacitor of unknown connected across a battery of V volt. A charge of 360 pC is stored in it. When the potential across the capacitor is reduced by 120 V, the charge stored in the capacitor becomes 120 pC. Calculate V and the unknown capacitance. What would have been the charge on the capacitor if the voltage were increased by 120 V? (Comptt. Delhi 2015)
Answer:


q₃ = 600 µC would be charge on the capacitor if voltage were incresed by 120 V.

Question 82.
A capacitor of unknown capacitance is connected across a battery of V volt. A charge of 240 pC is stored in it. When the potential across the capacitor is reduced by 80 V, the charge stored in the capacitor becomes 80 pC. Calculate V and the unknown capacitance. What would have been the charge in the capacitor if the voltage were increased by 80 V? (Comptt. Delhi 2015)
Answer:


q₃ = 600 µC would be charge on the capacitor if voltage were incresed by 120 V.
[Answer : V = 120 V, c = 2 μF, Q = 400 μC]

Question 83.
A capacitor of unknown capacitance is connected across a battery of V volt. A charge of 120 μC is stored in it. When the potential across the capacitor is reduced by 40 V, the charge stored in the capacitor becomes 40 μC. Calculate V and the unknown capacitance. What would have been the charge in the capacitor if the voltage were increased by 40 V? (Comptt. Delhi 2015)
Answer:

>
q₃ = 600 µC would be charge on the capacitor if voltage were incresed by 120 V.
[Ans : V = 60 V, c = 2 pF, Q3 = 200 μC].

Question 84.
A parallel plate capacitor of capacitance C is charged to a potential V by a battery. Without disconnecting the battery, the distance between the plates is tripled and a dielectric medium of k = 10 is introduced between the plates is tripled and a dielectric medium of k = 10 is introduced between the plates of the capacitor. Explain giving reasons, how will the following be affected:
(i) capacitance of the capacitor
(ii) charge on the capacitor, and
(iii) energy density of the capacitor. (Comptt. Outside Delhi 2015)
Answer:
Given : d’ = 3d, K = 10, C = ?, Q’ = ?, U’_d= ?
(i) For parallel plate capacitor

Question 85.
Derive the expression for the electric potential at any point P, at distance r from the centre of an electric dipole, making angle a, with its axes. (Comptt. All India 2015)
Answer:
The potential due to the dipole is the sum of potentials due to the charges q and – q

where r₁ and r₂ are the distances of the point P from q and – q, respectively.
Now, by geometry,

If r is much greater than a (r >> a) then,

Using the Binomial theorem and retaining terms upto the first order in air; we obtain,

Electrostatic Potential and Capacitance Class 12 Important Questions Long Answer Type

Question 86.
Derive an expression for the energy stored in a parallel plate capacitor.
On charging a parallel plate capacitor to a potential V, the spacing between the plates is halved, and a dieletric medium of ε_r = 10 is introduced between the plates, without disconnecting the d.c. source. Explain, using suitable expressions, how the
(i) capacitance,
(ii) electric field and
(iii) energy density of the capacitor change. (All India 2008)
Answer:
(a) Consider a parallel plate capacitor with plate area ‘A’ and separation between the plates equal to ‘d’. Suppose at any instant of time charge on the capacitor plate is ‘q’ and potential difference due to this charge is V. To supply a charge ‘dq’ further to the capacitor amount of work required is

Question 87.
(a) Write two properties of equipotential surfaces. Depict equipotential surfaces due to an isolated point charge. Why do the equipotential surfaces get closer as the distance between the equipotential surface and the source charge decreases?
(b) An electric dipole of dipole moment \(\vec{p}\), is placed in a uniform electric field \(\vec{E}\),. Deduce the expression for the torque ‘x acting on it. (Comptt. All India 2008)
Answer:
(a) Properties of equipotential surfaces:
(i) No work is done in moving a test charge over an equipotential surface.
(ii) No two equipotential surfaces can inter-sect each other.
(iii) Equipotential surface due to an isolated point charge is spherical.
(iv) The electric field at every point is normal to the equipotential surface passing through that point. (any two)

For the same charge in the value, V, i.e., when dV = constant,
we have dr \(\propto \frac{1}{\mathrm{E}}\)
Hence, equipotential surface gets closer as the distance between the equipotential surface and the source charge decreases.

Equipotential surface due to an isolated charge
(b) Consider a dipole with charges +q and -q placed in a uniform electric field \(\overrightarrow{\mathrm{E}}\) such that AB = 2a as shown in the figure

Since the dipole experiences no net force in a uniform electric field but experiences a torque (τ) is given by

It tends to rotate the dipole in clockwise direction. To rotate the dipole anti-clock wise has to be done on the dipole.

Question 88.
(a) Obtain the expression for the potential due to an electric dipole of dipole moment p at a point V on the axial line.
(b) Two identical capacitors of plate dimensions l × b and plate separation d have di-electric slabs filled in between the space of the plates as shown in the figure.

Obtain the relation between the dielectric constants K, K₁ and K₂.(Comptt. All India 2013)
Answer:
(a) Potential at a point due to an electric dipole : Let us consider an electric dipole consisting of two equal and opposite charges -q at A and +q at B, separated by a distance 21 with centre at O. We have to calculate potential at a point P, whose polar co-ordinates are (r, 0); i.e. OP = r and ∠BOP = θ, as shown in the figure.
Here AP = r₁, and BP = r₂, we can easily calculate potential as P due to point charges at A and B using V = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r}\).

Total potential at P due to both the charges of the dipole is given by
v = v₁ + v₂

To put this result in a more convenient form, we draw normals from A and B on the line joining O and P. From ∆BOD, we note that OD = l cos θ and from ∆OAC we note that OC = l cos θ. For a small dipole (AB << OP), from the figure, we can take PB = PD and PA = PC.
Hence r₁ = r + l cos θ,
Using these results in equation (1), we get


where we have neglected the term containing second power of l since l << r
In terms of dipole (p = q × 21), we can express this result as

This result shows that unlike the potential due to a point charge, the potential due to a dipole is inversely proportional to the square r of the distance.
Let us now consider its special cases.
Special Cases
Case I : When point P lies on the axial line of the dipole on the side of positive charge,
θ = 0 and cos θ = 1
Then equation (ii) reduces to

Case II : When point P lies on the axial line of the dipole but on the side of negative charge,
θ = 180° and cos θ = 1

Case III :When point P lies on the equatorial line of the dipole (perpendicular bisector of AB), θ = 90° and cos θ = 0
Then V_equitorial = 0 … (i)
Thus, electric potential due to a dipole is zero at every point on the equatorial line of the dipole.

In second case, these two apartments are in parallel, their net capacity would be the sum of two individual capacitances
C₂ = C’₂ + C”₂

Since these are identical capacitors, comparing (i) and (ii),
We have C₁ = C₂

Question 89.
(a) Explain, using suitable diagrams, the difference in the behaviour of a
(i) conductor and
(ii) dielectric in the presence of external electric field. Define the terms polarization of a dielectric and write its relation with susceptibility.
(b) A thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge \(\frac{Q}{2}\) is placed at its centre C and another charge +2Q is placed outside the shell at a distance x from the centre as shown in the figure.

Find
(i) the force on the charge at the centre of shell and at the point A,
(ii) the electric flux through the shell. (Delhi 2015)
Answer:
(a) (i) Behaviour of conductor in an external electric field :

(ii) Behaviour of a dielectric in an external electrical field :

Explanation: In the presence of electric field, the free charge carriers in a conductor move the charge distribution and the conductor readjusts itself so that the net Electric field within the conductor becomes zero.

In a dielectric, the external electric field induces a net dipole moment, by stretching / reorienting the molecules. The electric field, due to this induced dipole moment, opposes, but does not exactly cancel the external electric field.

Polarisation: Induced Dipole moment, per unit volume, is called the polarisation. For Linear isotropic dielectrics having a susceptibility x_c, we have polarisation (p) as:
p = X_cE
(b) (i) Net Force on the charge y, placed at the centre of the shell, is zero.
Force on charge ‘2Q’ kept at point A,

Question 90.
(i) If two similar large plates, each of area A having surface charge densities +a and -a are separated by a distance d in air, find the expressions for
(a) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(b) the potential difference between the plates.
(c) the capacitance of the capacitor so formed.
(ii) Two metallic spheres of radii R and 2R are charged so that both of these have same surface charge density a. If they are connected to each other with a conducting wire, in which direction will the charge flow and why? (All India 2016)
Answer:
(i) Given :


From (i) and (ii), we know that V_2R > V_R
Hence, the bigger sphere will be at a higher potential, so charge will flow from bigger sphere to smaller sphere.

Question 91.
(a) Obtain the expression for the potential due to a point charge.
(b) Use the above expression to show that the potential, due to an electric dipole (length 2a), varies as the ‘inverse square’ of the distance r of the ‘field point’ from the centre of the dipole for r > a. (Comptt. Delhi 2016)
Answer:
(a) Consider a point charge ‘Q’ kept at point O. Let P be the field point at distance r.
At some point p’, the electrostatic force on the unit positive charge is

Question 92.
(a) Define the SI unit of capacitance.
(b) Obtain the expression for the capacitance of a parallel plate capacitor.
(c) Derive the expression for the affective capacitance of a series combination of n capacitors. (Comptt. Delhi 2016)
Answer:
(a) When a charge of one coulomb produces a potential difference of one volt between the plates of capacitor, the capacitance is one farad.

(b)
Capacity of a parallel plate capacitor. A parallel plate capacitor consists of two large plane parallel conducting plates separated by a small distance. We first take the intervening medium between the plates to be vaccum. Let A be the area of each plate and d the separation between them. The two plates have charges Q and – Q. Since d is much smaller than the linear dimension of the plates (d² << A), we can use the result on electric field by an infinite plane sheet of uniform surface charge density. Plate 1 has surface charge density σ = Q/A and Plate 2 has a surface charge density -σ, the electric field in different region is:

In the inner region between the plates 1 and 2, the electric fields due to the two charged plates add up, giving

The capacitance C of the parallel plate capacitor is then

(c) In series combination, charge on each capacitor is same.

Important Questions for Class 12 Physics