Practicing the CBSE Sample Papers for Class 12 Physics with Solutions Set 2 allows you to get rid of exam fear and be confident to appear for the exam.
CBSE Sample Papers for Class 12 Physics Set 2 with Solutions
Time : 3 Hours
Maximum Marks: 70
General Instructions :
- There are 35 questions in all. All questions are compulsory.
- This question paper has five sections: Section A, Section B, Section C, Section D and Section E. All the sections are compulsory.
- Section A contains eighteen MCQs of 1 mark each, Section B contains seven questions of two marks each, Section C contains five questions of three marks each, Section D contains three long questions of five marks each and Section E contains two case study based questions of 4 marks each.
- There is no overall choice. However, an internal choice has been provided in Section B, C, D and E. You have to attempt only one of the choices in such questions,
- Use of calculators is not allowed.
Section – A
The following questions are multiple-choice questions with one correct answer. Each question carries 1 mark. There is no internal choice in this section.
Question 1.
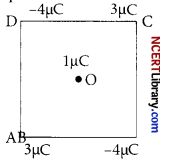
Four point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1 µC placed at the centre of square is: [1]
(a) 7 N
(b) 12 N
(c) 18 N
(d) Zero
Answer:
(d) Zero
Explanation: Forces of repulsion on 1 µC charge at O due to 3 µC charge, at A and C are equal and opposite. So they cancel each other. Similarly, forces of attraction of 1 µC charge at O due to -4 µC charges at B and D are also equal and opposite. So, they also cancel each other.
Hence the net force on the charge of 1 µC at O is zero.
Question 2.
A charge q1 exerts some force on a second charge q2 If third charge q3 is brought near, the force of q1 exerted on q2. [1]
(a) decreases
(b) increases
(c) remains unchanged
(d) increases if q3 is of the same sign as q1 and decreases if q3 is of opposite sign
Answer:
(c) remains unchanged
Explanation: The force will still remain \(\frac{q_1 q_2}{4 \pi \varepsilon_0 r^2}\) according to the superposition principle.
Question 3.
When a current I is set up in a wire of radius r, the drift velocity is vd. If the same current is set up through a wire of radius 2r, the drift velocity will be: [1]
(a) Avd
(b) 2vd
(c) vdd/2
(d) ud /4
Answer:
(d) ud /4
Explanation: As we know that, I = nAevd
or vd ∝ \(\frac{1}{\pi r^2}\)
If r → 2r, then
v’d = \(\frac{1}{\pi(2 r)^2}\)
v’d = \(\frac{v_d}{4}\)
Question 4.
Ampere’s circuital law states that: [1]
(a) the line integral of magnetic field along the boundary of the open surface is equal to po times the total current passing near the surface.
(b) the line integral of magnetic field along the boundary of the open surface is equal to go times the total current passing through the surface.
(c) the surface integral of magnetic field over the open surface is equal to po times the total current passing through the surface.
(d) the surface integral of magnetic field over the open surface is equal to po times the total current passing near the surface.
Answer:
(b) the line integral of magnetic field along the boundary of the open surface is equal to po times the total current passing through the surface.
Explanation: According to Ampere’s circuital law,
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}=\mu_0 \mathrm{I}\)
Question 5.
A coil having N turns, carry a current as shown in the figure. The magnetic field intensity at point P is: [1]

(a) Zero
(b) \(\frac{\mu_0 \mathrm{NI}}{2 \mathrm{R}}\)
(c) \(\frac{\mu_0 \mathrm{NIR}^2}{(\mathrm{R}+x)^2}\)
(d) \(\frac{\mu_0 \mathrm{NIR}^2}{2\left(\mathrm{R}^2+x^2\right)^{3 / 2}}\)
Answer:
(d) \(\frac{\mu_0 \mathrm{NIR}^2}{2\left(\mathrm{R}^2+x^2\right)^{3 / 2}}\)
Explanation: The magnetic field intensity at point P due to current carrying coil having N turns and radius R is given by,
B = \(\frac{\mu_0}{4 \pi} \frac{2 \pi(\mathrm{NI}) \mathrm{R}^2}{\left(\mathrm{R}^2+x^2\right)^{3 / 2}}\)
or = \(\frac{\mu_0 \mathrm{NIR}^2}{2\left(\mathrm{R}^2+x^2\right)^{3 / 2}}\)
Question 6.
The magnetisation of a bar magnet of length 5 cm, cross-sectional area 2 cm² and magnetic moment 1 Am² is : [1]
(a) 2 x 105 A/m
(b) 4 x 105 A/m
(c) 105 A/m
(d) 3 x 105 A/m
Answer:
(c) 105 A/m
Explanation: Given, l = 5 cm = 5 x 10-2 m
A = 2 cm² = 2 x 10-4 m²
and M = 1 Am-2
∴ Magnetisation of bar magnet is given by,
I = \(\frac { M }{ V }\)
= \(\frac { M }{ A × I }\)
= \(\frac{1}{2 \times 10^{-4} \times 5 \times 10^{-2}}=\frac{1}{10^{-5}}\)
= 105 A/m
![]()
Question 7.
For two. coils with number of turns 500 and 200 each of length 1 m and cross-sectional area 4 x 10-4 m², the mutual inductance is: [1]
(a) 0.5 µH
(b) 0.5 H
(c) 5 µH
(d) 0.05 mH
Answer:
(d) 0.05 mH
Explanation: From the formula,

Question 8.
A 40 Ω electric heater is connected to a 200 V, 50 Hz mains supply. The peak value of electric current flowing in the circuit is approximately: [1]
(a) 10 A
(b) 5 A
(c) 7 A
(d) 2.5A
Answer:
(c) 7 A
Explanation:
∵ Irms = \(\frac{E_{\text {rms }}}{R}\)
= \(\frac { 200 }{ 40 }\)
= 5 A
∴ I0 = Irms\(\sqrt{2}\)
= 7.07 A
Question 9.
A linearly polarised electromagnetic wave given as E = E0 \(\hat{i}\) cos (kz – cot) is incident normally on a perfectly reflecting jnfjnj|e wap at z = a. Assuming that the material of the wall is optically inactive, the reflected wave will be given as: [1]
(a) Er = E0\(\hat{i}\)(kz – ωt)
(b) Er = E0\(\hat{i}\)cos(kz + ωt)
(c) Er = – E0\(\hat{i}\)cos(kz + ωt)
(d) Er = E0\(\hat{i}\)sin(kz + ωt)
Answer:
(b) Er = E0\(\hat{i}\)cos(kz + ωt)
Explanation: When a wave is reflected from denser medium, then the type of wave doesn’t change but only its phase changes by 180° or n radian.
Thus, for the reflected wave \(\hat{z}=-\hat{z}, \hat{i}=-\hat{i}\) and additional phase of n in the incident wave.
Given, here the incident electromagnetic wave is,
E = E0\(\hat{i}\)cos(kz – ωt)
The reflected electromagnetic wave is given by
Er = E0(- \(\hat{i}\)) cos[k(-z) – ωt + π]
= -E0\(\hat{i}\) cos [-(kz + ωt) + π]
= E0\(\hat{i}\) cos[-(kz + ωt)]
= E0\(\hat{i}\) cos(kz + ωt)
Question 10.
The refractive index of water is 4/3. Obtain the value of semi-vertical angle of the cone within which the entire outside view would be confined for a fish under water: [1]
(a) 49°
(b) 45°
(c) 32°
(d) 65°
Answer:
(a) 49°
Explanation:
µ = \(\frac{1}{\sin i_c}\)
⇒ sin ic = \(\frac { 1 }{ μ }\) = \(\frac { 3 }{ 4 }\) = 0.75
⇒ ic = \(\frac { θ }{ 2 }\) = sin-1 0.75 = 48.6°
∴ Semi-vertical angle = 48.6°.
Question 11.
The energy levels of a hypothetical one electron atom are shown in the figure. [1]

What is the minimum energy that an electron will have after interacting with this atom in the ground state if the initial kinetic energy of the electrons is 11 eV.
(a) 6eV
(b) 10.3 V
(c) 11 eV
(d) 0.7 eV
Answer:
(d) 0.7 eV
Explanation: Here, E2-E1 = 10-3eV < 11 eV
∴ Electrons can excite the atoms,
Kmin = (11-10.3) = 0.7 eV.
Question 12.
The shortest wavelength in the Balmer series is: [1]
(a) 364.6 nm
(b) 300 nm
(c) 256.8 nm
(d) 200 nm
Answer:
(a) 364.6 nm
Explanation: The shortest wavelength possible for Balmer series is 364.6 nm.
Question 13.
Paschen series of atomic spectrum of hydrogen gas lies in: [1]
(a) Infrared region
(b) Ultraviolet region
(c) Visible region
(d) Partly in ultraviolet and partly in visible region
Answer:
(a) Infrared region
Explanation: Paschen series of atomic spectrum of hydrogen gas lies m infrared region.
As \(\bar{v}=\mathrm{R}\left[\frac{1}{3^2}-\frac{1}{n^2}\right]\)
n = 4,5,6 and so on
![]()
Question 14.
Magnetic flux of 10 μWb is linked with a coil, when a current of 2 mA flows through it. What is the self-inductance of the coil? [1]
(a) 20 mH
(b) 10 mH
(c) 15 mH
(d) 5mH
Answer:
(d) 5 mH
Explanation: We know that,
Φ = LI
L = \(\frac { Φ }{ I }\)
= \(\frac{10 \times 10^{-6}}{2 \times 10^{-3}}\)
= 5 mH
Question 15.
Two charges, each equal to q, are kept at x = – a and x = a on the X-axis. A particle of mass m and charge qo = q/2 is placed at the origin. If charge qo is given a small displacement (y << a) along the Y-axis, the net force acting on the particle is proportional to: [1]
(a) y
(b) \(\frac { 1 }{ y }\)
(c) – y
(d) –\(\frac { 1 }{ y }\)
Answer:
(a) y
Explanation:

(Direction: Question 16 to 18) Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below:
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true and R is not the correct explanation of A.
(c) A is true, but R is false.
(d) A is false, and R is also false.
Question 16.
Assertion: If the temperature of a semiconductor is increased then it’s resistance decreases. [1]
Reason: The energy gap between conduction band and valence band is very small.
Answer:
(a) Both A and R are true and R is the correct explanation of A.
Explanation: In semiconductors, the energy gap between conduction band and valence band is small (≈ 1 e V). Due to temperature rise, electron in the valence band gain thermal energy and may jump across the small energy gap (to the conduction band). Thus, conductivity increases and hence resistance decreases.
Question 17.
Assertion: Phase difference between any two points on a wavefront is 180°. [1]
Reason: It depends on the distance of the two points from the source.
Answer:
(d) A is false, and R is also false.
Explanation: Phase difference between any two points on a wavefront is zero. Also two points on a given wavefront are equidistant from source hence independent of distance.
Question 18.
Assertion : When certain wavelength of light falls on metal surface it ejects electron. [1]
Reason : Light has wave nature.
Answer:
(b) Both A and R are true and R is not the correct explanation of A Explanation: Light is a transverse, electromagnetic wave that can be seen by the typical human. The wave nature of light was first illustrated through experiments on diffraction and interference. Like all electromagnetic waves, light can travel through a vacuum.
Section – B
Question 19.
Name the electromagnetic waves with their frequency range, produced in : [2]
(i) some radioactive decay
(ii) sparks during electric welding
(iii) TV remote
Answer:
(i) Gamma radiations are produced during the radioactive decay of a nucleus. Frequency range is > 3 x 1017 Hz.
(ii) Welding sparks produces ultraviolet rays.
Frequency range is 7.5 x 1014 Hz – 3 x 1016 Hz.
(iii) T.V. remote control uses infrared radiations.
Frequency range is 3 x 1012 Hz – 4.3 x 1014 Hz.
Question 20.
Write the expression, in a vector form, for the Lorentz magnetic force \(\vec{F}\) due to a charge moving with velocity \(\vec{v}\) in a magnetic field \(\vec{B}\). What is the direction of the magnetic force? [2]
Answer:
The Lorentz magnetic force is given by the following relation :
\(\vec{F}\) = q(\(\vec{v}\) x \(\vec{B}\))
Here q, is the magnitude of the moving charge.
The direction of the magnetic force is perpendicular to the plane containing the velocity vector and the magnetic field vector \(\vec{B}\).
Question 21.
Write two important limitations of Rutherford nuclear model of the atom. [2]
OR
Nuclear atomic model is required to explain the results of Rutherford experiment. Why ?
Answer:
Limitations of Rutherford model:
(i) It is not in accordance with the Maxwell’s theory and could not explain the stability of an atom.
(ii) It did not say anything about the arrangement of electrons in an atom.
OR
In Rutherford experiment, a few a-particles are scattered through large angles. Therefore, massive and positive part of atom should be concentrated in a small portion of the atom. The small positive part having almost the entire mass of the atom was called nucleus. Therefore, the main feature of any atom model should require the presence of the central positive and massive nucleus.
Question 22.
You are given two converging lenses of focal lengths 1.25 cm and 5 cm to design a compound microscope. If it is desired to have a magnification of 30, find out the separation between the objective and the eye-piece. [2]
Answer:
Given, fe = 5 cm; f0 = 1.25 cm and M = – 30.
Let L be the tube length (distance between the objective and the eyepiece)
∴ M = \(\frac{-\mathbf{L}}{f_o}\left(1+\frac{\mathrm{D}}{f_e}\right)\)
[D is a constant and equal to the normal distance of clear vision of the human eye]
Hence,
– 30 = – \(\frac{L}{1.25}\left(1+\frac{25}{5}\right)\)
∴ L = \(\frac{30 \times 1.25}{6}\) = 6.25 cm
Hence, the tube length = 6.25 cm.
![]()
Question 23.
Write any two distinguishing features between conductors, semiconductors and insulators on the basis of energy band diagrams. [2]
OR
Explain briefly with the help of necessary diagrams, the forward and the reverse biasing of a p-n junction diode. Also draw their characteristic curves in the two cases.
Answer:
Conductors:
(i) In case of conductors, the valence band is completely filled and the conduction band can have two cases- either it is partially filled with an extremely small energy gap between the valence and conduction bands or it is empty, with the two bands overlapping each other.
(ii) Even when a small current is applied, conductors can conduct electricity.
Insulators:
(i) In case of insulators, the energy gap between the conduction and valence bands is very large and the conduction band is practically empty.
(ii) When an electric field is applied to such kind of material, the electrons find hard to receive such a large amount of energy to reach the conduction band. Thus, the conduction band remains empty. That is why no current flows through insulators.
Semiconductors:
(i) In case of semiconductor, the energy band structure of semiconductors is similar to insulators. But in this case, the size of forbidden energy gap is quite smaller than that of the insulators.
(ii) When an electric field is applied to a semiconductor, the electrons in the valence band find it relatively easier to jump to the conduction band. So, the conductivity of semiconductors lies between the conductivity of conductors and insulators.
OR
Forward biasing: If the positive terminal of the battery is connected to the p-type semiconductor and negative terminal to the n-type semiconductor then it is said to be forward biased.

Characteristics:

Reverse Biasing : If the positive terminal of the battery is connected to the n-type semiconductor and the negative terminal to the p-type semiconductor then it is said to be reverse biased.

Characteristics:

Question 24.
Draw the ray diagram of an astronomical telescope showing image formation in the normal adjustment position. Write the expression for its magnifying power. [2]
Answer:

The magnifying power m is the ratio of the angle P subtended at the eye by the final image to the angle a which the object subtends at the lens or the eye. Hence,
m = \(\frac{\beta}{\alpha}=\frac{h}{f_e} \cdot \frac{f_o}{h}=\frac{f_o}{f_e}\)
Question 25.
Consider two hollow concentric spheres, S1 and S2, enclosing charges 2Q and 4Q respectively as shown in the figure.
(a) Find out the ratio of the electric flux through them.
(b) How will the electric flux through the sphere S1 change if a medium of dielectric constant ‘εr‘ is introduced in the space inside S1 in place of air? [2]

Deduce the necessary expression.
Answer:
(a) Charge enclosed by sphere S1 = 2Q
By Gauss’ law, electric flux through sphere S1 is
Φ1 = \(\frac{2 Q}{\varepsilon_0}\)
Charge enclosed by sphere
S2 = 2Q + 4Q = 6Q
∴ Φ2 = \(\frac{6 \mathrm{Q}}{\varepsilon_0}\)
The ratio of the electric flux is
\(\frac{\phi_1}{\phi_2}=\frac{\frac{2 \mathrm{Q}}{\varepsilon_0}}{\frac{6 \mathrm{Q}}{\varepsilon_0}}=\frac{2}{6}=\frac{1}{3}\)
(b) For sphere S1, the electric flux is
Φ’ = \(\frac{2 Q}{\varepsilon_r}\)
∴ \(\frac{\phi^{\prime}}{\phi_1}=\frac{\varepsilon_0}{\varepsilon_r}\)
⇒ Φ’ = Φ1 x \(\frac{\varepsilon_0}{\varepsilon_r}\)
∵ εr > ε0
∴ Φ’ < Φ1
Therefore, the electric flux through the sphere S2 decreases with the introduction of the dielectric inside it.
Section – C
Question 26.
The magnetic moment vectors μs and μl associated with the intrinsic spin angular momentum S and orbital angular momentum l, respectively, of an electron are predicted by quantum theory (and verified experimentally to a high accuracy) to be given by : [2]
μs = – (e/m) S,
μl = – (e/2m) l
Which of these relations is in accordance with the result expected classically? Outline the derivation of the classical result.
Answer:
\(\overrightarrow{u_1}=-\left(\frac{e}{2 m}\right) \vec{l}\)
It follows from the definition of μ1 and I.
μ1 = iA = (\(\frac { e }{ T }\))πr²
l = mvr = m(\(\frac { 2πr }{ T }\))r
Where, r is the radius of the circular orbit, which the electron of mass m and charge (- e) completes in time T.
Divide (i) by (ii),
\(\frac{\mu_1}{l}=\frac{-e}{\mathrm{~T}} \pi r^2 \times \frac{T}{m \times 2 \pi r^2}=\frac{-e}{2 m}\)
\(\overrightarrow{\mu_1}=-\left(\frac{-e}{2 m}\right) \vec{l}\)
Clearly \(\overrightarrow{\mu_1}\) and \(\vec{l}\) will be antiparallel (both being normal to the plane of the orbit).
In contrast \(\frac{\mu_s}{s}=\frac{e}{m}\). It is obtained on the basis of the quantum mechanics.
Question 27.
In Figure, the magnetic needle has magnetic moment 6.7 x 10-2 A m² and moment of inertia A = 7.5 x 10-6 kg m². It performs 10 complete oscillations in 6.70 s. What is the magnitude of the magnetic field? [2]

Answer:
The time period of oscillation is
T = \(\frac { 6.70 }{ 10 }\) = 0.67 s
Relation between moment of inertia and magnetic field
B = \(\frac{4 \pi^2 \mathrm{I}}{m \mathrm{~T}^2}\)
= \(\frac{4 \times(3.14)^2 \times 7.5 \times 10^{-6}}{6.7 \times 10^{-2} \times(0.67)^2}\)
= 0.01 T
![]()
Question 28.
A rod of length T is moved horizontally with a uniform velocity V in a direction perpendicular to its length through a region in which a uniform magnetic field is acting vertically downward. Derive the expression for the emf induced across the ends of the rod. [2]
OR
Define the term ‘mutual inductance’ between the two coils. Obtain the expression for mutual inductance of a pair of long coaxial solenoids each of length l and radii r1 and r2 (r2 >> r1). Total number of turns in the two solenoids are N1 and N2 respectively.
Answer:
Consider a rod PQ of length l, moving in a magnetic field \(\vec{B}\) with a constant velocity \(\vec{v}\). The length of the rod is perpendicular to the magnetic field and also the velocity is perpendicular to both the rod and field. The free electrons of the rod also move at this velocity \(\vec{v}\) because of which it experiences a magnetic force.

\(\overrightarrow{\mathrm{F}_b}=\overrightarrow{q v} \times \overrightarrow{\mathrm{B}}\)
This force is towards Q to P.
Thus, the free electrons will move towards P and positive charge will appears at Q. An electrostatic field E is developed within the wire from Q to P. This field exerts a force.
\(\overrightarrow{\mathrm{F}_e}=q \overrightarrow{\mathrm{E}}\)
on each free electron, the charge keeps on gathering until
\(\overrightarrow{\mathrm{F}}_b=\overrightarrow{\mathrm{F}}_e\)
⇒ \(|q \vec{v} \times \overrightarrow{\mathrm{B}}|=|q \overrightarrow{\mathrm{E}}|\)
vB = E
After this, resultant force on the free electrons of the wire PQ becomes zero. The potential difference between the ends Q and P is given by,
V = El = vBl
Thus, the potential difference is maintained by the magnetic force on the moving free electron and hence, produces an emf, e = Bvl
OR
Mutual inductance of two coils is equal to the e.m.f. induced in one coil when rate of change of current through the other coil is unity.
Mutual inductance of two coaxial solenoids:
Consider two long co-axial solenoid each of length l with number of turns N1 and N2 wound one over the other. Number of turns per emit length in solenoid, n = \(\frac{\mathrm{N}_1}{\mathrm{l}}\). If I1 is the current flowing in primary solenoid, the magnetic field produced within this solenoid.

The flux linked with each turn of inner solenoid coil is \(\phi_2=B_1 A_2\), where A2 is the cross-sectional area of inner solenoid. The total flux linkage with inner coil of N2 turns.

If n1 is number of turns per unit length of outer solenoid and r2 is radius of inner solenoid, then
M = μon1N2πr2²
Question 29.
(a) Write the important properties of photons which are used to establish Einstein’s photoelectric equation.
(b) Use this equation to explain the concept of (1) threshold frequency and (2) stopping potential. [2]
OR
Write Einstein’s photoelectric equation and mention which important features in photoelectric effect can be explained with the help of this equation.
The maximum kinetic energy of the photoelectrons gets doubled when the wavelength of light incident on the surface changes from to /o. Derive the expressions for the threshold wavelength Ao and work function for the metal surface.
Answer:
(a) The important property of photons that is useful in establishing Einstein’s photoelectric equation is their ability to hold on to the electrons of an atom by their forces of attraction.
(b) Einstein’s photoelectric equation states that.
Emax = hv – Φ
If Emax > 0 then hv – Φ > 0
or hv – hv0 > 0
Here, V0 is the threshold frequency.
When v < v0 there will be no emission of electrons
Hence, v must greater than vo.
Again, loss in KE = gain in electromagnetic PE.
At v = v0 and Emax = eVs = 0.
where, Vs is stopping potential,
or Emax = eVs
where Vs represents the stopping potential.
OR
Einstein’s photoelectric equation is given by
Kmax = \(\frac { 1 }{ 2 }\) mv²max
Kmax = hv – Φ0
or hv = hv0 + \(\frac { 1 }{ 2 }\) mv²max
where Kmax = Maximum kinetic energy of the photoelectron
vmax = Maximum velocity of the emitted photoelectron
m = Mass of the photoelectron
v = Frequency of the light radiation
Φ0 = Work function
h = Planck’s constant
If v0 is the threshold frequency, then the work function can be written as
W = Φ0 = hv0
⇒ Kmax = \(\frac { 1 }{ 2 }\) mv²max = hv0 = h(v – v0)
The above equations explains the following results:
(1) If v < v0, then the maximum kinetic energy is negative, which is impossible. Hence, photoelectric emission does not take place for the incident radiation below the threshold frequency. Thus, the photoelectric emission can take place if v > v0.
(2) The maximum kinetic energy of emitted photoelectrons is directly proportional to the frequency of the incident radiation. This means, that maximum kinetic energy of photoelectron depends only on the frequency of incident light not on the intensity. According to the photoelectric equation,
Kmax = \(\frac { 1 }{ 2 }\) mv²max = hv – Φ0
K1 = \(\frac{h c}{\lambda_1}-\phi_0\)
Let the maximum kinetic energy for the wavelength λ2 be K2.

Work function is the energy required to eject a photoelectron from the metal.
W = \(\frac{h c}{\lambda_0}\)
∴ W = \(\frac{h c\left(2 \lambda_2-\lambda_1\right)}{\lambda_1 \lambda_2}\)
Question 30.
The radius of the innermost electron orbit of a hydrogen atom is 5.3 x 10-11nm. What are the radii of the n-2 and n = 3 orbits? [2]
Answer:
Given: The radius of the innermost orbit of a hydrogen atom,
r1 = 5.3 x 10-11 m.
Consider r2 be the radius of the orbit at n = 2. It is related to the radius of the innermost orbit.
r2 = (n)²r1
= 4 x 5.3 x 10-n-11
= 2.12 x 10-10 m
For n = 3, r3 = (n)² r1
= 9 x 5.3 x 10-11
= 4.77 x 10-10 m
Thus, the radii of an electron for n = 2 and n = 3 orbits are 2.12 x 10-10 m and 4.77 x 10-10 m respectively.
Section – D
Question 31.
(a) Define the term wave front. State Huygen’s principle. [2]
Consider a plane wave front incident on a thin convex lens. Draw a proper diagram to show how the incident wave front traverses through the lens and after refraction focusses on the focal point of the lens, giving the shape of the emergent wave front.
(b) Explain the following, giving reasons:
(i) When monochromatic light is incident on a surface separating two media, the reflected and refracted light both have the same frequency as the incident frequency.
(ii) When light travels from a rarer to a denser medium, the speed decreases. Does this decrease in speed imply a reduction in the energy carried by the wave?
(iii) In the wave picture of light, intensity of light is determined by the square of the amplitude of the wave. What determines the intensity in the photon picture of light?
OR
(a) Use Huygen’s principle to show how a plane wavefront propagates from a denser to rarer medium. Hence verify Snell’s law of refraction.
(b) Define the term, “refractive index” of a medium. Verify Snell’s law of refraction when a plane wavefront is propagating from a denser to a rarer medium.
Answer:
(a) Wave front: A wave front is the locus of all the points in space that reach a particular distance by a propagating wave in same phase at any instant.
Huygen’s principle: It is based on two assumptions:
(i) Each point of the wavefront behaves like a source of secondary disturbances and secondary wavelets from there points spread out in all directions with the same speed as that of the original wave front.
(ii) When we draw an envelope in the forward direction of the secondary disturbances at any instant, And this envelope tells the new position of the wavefront at that instant.

(b) (i) Both the reflection and refraction takes place due to the interaction of light with the atoms at the
surface of the separation. Light incident on these atoms, force them to vibrate with the frequency of light. But, the light emitted by these charged atoms is equal to their own frequency of oscillation. So, both the reflected and refracted lights have same frequency No, Hence, frequency remains changed.
(ii) For a given frequency the energy carried by a wave depends on the amplitude of the wave. It does not depend on the speed of the wave propagation. Hence the energy of the wave remains same and does not decrease.
(iii) The intensity of light is determined by the number of photons incident per unit area around the point at which intensity is to be determined.
OR
(a) In ∆ ABC,

It is Snell’s law.
(b) The refractive index of a medium is defined as the ratio of speed of light in vacuum to that of the speed of the light in medium.
i.e., n = \(\frac { c }{ v }\)
Where, n = refractive index of medium when light ray passes from vacuum into a medium.
C = velocity of light in vacuum
v = velocity of light in the medium
Proof of Snell’s law of refraction:

When a wavefront travels from one medium to other, it deviates from its path. In travelling from one medium to other, the frequency of wave remains same and speed and wavelength changes. Let, XY be a surface separating two media ‘1’ and ‘2’. Let the speed of waves of v1 and v2.
Suppose, a plane wavefront AB in first medium is incident obliquely on the boundary surface XY and its end touches the surface at A at time t = 0, while the other end B reaches the surface at point B’ after time-interval’?
Clearly, BB’ = v1t.
In the same time, wavelets starts from A and reaches A’ in time ‘t’ with velocity v2.
Therefore, AA’ = v21
According to Huygen’s principle, A’B’ is the new position of the wavefront in second medium. A’B’ is a refracted wavefront.
Let, the incident wavefront (AB) and refracted wavefront (A’B’) makes angle i and r with surface XY.
In ∆AB’B,
∠ABB’ = 90° BB’
∴ sin i = \(\frac{\mathrm{BB}^{\prime}}{\mathrm{AB}^{\prime}}=\frac{v_1 t}{\mathrm{AB}^{\prime}}\) … (i)
In ∆AA’B’,
∠AA’B’ = 90°
∴ sin r = \(\frac{\mathrm{AA}^{\prime}}{\mathrm{AB}^{\prime}}=\frac{v_2 t}{\mathrm{AB}^{\prime}}\) … (ii)
Dividing equation (i) by (ii), we get
\(\frac{\sin i}{\sin r}=\frac{v_1}{v_2}\) = constant
Hence, ratio of sine of angle of incidence and the sine of angle of refraction for a given pair of media is constant. This is Snell’s law of refraction.
![]()
Question 32.
(a) (i) Define the term drift velocity. [2]
(ii) On the basis of electron drift, derive an expression for resistivity of a conductor in terms of number density of free electrons and relaxation time. On what factors does resistivity of a conductor depend?
(b) A resistance of R draws current from a potentiometer. The potentiometer wire, AB, has a total resistance of R0. A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of potentiometer wire.

OR
(a) (i) Define the term ‘conductivity’ of a metallic wire. Write its SI unit.
(ii) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E.
(b) Find the relation between drift velocity and relaxation time of charge carriers in a conductor. A conductor of length L is connected to a d.c. source of emf ‘E’. If the length of the conductor is tripled by stretching it, keeping ‘E’ constant, explain how its drift velocity would be affected.
Answer:
(a) (i) Drift velocity is defined as the average velocity with which the free electrons are drifted towards the positive terminal under the effect of applied electric field. Thermal velocities are randomly distributed and average thermal velocity is zero.

(ii) We know that the current flowing through the conductor is

Where R = \(\frac{m l}{n \mathrm{~A} e^2 \tau}\) is a constant for a particular conductor at a particular temperature and is called the resistance of the conductor.
R = \(\left(\frac{m}{n e^2 \tau}\right) \frac{l}{\mathrm{~A}}=\frac{\rho l}{\mathrm{~A}}\)
ρ = \(\left(\frac{m}{n e^2 \tau}\right)\)
Where, ρ is the specific resistance or resistivity of the material of the wire. It depends on number of free electron per unit volume and temperature.
(b) The equivalent resistance between A and C,

OR
(a) (i) Conductivity of a metallic wire is defined as its ability to allow electric charges or heat to pass through it.
Numerically, conductivity is reciprocal of resistivity.
SI unit: ohm-1 m-1 or mho m-1 or Sm-1.
(ii) Consider a potential difference V be applied across a conductor of length l and cross-section A. Electric field inside the conductor,
E = \(\frac { V }{ l }\)
Due to the external field the free electrons inside the conductor drift with velocity vd.
Let, number of electrons per unit volume = n, charge on an electron = e
∴ Total electrons in length l = nAl
and Total charge q = neAl
Time taken by electrons to enter and leave the conductor.

Relation between current density and field :
For an electron, charge q = – e.
and current density, J = \(\frac { I }{ A }\) = – nevd [from (i)]
J = (-ne)\(\left(\frac{-e \mathrm{E} \tau}{m}\right)=\left(\frac{n e^2 \tau}{m}\right)\)E
⇒ J = σE [from (ii)]
which is the required relation.
(b) All free electrons suffer collisions with the heavy fixed ions inside the conductor. After collisions, these electrons again moves with the same speed, but in random directions. So, at given time, net velocity of the electrons is zero i.e.,
\(\overrightarrow{u_{a v g}}=\frac{\overrightarrow{u_1}+\overrightarrow{u_2}+\ldots \ldots+\overrightarrow{u_n}}{n}\) = 0
If the electric field established inside the conductor, electrons get accelerated, so
a = – \(\frac { eE }{ m }\)
Now, the average velocity of all electrons is given by
\(\overrightarrow{u_d}=\overrightarrow{u_{a v g}}-\frac{\varepsilon \mathrm{E}}{m} \tau\)
\(\overrightarrow{u_d}=0-\frac{\varepsilon \mathrm{E}}{m} \tau\)
where τ is the average relaxation time.
But E = \(\frac { V }{ l }\)
\(\overrightarrow{u_d}=-\frac{\varepsilon \mathrm{V} \tau}{m l}\)
ud ∝ \(\frac { 1 }{ l }\)
As the drift velocity is inversely proportional to its length, so the drift velocity would be reduced by one- third if the length of the conductor is tripled.
Question 33.
(a) A slab of material of dielectric constant k has same area as that of the plates of parallel plate capacitor but has the thickness d/2, where d is the separation between the plates. Derive expression for its capacitance when the slab is inserted between the plates of the capacitor. [2]
(b) A capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 360 μC. When potential across the capacitor is reduced by 120 V, the charge stored in it becomes 120 μC.
Calculate:
(i) The potential V and unknown capacitance C.
(ii) What will be the charge stored in the capacitor, if the voltage applied had increased by 120 V?
OR
(a) A parallel plate capacitor of capacitance C is charged to a potential V. It is then connected to another uncharged capacitor having the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
(b) Two capacitors of unknown capacitances C1 and C2 are connected first in series and then in parallel across a battery of 100 V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively, determine the value of C1 and C2. Also calculate the charge on each capacitor in parallel combination.
Answer:
(a) Initially when there is vacuum between the two plates, the capacitance of the two parallel plates is
C = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\)
Here, A is area of plates and d is separation between the plates.
Let capacitor is connected with battery. Thus electric field inside the capacitor will be produced and it is given by E.
As soon as dielectric slab of thickness t = \(\frac { d }{ 2 }\) inserted the electric field inside slab (f) will be Eo and will be Eo, (Eo = kE).
Now potential difference between the plates will be as follows :

(b) (i) Initial voltage, V1 = V volts and charge stored
Q1 = 360μC
Q1 = CV1
Changed potential,
V2 = V – 120
Q2 = 120 μC
Q2 = cv2
By applying (i) divided by (ii), we get
\(\frac{\mathrm{Q}_1}{\mathrm{Q}_2}=\frac{\mathrm{CV}_1}{C \mathrm{~V}_2}\)
⇒ \(\frac{360}{120}=\frac{V}{V-120}\)
⇒ V = 180 V
Hence, C = \(\frac{\mathrm{Q}_1}{\mathrm{~V}_1}=\frac{360 \times 10^{-6}}{180}\)
= 2 x 10-6 F
= 2 μF
(ii) If the voltage applied had increased by 120 V, then
V3 = 180 +120 = 300 V
Hence charge stored in capacitor,
Q3 = CV3
= 2 x 10-6 x 300 = 600 μC
OR
(a) Let ‘q’ be the charge on the charged capacitor.
Energy stored in it is,
U = \(\frac{q^2}{2 C}\)
When another similar uncharged capacitor is connected, the net capacitance of the system is,
C’ = 2C
The charge on the system is constant. So, the energy stored in the system now is,

(b) When the capacitors are connected in parallel.
Equivalent capacitance, Cp = C1 + C2
The energy stored in the combination of the capacitors,
Ep = \(\frac { 1 }{ 2 }\)Cp V²
⇒ Ep = \(\frac { 1 }{ 2 }\)(C1 + C2) (100)² = 0.25 J
⇒ (C1+C2) = 5 x 10-5
When the capacitors are connected in series.
Equivalent capacitance,
\(C_s=\frac{C_1 C_2}{C_1+C_2}\)
The energy stored in the combination of the capacitors,

Solving (i) and (ii), we get
C1 = 38.2 μF and C2 = 11.8 pF
When the capacitors are connected in parallel, the charge on each of them can be obtained as follows :
Q1 = C1V = 38.2 x 10-6 x 100
= 38.2 x 10-4 4 C
Q2 = C2V = 11.8 x 10-6 x 10-4
= 11.8 x 10-4 C
Section – E
Question 34.
Case Study: Optical fiber
Read the following paragraph and answer the questions. [4]
Optical fiber is made up of good quality fiber of glass, quartz etc. The diameter of the fiber is of the order of 10-2 m and refractive index of the material is of the order of 1.5. The refractive index of outer layer of these fibers is slightly less than 1.5.
When light fall on one end of optical fiber then due to total internal reflection, whole light comes out from the other end.

(i) When light enters in optical fiber, how much light comes out from other end?
(ii) Which material is used in making optical fibers.
(iii) Write the principle on which of optical fibers work.
OR
(iii) What should be the refractive index of outer material of optical fiber if internal material has refractive index 1.49?
Answer:
(i) There is no dissipation of light intensity, therefore 100% light comes out from other end.
(ii) Quartz is used in making optical fibre.
(iii) Optical fibre is based on the principle of total internal reflection, according to that when a light travels from a denser medium to a rarer medium, it comes back to same medium for a certain value of angle of incidence.
OR
(iii) Refractive index of outer material must be less than that of inner material as light entering from denser medium to rarer medium i.e., < 1.49.
![]()
Question 35.
Case Study: p-n junction diode
Read the following paragraph and answer the questions. [4]
The potential barrier in the p-n junction diode is the barrier in which the charge requires additional force for crossing the region. In other words, the barrier in which the charge carrier stopped by the obstructive force is known as the potential barrier.
When a p-type semiconductor is brought into a close wtih rc-type semiconductor, we get a p-n junction with a barrier potential 0.4 V and width of depletion region is 4.0 x 10-7 m. This p-n junction is forward biased with a battery of voltage 3V and negligible internal resistance, in series with a resistor of resistance R, ideal millimeter and key K as shown in figure. When key is pressed, a current of 30 mA passes through the diode.

(iii) When the voltage will be the same that of the potential barrier disappears resulting in flow of current.
OR
(i) Calculate the intensity of the electric field in the depletion region for which p-n junction is unbiased.
(ii) Find the resistance of resistor R.
(iii) If the voltage of the potential barrier is Vo. A voltage V is applied to the input, at what moment will the barrier disappear?
OR
(iii) If an electron with speed 4.0 x 105 ms-1 approaches the p-n junction from the n-side, find the speed with which it will enter the p-side.
Answer:
(i) E = \(\frac{V_B}{d}=\frac{0.4}{4.0 \times 10^{-7}}\) = 1.0 x 106 Vm-1
(ii) Potential difference across, R = 3 – 0.4 = 2.6 V
Resistance, R = \(\frac{\text { Potential difference }}{\text { Current }}\)
= \(\frac{2.6}{20 \times 10^{-3}}\)
= 130 Ω
(iii) When the voltage will be the same that of the potential barrier disappears resulting in flow of current.
OR
(iii) \(\frac { 1 }{ 2 }\)mv1² = eVB + \(\frac { 1 }{ 2 }\)mv2²
⇒ \(\frac { 1 }{ 2 }\) x (9.1 x 10-31) x (4 x 105)² = 1.6 x 10-9 x (0.4) + \(\frac { 1 }{ 2 }\) x 9.1 x 10-31 x v2²
on solving, we get
v2 = 1.39 x 105 ms-1