CBSE Sample Papers for Class 12 Maths Set 1 with Solutions

Practicing the CBSE Sample Papers for Class 12 Maths with Solutions Set 1 allows you to get rid of exam fear and be confident to appear for the exam.

CBSE Sample Papers for Class 12 Maths Set 1 with Solutions

Time : 3 Hours
Maximum Marks: 80

General Instructions :

1. This question paper contains five sections – A. B. C. D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section – A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section – B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
4. Section – C has 6 Short Answer (SA)-type questions of 3 marks each.
5. Section – D has 4 Long Answer (LA)-type questions of 5 marks each.
6. Section – E has 3 source based/case based/passage based/integrated units of assessment (4 marks each) with sub parts.

Section – A
(Multiple Choice Questions)
Each question carries 1 mark

Question 1.
If A = [a_ij] is a skew-symmetric matrix of order n, then
(a) a_ij = \(\frac{1}{a_{j i}}\) ∀i, j
(b) a_ij 0 ∀i, j
(c) a_ij = 0 where i = j
(d) a_ij = 0 where i = j
Solution:
(c) a_ij = 0 where i = j

Explanation: Given skew-symmetric matrix A=[a_ij]
The (i, j)^th element will always negative of (j, i)^th element Hence, the (i, j)^th element will be zero.

Question 2.
If A is a square matrix of order 3, |A’| = – 3, then |AA’| =
(a) 9
(b) -9
(c) 3
(d) -3
Solution:
(a) 9

Explanation: We have given |A’| = – 3
By, the property det A = det A’
So, |A| = – 3
|AA’| = |A| |A’| = -3 x (-3) = 9

Question 3.
The area of a triangle with vertices A, B, C is given by:
(a) \(|\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}|\)
(b) \(\frac { 1 }{ 2 }\)\(|\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}|\)
(c) \(\frac { 1 }{ 4 }\)\(|\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}|\)
(d) \(\frac { 1 }{ 8 }\)\(|\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}|\)

Solution:
(b) \(\frac { 1 }{ 2 }\)\(|\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}|\)
Explanation: As we know area of parallelogram with adjacent sides AB and AC = \(|\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}|\)
So, the area of the triangle with vertices A, B, C = \(\frac { 1 }{ 2 }\)\(|\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}|\)

Question 4.
The value of ‘k’ for which the function

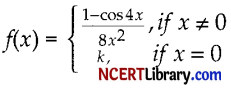
is continuous at x = 0 is:
(a) 0
(b) – 1
(c) 1
(d) 2
Solution:
(c) 1

Explanation: The functionf is continuous at x = 0 if
= f(0)
We have f(0) = k and

Hence k = 1

Question 5.
If f(x) = x + \(\frac { 1 }{ x }\), then f(x) is
(a) x² + log |x| + C
(c) \(\frac { x }{ 2 }\) + log |x| + C
(b) \(\frac{x^2}{2}\) + log | x | + C
(d) \(\frac { x }{ 2 }\) – log | x | + C
Solution
(d) \(\frac { x }{ 2 }\) – log | x | + C

Explanation: By integration
∫f ‘(x) dx = ∫(x + \(\frac { 1 }{ x }\) )dx
∫f ‘(x) = ∫(x + \(\frac { 1 }{ x }\) )dx
\(\frac{x^2}{2}\) + log |x| + C

Question 6.
If m and n, respectively, are the order and the degree of the differential equation \(\frac { d }{ dx }\) [(\(\frac { dy }{ dx }\))]⁴ = 0, then
m + n =
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(c) 3
Explanation: Given differential equation is \(\frac { d }{ dx }\) [(\(\frac { dy }{ dx }\))]⁴ = 0

By chain rule, we get 4 (\(\frac { d }{ dx }\))³ \(\frac{d^2 y}{d x^2}\) = 0
m = 2, n = 1
sum = 2 + 1 = 3

Question 7.
The solution set of the inequality 3x + 5y < 4 is:
(a) an open half-plane not containing the origin.
(b) an open half-plane containing the origin.
(c) the whole XY-plane not containing the line 3x + 5y = 4.
(d) a closed half plane containing the origin.
Solution:
(b) an open half-plane containing the origin.

Explanation: The strict inequality represents an open half plane and it contains the origin as (0, 0) satisfies it.

Question 8.
The scalar projection of the vector 3\(\hat{i} \) – \(\hat{j} \) – 2\(\hat{k} \) on the vector \(\hat{i} \) + 2\(\hat{j} \) – 3\(\hat{k} \) is:
(a) \(\frac{7}{\sqrt{14}}\)
(b) \(\frac { 7 }{ 14 }\)
(c) \(\frac { 6 }{ 13 }\)
(d) \(\frac { 7 }{ 2 }\)
Solution:
(a) \(\frac{7}{\sqrt{14}}\)
Explanation: Projection of \(\vec{a}\) on \(\vec{b}\) is

Question 9.
The value of
is
(a) log 4
(b) log \(\frac { 3 }{ 2 }\)
(c) \(\frac { 1 }{ 2 }\) log 2
(d) log \(\frac { 9 }{ 4 }\)
Solution:
(c) \(\frac { 1 }{ 2 }\) log 2

Explanation: let

Question 10.
If A, B are non-singular square matrices of the same order, then (AB^-1)^-1 =
(a) A^-1 B
(b) A^-1 B^-1
(c) BA^-1
(d) AB
Solution:
(c) BA^-1

Explanation: By the property, if A and B are two invertible matrices of the same order then AB is also invertible and moreover
(AB)^-1 = B^-1 A^-1
Thus, (AB^-1 )^-1 = (B^-1)^-1 A^-1 = BA^-1
[ (P^-1)^-1 = P]

Question 11.
The comer points of the shaded unbounded feasible region of an LPP are (0, 4), (0.6, 1.6) and (3, 0) as shown in the figure. The minimum value of the objective function Z = 4x + 6y occurs at

(a) (0.6, 1.6) only
(b) (3, 0) only
(c) (0.6, 1.6) and (3, 0) only
(d) at every point of the line-segment joining the points (0.6, 1.6) and (3, 0)
Solution:
(d) at every point of the line-segment joining the points (0.6, 1.6) and (3, 0)

Explanation: The minimum value of the objective function occurs at two adjacent comer points (0.6,1.6) and (3,0) and there is no point in the half plane 4x + 6y <12 is common with the feasible region. So, the minimum value occurs at every point of the line-segment joining the two points.

Question 12.
If
,then the possible value(s) of ‘x’ is/are:
(a) 3
(b) \(\sqrt{3}\)
(c) – \(\sqrt{3}\)
(d) \(\sqrt{3}\), – \(\sqrt{3}\)
Solution
(d) \(\sqrt{3}\), – \(\sqrt{3}\)

Explanation: We have to find determinant

Put both equations equal
– 18 = 2x² – 24
2x² = 6
x² = 3
x = ± \(\sqrt{3}\)

Question 13.
If A is a square matrix of order 3 and |A| = 5, then | ad j A | =
(a) 5
(b) 25
(c) 125
(d) \(\frac { 1 }{ 5 }\)
Solution:
(b) 25

Question 14.
Given two independent events A and B such that P(A) = 0.3, P(B) = 0.6 and P(A’ ∩ B’) is:
(a) 0.9
(b) 0.18
(c) 0.28
(d) 0.1
Solution:
(c) 0.28

Explanation: As A and B are independent, A’ and B’ are also independent.
P(A’) = 1 – P(A) = 1 – 0.3 = 0.7
P(B’) = 1 – P(B) = 1 – 0.6 = O.4
P(A’∩B’) = P(A’) x P(B’)
= 0.7 x 0.4
= 0.28

Question 15.
The general solution of the differential equation ydx – xdy = O is:
(a) xy = C
(b) x = Cy²
(c) y = Cx
(d) y = Cx²
Solution:
(c) y = Cx

Explanation: We have given differential equation is
ydx – xdy = 0
\(\frac { dy }{ y }\) = \(\frac { dx }{ x }\)
Taking integration both sides
∫\(\frac { dy }{ y }\) = ∫\(\frac { dx }{ x }\) + log C
logy = Iogx + logC
y = Cx

Question 16.
If y = sin^-1 x, then (1 – x²) y₂ is equal to:
(a) xy₁
(c) xy₂
(b) xy
(d) x²
Solution:
(a) xy₁

We have given y = sin^-1 x
Explanation: dy 1 (Differentiating given y w.r.t. x)
Y₁ = \(\frac { dy }{ dx }\) = \(\frac{1}{\sqrt{1-x^2}}\)
Again, differentiating
y₂ = \(=\frac{d^2 y}{d x^2}\) = \(\frac { d }{ dx }\) \(\frac{1}{\sqrt{1-x^2}}\)
y₂ = x. (1 – x²)^-3/2
Now put in (1 – x²)y₂
(1 – x²).x. (1 – x²)^-3/2 = (1 – x²)^-1/2 x
= \(\frac{1}{\sqrt{1-x^2}}\) [y₁ = \(\frac{1}{\sqrt{1-x^2}}\)]
= x. y₁

Question 17.
If two vectors \(\vec{a}\) and \(\vec{b}\) are such that |\(\vec{a}\)| = 2, |\(\vec{b}\)| = 3 and \(\vec{a}\) . \(\vec{b}\) =4, then |\(\vec{a}\) – 2\(\vec{b}\)| is equal to:
(a) \(\sqrt{2}\)
(b) 2\(\sqrt{6}\)
(c) 24
(d) 2\(\sqrt{2}\)
Solution:
(b) 2\(\sqrt{6}\)

Explanation: Firstly, we will square of |\(\vec{a}\) – 2\(\vec{b}\)|
So, |\(\vec{a}\) – 2\(\vec{b}\)|² = (\(\vec{a}\) – 2\(\vec{b}\)) . (\(\vec{a}\) – 2\(\vec{b}\))
= \(\vec{a}\) . \(\vec{a}\) – 4\(\vec{a}\) . \(\vec{b}\) + 4 \(\vec{b}\) .
\(\vec{b}\)
= |\(\vec{a}\)|² – 4 \(\vec{a}\) . \(\vec{b}\) + 4 \(\vec{b}\) . \(\vec{b}\)
= |\(\vec{a}\)|² – 4 \(\vec{a}\) . \(\vec{b}\) + 4 |\(\vec{b}\)|²
Put the value of |\(\vec{a}\)|, |\(\vec{b}\)| and \(\vec{a}\) . \(\vec{b}\)
= 4 – 16 + 36 = 24
|\(\vec{a}\) – 2 \(\vec{b}\)|² = 24
|\(\vec{a}\) – 2 \(\vec{b}\)| = 2\(\sqrt{6}\)

Question 18.
P is a point on the line joining the points A(0, 5, – 2) and B(3, – 1, 2). If the x-coordinate of P is 6, then its z – coordinate is:
(a) 10
(b) 6
(c) – 6
(d) – 1o
Solution:
(b) 6
Explanation: The line through the points (0, 5, – 2) and (3, – 1, 2) is
\(\frac { x }{ 3 – 0 }\) = \(\frac { y – 5 }{ – 1 – 5 }\) = \(\frac { z + 2 }{ 2 + 2 }\)
\(\frac { x }{ 3 }\) = \(\frac { y – 5 }{ – 6 }\) = \(\frac { z + 2 }{ 4 }\) = k
∵ P be a point on line
∴ P = (3k, – 6k + 5, 4k – 2)
3k = 6
k = 2 (∵ x – coordinate is 6)
∴ z – coordinate = 4k – 2 = 6
Assertion – Reason Based Question

Question 19.
Assertion (A): The domain of the function sec^-1 2x is ( – ∞, – \(\frac { 1 }{ 2 }\) ] ∪[\(\frac { 1 }{ 2 }\), ∞)
Reason (R): sec^-1 (- 2) = – \(\frac { π }{ 4 }\)
Solution
(c) A is true but R is false.

Explanation: sec^-1 x is defined if x ≤ – 1 or x ≥ 1. Hence, sec^-1 2x will be defined if x ≤ – \(\frac { 1 }{ 2 }\) or x ≥ \(\frac { 1 }{ 2 }\)
Hence, A is true
The range of the function sec^-1 x is [0, π] – {\(\frac { π }{ 2 }\)}
R is false

Question 20.
Assertion (A): The acute angle between the line \(\bar{r}\) = \(\hat{i}\) + \(\hat{j}\) + 2\(\hat{k}\) + λ(\(\hat{i}\) – \(\hat{j}\)) and the x-axis is \(\frac { π }{ 4 }\).
Reason (R): The acute angle between the lines
\(\bar{r}\) = x₂ \(\hat{i}\) + y₁\(\hat{j}\) + z₁\(\hat{k}\) + λ(a₁\(\hat{i}\) + b₁\(\hat{j}\) + c₁\(\hat{k}\)) and
\(\bar{r}\) = x₂ \(\hat{i}\) + y₂\(\hat{j}\) + z₂\(\hat{k}\) + μ(a₂\(\hat{i}\) + b₂\(\hat{j}\) + c₂\(\hat{k}\)) is given by cos θ = \(\frac{\left|a_1 a_2+b_1 b_2+c_1 c_2\right|}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a_2^2+b_2^2+c_2^2}}\)
Solution:
(a) Both A and R are true and R is the correct explanation of A.
Explanation: The equation of the x-axis may be written as \(\vec{r}\) = k\(\hat{i}\) . Hence the acute angle θ between the given line and the x-axis is given by
Cos θ = \(\frac{|1 \times 1+(-1) \times 0+0 \times 0|}{\sqrt{1^2+(-1)^2+0^2} \times \sqrt{1^2+0^2+0^2}}\) = \(\frac{1}{\sqrt{2}}\)
Cos θ = \(\frac{1}{\sqrt{2}}\)
θ = Cos^-1 \(\frac{1}{\sqrt{2}}\)
θ = \(\frac{π}{\sqrt{4}}\)

Section – B
This section comprises of very short answer type-questions (VSA) of 2 marks each

Question 21.
Find the value of sin^-1 [ Sin (\(\frac { 13π }{ 7 }\))]
OR
Prove that the functionf is surjective, where f : N —> N such that

Is the function injective? Justify your answer.
Solution:
We have given sin^-1 [ Sin (\(\frac { 13π }{ 7 }\))]
We can write
\(\frac { 13π }{ 7 }\) = 2π – \(\frac { π }{ 7 }\)
∴sin^-1 [ Sin (2π – \(\frac { π }{ 7 }\))
= sin^-1 [ Sin (- \(\frac { π }{ 7 }\)) [ Since, sin (2π – θ) = sin (-θ)]
= – \(\frac { π }{ 7 }\) [sin^-1 will cancel by sin]

OR

We have given function

Let y ∈ N (codomain).
Then there exist 2y ∈ N (domain) such that
f (2y) = \(\frac { 2y }{ 2 }\) = y. Hence f is surjective
1,2 ∈ N (domain) such that
f(1) = 1 = f(2)
So, there is one image of two domains of a function.
Hence,f is not injective or one-one function.

Question 22.
A man 1.6 m tall walks at the rate of 0.3 m/sec away from a street light that is 4 m above the ground. At what rate is the tip of his shadow moving? At what rate is his shadow lengthening?
Solution:
Let AB represent the height of the street light from the ground. At any time t seconds, let the man represented as ED of height 1.6 m be at a distance of x m from AB and the length of his shadow EC be y m.
Using similarity of triangles, we have
\(\frac { 4 }{ 1.6 }\) = \(\frac { x + y }{ y }\)
= 3 y = 2x
Differentiating both sides w.r.t. t, we get
\(\frac { x + y }{ y }\) = \(\frac { 2dx }{ dt }\)
\(\frac { dy }{ dt }\) = \(\frac { 2 }{ 3 }\) x 0.3 = 0.2

At any time t seconds, the tip of his shadow is at a distance of (x + y) m from AB.
The rate at which the Up of his shadow moving = (\(\frac { dx }{ dt }\) + \(\frac { dy }{ dt }\)) = 0.5 m/s
The rate at which his shadow is lengthening = \(\frac { dy }{ dt }\) m/s = 0.2 m/s

Question 23.
If \(\vec{a}\) = \(\hat{i}\) – \(\hat{j}\) + 7 \(\hat{k}\) and \(\vec{b}\) = 5\(\hat{i}\) – \(\hat{j}\) + λ \(\hat{k}\) then find the value of X so that the vectors \(\vec{a}\) + \(\vec{b}\) and \(\vec{a}\) – \(\vec{b}\) are orthogonal.

OR

Find the direction ratios and direction cosines of a line parallel to the line whose equations are 6x – 12 = 3y + 9 = 2z – 2.
Solution:
We have given two vectors
\(\vec{a}\) = \(\hat{i}\) – \(\hat{j}\) + 7 \(\hat{k}\) and \(\vec{b}\) = 5\(\hat{i}\) – \(\hat{j}\) + λ \(\hat{k}\)
The condition for which two vectors will be orthogonal is
(\(\vec{a}\) + \(\vec{b}\)) . (\(\vec{a}\) – \(\vec{b}\)) = 0
\(\vec{a}\) + \(\vec{b}\) = 6\(\hat{i}\) – 2\(\hat{j}\) + (7 + λ )\(\hat{k}\)
\(\vec{a}\) – \(\vec{b}\) = -4\(\hat{i}\) + (7 + λ )\(\hat{k}\)
(\(\vec{a}\) + \(\vec{b}\)) . (\(\vec{a}\) – \(\vec{b}\)) = – 24 + (49 – λ²) = 0
25 – λ² = 0
λ² = 25
λ = ± 5

OR

The equation of the line are 6x – 12 = 3y + 9 = 2z – 2, which can be written in standard symmetric form
\(\frac { x – 2 }{ 1/6 }\) = \(\frac { y – (-3) }{ 1/3 }\) = \(\frac { z – 1 }{ 1/2 }\)
Since, lines are parallel, we have \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
Hence, the required direction ratios are
(\(\frac { 1 }{ 6 }\),\(\frac { 1 }{ 3 }\),\(\frac { 1 }{ 2 }\) ) or (1,2,3)
The direction ratios of a line parallel to this line are (1, 2, 3) and \(\sqrt{(1)^2+(2)^2+(3)^2}\) =
\(\sqrt{4}\)
The required direction cosines are (\(\frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}}\))

Question 24.
If y \(\sqrt{1-x^2}\) + x \(\sqrt{1-y^2}\) =1, then prove that \(\frac { dy }{ dx }\) = – \(\sqrt{\frac{1-y^2}{1-x^2}}\)
Solution:
We have y \(\sqrt{1-x^2}\) + x \(\sqrt{1-y^2}\) =1,
Sin^-1 x = A and Sin^-1 y = B.
The x = sin A and y = sin B
y \(\sqrt{1-x^2}\) + x \(\sqrt{1-y^2}\) =1,
Sin B \(\sqrt{1-\sin ^2 A}\) + sin A \(\sqrt{1-\sin ^2 B}\) = 1
sin B cos A + Sin A cos B = 1
sin (A + B) = 1
A + B = sin^-1 1 = \(\frac { π }{ 2 }\)
sin^-1 x + sin^-1 y = \(\frac { π }{ 2 }\)
Differentiate w.r.t.x, we get
\(\frac { d }{ dx }\)(sin^-1 x ) + \(\frac { d }{ dx }\)(sin^-1 y ) = \(\frac { d }{ dx }\) (\(\frac { π }{ 2 }\))
\(\frac{1}{\sqrt{1-x^2}}\) + \(\frac{1}{\sqrt{1-y^2}}\) \(\frac { dy }{ dx }\) = 0
\(\frac{1}{\sqrt{1-y^2}}\) \(\frac { dy }{ dx }\) = \(\frac{1}{\sqrt{1-x^2}}\)
\(\frac { dy }{ dx }\) = – \(\sqrt{\frac{1-y^2}{1-x^2}}\)

Question 25.
Find |\(\vec{x}\)| if (\(\vec{x}\) – \(\vec{a}\) ) . (\(\vec{x}\) + \(\vec{a}\)) = 12, where a is a unit vector.
Solution:
As we have given \(\vec{a}\) is an unit vector so magnitude of \(\vec{a}\) will be 1.
∴|\(\vec{a}\)| = 1
(\(\vec{x}\) – \(\vec{a}\) ) . (\(\vec{x}\) + \(\vec{a}\)) = 12
\(\vec{x}\) . \(\vec{x}\) + \(\vec{x}\) . \(\vec{a}\) – \(\vec{a}\) . \(\vec{x}\) – \(\vec{a}\) . \(\vec{a}\) = 12
|\(\vec{x}\)|² – |\(\vec{x}\)|² = 12
|\(\vec{x}\)|² – (1)² = 12
|\(\vec{x}\)|² = 12 + 1
|\(\vec{x}\)|² = 13
|\(\vec{x}\)| = \(\sqrt{13}\)

Section – C
This section comprises of short answer type questions (SA) of 3 marks each

Question 26.
Find ∫\(\frac{d x}{\sqrt{3-2 x-x^2}}\)
Solution:
We have given I = ∫\(\frac{d x}{\sqrt{3-2 x-x^2}}\)
Now, we can write 3 as 4 – 1
3 – 2x – x² = – x² – 2x + 3
= -(x² + 2x – 3)
= – (x² + 2x + 1 – 4)
= – [(x + 1)² – (2)²]
=2² – (x + 1)²
∴ I = ∫\(\frac{d x}{\sqrt{(2^2) – (x+1)^2}}\)
[ Now this is standard form of a² – x²]
Let t = x + 1
dt = dx
∫\(\frac{d t}{\sqrt{(2^2) – t^2}}\) = sin^-1\(\frac { t }{ 2 }\) + C
( ∵∫\(\frac{d x}{\sqrt{(a^2) – x^2}}\) = sin^-1\(\frac { x }{ a }\) + C)
Now put the value of t, I = sin^-1\(\frac { x + 1}{ 2 }\) + C

Question 27.
Three friends go for coffee. They decide who will pay the bill, by each tossing a coin and then letting the “odd person” pay. There is no odd person if all three tosses produce the same result. If there is no odd person in the first round, they make a second round of tosses and they continue to do so until there is an odd person. What is the probability that exactly three rounds of tosses are made?

OR

Find the mean number of defective items in a sample of two items drawn one-by-one without replacement from an urn containing 6 items, which include 2 defective itmes. Assume that the items are identical in shape and size.
Solution:
P(not obtaining an odd person in a single round) = P(All three of them throw tails or All three of them throw heads)
= \(\frac { 1 }{ 2 }\) x \(\frac { 1 }{ 2 }\) x \(\frac { 1 }{ 2 }\) x 2 = \(\frac { 1 }{ 4 }\)
P(obtaining an odd person in a single round) = 1 – P(not obtaining an odd person in a single round) = \(\frac { 3 }{ 4 }\)
The required probability – P(’In first round there is no odd person’ and ‘In second round there is no odd person’ and ‘In third round there is an odd person’)
= \(\frac { 1 }{ 4 }\) x \(\frac { 1 }{ 4 }\) x \(\frac { 3 }{ 4 }\) = \(\frac { 3 }{ 64 }\)

OR

Let X denote the Random variable defined by the number of defective items.
P (x = 0) = \(\frac { 4 }{ 6 }\) x \(\frac { 3 }{ 5 }\) = \(\frac { 2 }{ 5 }\)
P (x = 1) = 2 x (\(\frac { 2 }{ 6 }\) x \(\frac { 4 }{ 5 }\)) = \(\frac { 8 }{ 15 }\)
P (x = 2) = \(\frac { 2 }{ 6 }\) x \(\frac { 1 }{ 5 }\) = \(\frac { 1 }{ 15 }\)

Mean ∑p_ix_i = \(\frac { 10 }{ 15 }\) = \(\frac { 2 }{ 3 }\)

Question 28.
Evaluate:

OR

Evaluate:

Solution:
Let

Question 29.
Solve the differential equation:
ydx + (x – y²)dy = 0
Solve the differential equation: xdy – ydx = \(\sqrt{x^2+y^2}\) dx
Solution:
We have given differential equation is
ydx + (x – y²)dy = 0
Reducing the given differential equation to the form \(\frac { dy }{ dx }\) + Px = Q
∴ We have to find \(\frac { dy }{ dx }\)
\(\frac { dy }{ dx }\) = \(\frac{y^2-x}{y}\)
\(\frac { dy }{ dx }\) = y – \(\frac { x }{ y }\)
\(\frac { dy }{ dx }\) + \(\frac { x }{ y }\) = y
Now, comparing this with \(\frac { dx }{ dy }\) + Px = Q We get
P = \(\frac { 1 }{ y }\) and Q = y
Now,
I.F. = e^∫pdy
= \(e^{\int \frac{d y}{y}}\)
= e^{log y}
= y
The general solution is given by
x (I.F.) = ∫(Q x I.F.)dy + C
= ∫y x ydy + C
xy = ∫y²dy + C
xy = \(\frac{y^3}{3}\) + C
Which is the required general solution.

OR

We have given differential equation is
xdy – ydx = \(\sqrt{x^2+y^2}\) dx
It is a Homogeneous Equation as
\(\frac { dy }{ dx }\) = \(\frac{\sqrt{x^2+y^2}+y}{x}\) ………………..(i)
Solving \(\frac { dy }{ dx }\) by putting y = 2\(\sqrt{Vx}\)
Differentiating w.r.t.x
\(\frac { dy }{ dx }\) = x \(\frac { dυ }{ dx }\) = \(\frac {υdy }{ dx }\)
\(\frac { dy }{ dx }\) = x \(\frac { dυ }{ dx }\) + υ
Putting value of \(\frac { dy }{ dx }\) and y = υx in (i), we get
x \(\frac { dυ }{ dx }\) + υ = \(\frac{\sqrt{x^2+v^2 x^2}+v x}{2}\)
x \(\frac { dυ }{ dx }\) = \(\sqrt{1+v^2}\) + υ – υ
x \(\frac { dυ }{ dx }\) = \(\sqrt{1+v^2}\)
\(\frac { dυ }{ dx }\) = \(\frac{\sqrt{1+v^2}}{x}\)
\(\frac{d v}{\sqrt{1+v^2}}\) = \(\frac { dx }{ x }\)
Integrating both sides, we get
∫\(\frac{d v}{\sqrt{1+v^2}}\) = ∫\(\frac { dx }{ x }\)
log |υ + \(\sqrt{v^2+1}\) | = log |x| + C
(∵∫\(\frac{d x}{\sqrt{a^2+x^2}}\) = log | x + \(\sqrt{x^2+a^2}\) | + C Putting a = 1, x = υ)
log |υ + \(\sqrt{v^2+1}\) | = log |cx|
υ + \(\sqrt{v^2+1}\) = cx
Putting υ \(\frac { y }{ x }\)
\(\frac { y }{ x }\) + \(\sqrt{\left(\frac{y}{x}\right)^2+1}\) = cx
\(\frac { y }{ x }\) + \(\sqrt{\frac{y^2+x^2}{x^2}}\) = cx
y + \(\sqrt{y^2+x^2}\) = cx²
∴ Required general solution is y + \(\sqrt{y^2+x^2}\) = cx²

Question 30.
Solve the following Linear Programming Problem graphically:
Maximize Z = 400x + 300y subject to x + y ≤ 200, x ≤ 40 , x ≤ 20y ≥ 0
Solution:
Wehave Z = 400x + 300y subject to x + y ≤ 200, x ≤ 40, x ≥ 20y ≥ 0
The corner points of the feasible region are C(20, 0), D(40, 0), B(40, 160), A(20, 180)


Maximum profit occurs at x = 40, y = 160 and the maximum profit ₹ 64,000

Question 31.
Find \(\int \frac{\left(x^3+x+1\right)}{\left(x^2-1\right)}\)
Solution:
I = \(\int \frac{\left(x^3+x+1\right)}{\left(x^2-1\right)}\)
Divide x³ + x + 1, we get
x + \(\frac{2 x+1}{x^2-1}\) = x + \(\frac{2 x+1}{(x+1)(x-1)}\)
(∵(a² – b²) = (a – b) (a + b) )
Now solving \(\frac{2 x+1}{(x+1)(x-1)}\)
We can write it as
\(\frac{2 x+1}{(x+1)(x-1)}\) = \(\frac { A }{ (x – 1) }\) + \(\frac { B }{ (x + 1) }\)
= \(\frac { A(x + 1)+B(x – 1) }{ (x – 1) (x + 1) }\)
By cancelling denominator
2x + 1 = A(x + 1) + B (x – 1) ……………….(i)
Putting x = 1, in equation (i), we get
A = \(\frac { 3 }{ 2 }\)
Similarly putting x = -1, in equation (1), we get
B = \(\frac { 1 }{ 2 }\)
Hence, we can write it as

Section – D
(This section comprises of long answer – type questions (LA) of 5 marks each)

Question 32.
Make a rough sketch of the region {(x, y): 0 ≤ y ≤ x², 0 ≤ y ≤ x, 0 ≤ x ≤ 2} and find the area of the region using integration.
Solution:
We have given
{(x, y): 0 ≤ y ≤ x², 0 ≤ y ≤ x, 0 ≤ x ≤ 2}
Now,
x ≥ 0, y ≥ 0, x ≤ 2
y ≤ x² ……………. (i)
y ≤ x ………………. (ii)
Intersecting point of (i) and (ii) are
x² = x
x² – x = 0
x (x – 1) = 0
x = 0, 1
When x = 0, y = 0
When x = 1, y = 1
Hence the points of intersection of the parabola y = x² and the line y = x are (0,1) and (1,1)
Required Area =

Question 33.
Define the relation R in the set N x N as follows:
For (a, b), (c, d) ∈ N x N, (a, b) R (c, d) iff ad = bc. Prove that R is an equivalence relation in N x N.

OR

Given a non-empty set X, define the relation R in P(X) as follows:
For A, B ∈ P(X), (A, B) ∈ R iff A ⊂ B. Prove that R is reflexive, transitive and not symmetric.
Solution:
Let (a, b) ∈ N N. Then we have ab = ba (by commutative property of multiplication of natural numbers)
= (a, b) R(a, b)
Hence, R is reflexive.
Let (a, b), (c, d) ∈ N x N such that (a, b) R(c, d).
ad = bc
cb = da (by commutative property of multiplication of natural numbers)
(c, d) R(a, b)
Hence, R is symmetric.
Let (a, b), (e, d’), (e, f) ∈ N x N such that
(a, b) R(c, d) and (c, d) R(e,f)
Then ad = bc, cf = de
adcf = bcde
af = be
(a, b) R(e,f)
Hence, R is transitive.
Since, R is reflexive, symmetric and transitive, R is an equivalence relation on N x N.

OR

We have given relation is
R = {(A, B): A and H are sets, A ⊂ B}
Check reflexivity
Since, every set is a subset of itself.
A ⊂ A
∴ (A,A) ∈R
Hence, R is reflexive
Check symmetry
To check symmetric or not,
if (A, B) ∈ R, then (B, A) ∈ R
Let A = {1, 2), B = (1, 2,3)
∴ If (A. B) ∈ R,
A ⊂ B.
But, B ⊂ A is not true (∵ 3 ∉ {1,2})
∴ R is not symmetric
Check transitivity
Since (A, B) ∈ R and (B, C) ∈ R
if,
A⊂B and B⊂C
Then A⊂C
=> (A, C) ∈ R
So, if (A, B) ∈ R and (B, C) ∈ R, then (A,C) ∈ R
∴ R is transitive.

Question 34.
An insect in crawling along the line \(\bar{r}\) = 6\(\hat{i}\) + 2\(\hat{j}\) + 2\(\hat{k}\) + λ(\(\hat{i}\) – 2\(\hat{j}\) + 2\(\hat{k}\)) and another insect is crawling along the line \(\bar{r}\) = – 4 \(\hat{i}\) – \(\hat{k}\) + μ(3\(\hat{i}\) – 2\(\hat{j}\) – 2\(\hat{k}\)) . At what points on the lines should they reach so that the distance betweën them is the shortest? Find the shortest possible distance between them.

OR

The equations of motion of a rocket are:
x = 2t, y – 4t, z = 4t, where the time t is given in seconds, and the coordinates of a moving points in km. What is the path of the rocket? At what distances will the rocket be from the starting point 0(0, 0, 0) and from the following line in 10 seconds?
\(\vec{r}\) = 20\(\hat{i}\) – 10\(\hat{j}\) + 40\(\hat{k}\) + μ(10\(\hat{i}\) – 20\(\hat{j}\) – 10\(\hat{k}\))
Solution:
The given lines are non-parallel lines. There is a unique line segment PQ (Plying on one and Q on the other, which is at right angles to both the lines. PQ is the shortest distance between the line. Hence, the shortest possible distance between the insects = PQ.
The position vector of Plying on the line
\(\vec{r}\) = 6\(\hat{i}\) + 2\(\hat{j}\) + 2\(\hat{k}\) + λ(\(\hat{i}\) – 2\(\hat{j}\) + 2\(\hat{k}\)) is (6+λ)\(\hat{i}\)+(2 – 2λ)\(\hat{j}\) + (2+2λ)\(\hat{k}\) for some λ
The position vector of Q lying on the line
\(\vec{r}\) = – 4\(\hat{i}\) – \(\hat{k}\) + μ(3\(\hat{i}\) – 2\(\hat{j}\) – 2\(\hat{k}\)) is (- 4 + 3μ)\(\hat{i}\) + (- 2μ)\(\hat{j}\) + ( – 1 – 2μ)\(\hat{k}\) for some μ
\(\vec{PQ}\)PQ = ( – 10 + 3μ – λ)\(\hat{i}\) + ( – 2μ – 2 + 2λ)\(\hat{j}\) + ( – 3 – 2μ – 2λ)\(\hat{k}\)
Since, PQ is perpendicular to both the lines ( – 10 + 3μ – λ) + ( – 2μ – 2 + 2λ)(-2) + ( – 3 – 2μ – 2λ)2 = 0
i.e., μ – 3λ = 4 ……………(i)
and( – 10 + 3μ – λ)3+( – 2μ – 2 + 2λ)( – 2) + ( – 3 – 2μ – 2λ)( – 2) = 0
i.e., 17μ – 3λ = 20 ……………….. (ii)
Solving (i) and (ii) for λ and μ, we get μ = 1, λ = -1.
The position vector of the points, at which they should be so that the distance between them is the
shortest, are 5\(\hat{i}\) + 4\(\hat{j}\) and – \(\hat{j}\) – 2\(\hat{j}\) – 3\(\hat{k}\)
\(\vec{PQ}\) = – 6\(\hat{i}\) – 6\(\hat{j}\) – 3\(\hat{k}\)
The shortest distance |\(\vec{PQ}\)| = \(\sqrt{6^2+6^2+3^2}\) = 9

OR

Eliminating t between the equations, we obtain the equation of the path \(\frac { x }{ 2 }\) = \(\frac { y }{ -4 }\) = \(\frac { z }{ 2 }\) which are the equations of the line passing through the origin having direction ratios (2, -4, 4). This line is the path of the rocket.
When t =10 seconds,
The rocket will be at the point (20, – 40, 40).
Hence, the required distance from the origin at 10 seconds
= \(\sqrt{20^2+40^2+40^2}\) = 20 x 3
= 60 km
The distance of the point (20, – 40, 40) from the given line

Question 35.
If

find A^-1 Use A^-1 to solve the following system of equations 2x – 3y + 5z = 11, 3x + 2y – 4z = -5, x + y – 2z = – 3.
Solution:
Given system of linear equations are
2x – 3y + 5z = 11
3x + 2y – 4z = – 5
x + y – 2z = – 3
Represent it in matrix form

which is the form of AX = B

Section – E
This section comprises of 3 case-study/passage-based questions of 4 marks each wkth two sub-parts. First two cese study questions have three sub-parts (i), (ii), (iii) of marks 1, 1, 2 respectively. The third case study question has two sub-parts of 2 marks each.

Question 36.
Case-Study 1: Read the following passage and answer the questions given below:

The temperature of a person during an intestinal illness is given by f(x) = – 0.1x² + mx +98.6,0 ≤ x ≤ 12, m being a constant, where f(x) is the temperature in °F at x days.
(i) Is the function differentiable in the interval (0, 12)? Justify your answer.
(ii) If 6 is the critical point of the function, then find the value of the constant m.
(iii) Find the intervals in which the function is strictly increasing/strictly decreasing.

OR

(iii) Find the points of local maximum/local minimum, if any, in the interval (0, 12) as well as the points of absolute maximum/absolute minimum in the interval [0, 12]. Also, find the corresponding local maximum/local minimum and the absolute maximum/absolute minimum values of the function.
Solution:
(i) f(x) = – 0.1x² + mx + 98.6, being a polynomial function, is differentiable everywhere. Hence, differentiable in (0, 12)

(ii) We have given function
f(x) = – 0.1 x² + mx + 98.6
Differentiate f(x) w.r.t. x
f'(x) = – 0.2 x + m
Since, 6 is the critical point,
f'(6) = 0
-0.2 x 6 x m = 0
m = 1.2

(iii) We have given function
f (x) = – 0.1 x² + mx + 98.6
f'(x) = -0.2x + 1.2
= – 0.2 (x – 6)

OR

(iii) We have given function
f(x) = – 0.1 x² + mx + 98.6
f(x) = – 0.1 x² + 1.2x + 98.6 (∵m = 1.2)
f’(x) = – 0.2x + 1.2, f’(6) = 0
∴ f”(x) = – 0.2
∴ f”(6) = – 0.2 < 0

Hence, by second derivative test 6 is a point of local maximum. The local maximum value is
f(6) = – 0.1 x 6² + 1.2 x 6 + 98.6 = 102.2
We have f(0) = 98.6, f(6) = 102.2, f(12) = 98.6
6 is the point of absolute maximum and the absolute maximum value of the function = 102.2
0 and 12 both are the points of absolute maximum and the absolute minimum value of the function
= 98.6

Question 37.
Case-study 2: Read the following passage and answer the questions given below:

In an elliptical sport field the authority wants to design a rectangular soccer field with the maximum possible area. The sport field is given by the graph of \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1.
(i) If the length and the breadth of the rectangular field be 2x and 2y respectively, then find the area function in terms of x.
(ii) Find the critical point of the function.
(iii) Use First derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b)
that maximize its area.

OR

(iii) Use Second Derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b) that maximize its area.
Solution:
(i) Let (x, y) = \(\left(x, \frac{b}{a} \sqrt{a^2-x^2}\right)\) be the upper right vertex of the rectangle.
The area function A = 2x + 2\(\frac { b }{ a }\) \(\sqrt{a^2-x^2}\) ……………. (i)
= \(\frac { 4b }{ a }\) x \(\sqrt{a^2-x^2}\) x ∈ (0,a)

(ii) Differentiate (i) w.r.t. x, we get

(iii) For the values of \(\frac{a}{\sqrt{2}}\) less than and close to a\(\sqrt{2}\),\(\frac { dA }{ dx }\) >0 and for the values of x greater than \(\frac{a}{\sqrt{2}}\) and close to \(\frac{a}{\sqrt{2}}\), \(\frac { dA }{ dx }\) <0.
Hence, by the first derivative test,
There is a local maximum at the critical point x = \(\frac{a}{\sqrt{2}}\). Since there is only one critical point.
∴The area of the soccer field is maximum at this critical point x = \(\frac{a}{\sqrt{2}}\)
Thus, for maximum area of the soccer field, its length should be a\(\sqrt{2}\) and its width should be b\(\sqrt{2}\).

OR

(iii) A = 2x x 2\(\frac { b }{ a }\)\(\sqrt{a^2-x^2}\), x ∈ (0, a)
Squaring both sides, we get

A is maximum when Z is maximum.

Hence, by the second derivative test, there is a local maximum value of Z at the critical point x = \(\frac{a}{\sqrt{2}}\).
Since, there is only one critical point, therefore, Z is maximum at x = \(\frac{a}{\sqrt{2}}\), hence, A is maximum at x = \(\frac{a}{\sqrt{2}}\)
Thus, for maximum area of the soccer field, its length should be a\(\sqrt{2}\) and its width should be b\(\sqrt{2}\).

Question 38.
Case-Study 3: Read the following passage and answer the questions given below:

There are two antiaircraft guns, named as A and B. The probabilities that the shell fired from them hits an airplane are 0.3 and 0.2 respectively. Both of them fired one shell at an airplane at the same time.
(i) What is the probability that the shell fired from exactly one of them hit the plane?
(ii) If it is known that the shell fired from exactly one of them hit the plane, then what is the probability that it was fired from B?
Solution:
(i) Let P be the event that the shell fired from A hits the plane and Q be the event that the shell fired from B hits the plane. The following four hypotheses are possible before the trial, with the guns operating independently.
E₁ = PQ, E₂ = \(\overline{\mathrm{P}} \overline{\mathrm{Q}}\), E₃ \(\bar{P}\)Q, E₄ = P\(\bar{Q}\)
Let E = The shell fired from exactly one of them hits the plane.
P(E₁) = 0.3 x 0.2 = 0.06, P(E₂) = 0.7 x 0.8 = 0.56, P(E₃) = 0.7 x 0.2 = 0.14, P(E₄) = 0.3 x 0.8 = 0.24
P\(\left(\frac{E}{E_1}\right)\) = 0, P\(\left(\frac{E}{E_2}\right)\) = 0, P\(\left(\frac{E}{E_3}\right)\) = 1, P\(\left(\frac{E}{E_4}\right)\) = 1
P(E) = P(E₁).P\(\left(\frac{E}{E_1}\right)\) + P(E₂).P\(\left(\frac{E}{E_2}\right)\) + P(E₃).P\(\left(\frac{E}{E_3}\right)\) + P(E₄).P\(\left(\frac{E}{E_4}\right)\)
= 0.14 + 0.24
= 0.38

(ii) By Bayes’ Theorem