CBSE Sample Papers for Class 10 Maths Standard Set 6 with Solutions

Practicing the CBSE Sample Papers for Class 10 Maths Standard Set 6 allows you to get rid of exam fear and be confident to appear for the exam.

CBSE Sample Papers for Class 10 Maths Standard Set 6 with Solutions

Section – A

Question 1.
What are the coordinates of the centroid of triangle with vertices A(2, 3), B(4, 7) and C(6, 2)?
(a) (4, 4)
(b) (4, 3)
(c) (3, 4)
(d) (3, 3)
Answer:
(a) (4, 4)
Explanation: Given : A(2, 3), B(4, 7) and C(6, 2).

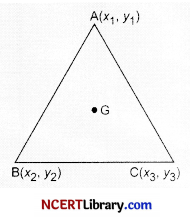
We know that,
Centroid (G) = \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)
= \(\left(\frac{2+4+6}{3}, \frac{3+7+2}{3}\right)\)
= (4, 4)

Question 2.
In what ratio does the line x – y – 2 = 0 divides the line segment joining (3, – 1) and (8, 9)?
(a) 3 : 3
(b) 2 : 3
(c) 3 : 2
(d) 3 : 4
Answer:
(b) 2 : 3
Explanation: Let P be the point that divides the line segment joining (3, – 1) and (8, 9) in ratio k : 1.
Then, coordinates of point P is given by using internal section formula,
p (x , y) = \(\left[\frac{8 k+3}{k+1}, \frac{9 k-1}{k+1}\right]\)
Since, point P lies on line x – y – 2 = 0, soP must satisfy the above equation.
Putting x = \(\frac{8 k+3}{k+1}\), y = \(\frac{9 k- 1}{k+1}\) in equation x – y – 2 = 0, we get
\(\frac{8 k+3}{k+1}\) – \(\left(\frac{9 k-1}{k+1}\right)\)] – 2 = 0
⇒ \(\frac{8 k+3-9 k+1-2 k-2}{k+1}\) = 0
⇒ \(\frac{-3 k+2}{k+1}\) = 0
⇒ -3 k + 2 = 0
⇒ k = \(\frac { 2 }{ 3 }\)
⇒ k : 1 = \(\frac { 2 }{ 3 }\) : 1 ⇒ 2 : 3
Hence, the required ratio is 2 : 3.

Question 3.
A man goes 15 m due west and then 8 m due north. What is distance from the starting point:
(a) 17.0 m
(b) 17.5 m
(c) 16.9 m
(d) 16.5 m
Answer:
(a) 17.0 m
Explanation: Let the initial position of the man be A and his final position be C. Since, the man goes 15 m due west and then 8 m due north.

Therefore, ABAC is a right triangle right angled at B, such that
AB = 1.5 m and BC = 8 m
By Pythagoras theorem, we have
AC² = AB² + BC²
⇒ AC² = (15)² + (8)²
⇒ AC² = 225 + 64
⇒ AC² = 289
⇒ AC = 17 m
Hence, the man is at a distance of 17 m from the starting point.

Question 4.
In a triangle ABC, AB = AC = 25 cm, and BC = 14 cm, then find the altitude from A on BC:
(a) 22 cm
(b) 26 cm
(c) 24 cm
(d) 27 cm
Answer:
(c) 24 cm
Explanation: Given, ABC is a isosceles triangle.
AB AC = 25 cm and BC = 14 cm
Draw AD ⊥ BC. Then, D is the mid, point of BC.
⇒ BC = \(\frac { 1 }{ 2 }\) = \(\frac { 1 }{ 2 }\) = 7 cm

Since, △ABD is a right triangle right angled at D.
∴ AB² = AD² + BD²
⇒ (25)² = AD² + (7)²
⇒ AD² = (25)² – (7)²
= 625 – 49 = 576
⇒ AD = √576 = 24 cm
Hence, altitude AD = 24 cm.

Question 5.
In the given figure, if ∠AOD = 135°, then ∠BOC is equal to:

(a) 52.5°
(b) 45°
(c) 62.5°
(d) 25°
Answer:
(b) 45°
Explanation: Given, ∠AOD = 135°
∠BOC = 180° – 135° = 45°
Since, angle subtended at the centre by a pair of opposite sides are supplementary.

Question 6.
A wheel makes 1000 revolutions in covering a distance of 88 km. Find the radius of the wheel:
(a) 11 m
(b) 14 m
(c) 12 m
(d) 10 m
Answer:
(b) 14 cm
Explanation: Distance covered in one revolution
= \(\frac{88 \times 1000}{1000}\) m = 88 m
2πR = 88 ⇒ 2 × \(\frac { 1 }{ 2 }\) × R = 88 m
R = \(\left(88 \times \frac{7}{44}\right)\) = 14 m.

Question 7.
For what value of k is – 4 a zero of the polynomial f(x) = x² – x – (2k + 2)?
(a) 6
(b) – 6
(c) 9
(d) – 9
Answer:
(c) 9
Explanation: f(x) = x² – x – (2k + 2)
Substituting x for – 4, we have f(- 4) = (- 4)² – (- 4) – (2k + 2)
= 16 + 4 – 2k – 2
= 18 – 2k = 0
Thus, 18 – 2k = 0
or
2k = 18 or k = 9.

Question 8.
If triangle ABC is right angled at C, then find the value of cos (A + B):
(a) cos 60°
(b) cos 30°
(c) cos 90°
(d) cos 180°
Answer:
(c) cos 90°
Explanation: Given, △ABC is right angled at C. i.e., ∠C =90°

Then by triangle angle sum property
∠A + ∠B + ∠C =180°
⇒ ∠A + ∠B + 90° = 180°
⇒ ∠A + ∠B =180°- 90°
⇒ ∠A + ∠B = 90°
Taking cos on both the sides, we get
cos (A + B) = cos 90°
cos (A + B) = 0

Question 9.
Given that tan A = \(\frac { 1 }{ √5 }\), what is the value of \(\frac{cosec^2 A-sec ^2 A}{{cosec}^2 A+sec ^2 A}\)?
(a) \(\frac { 5 }{ 3 }\)
(b) \(\frac { 2 }{ 3 }\)
(c) \(\frac { 3 }{ 2 }\)
(d) \(\frac { 5 }{ 2 }\)
Answer:
(b) \(\frac { 2 }{ 3 }\)
Explanation:

Question 10.
Find the value of 9 sec² A – 9 tan² A.
(a) 8
(b) 10
(c) 9
(d) 7
Answer:
(c) 9
Explanation: We have
9 sec²A – 9 tan²A = 9(sec²A – tan²A) = 9 × 1 = 9 [∵ sec²θ = 1 + tan²θ]

Question 11.
For what value of k, are the roots of the quadratic equation kx(x -2) + 6 = 0 equal?
(a) 6
(b) 9
(c) 7
(d) 8
Answer:
(a) 6
Explanation: Given quadratic equation is,
kx(x – 2) + 6 =0
⇒ kx² – 2 kx + 6 = 0
On comparing the above equation with ax² + bx + c = 0, we get
a = k, b = – 2k, c = 6
For equal roots,
D = b² – 4ac = 0
⇒ (- 2k)2 -4 x 1 x 6 = 0
⇒ 4k2 – 24k = 0
⇒ 4k(k — 6) = 0
⇒ k = 0 (not possible) or k = 6
k = 6

Question 12.
ABC is a right angled triangle, right angled at B such that BC = 6 cm, AB = 8 cm and AC = 10 cm. A circle with centre O is incribed in △ABC. The radius of the circle is:
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm
Answer:
(b) 2 cm
Explanation: An incircle is drawn with centre O which touches the sides of the triangle ABC at P, Q and R. OP, OQ and OR are radii and AB, BC and CA are the tangents to the circle.
OP ⊥ AB, OQ ⊥ BC and OR ⊥ CA.
OPBQ is a square. (∴∠B = 90°)

Let r be the radius of the circle
∴ PB = BQ = r
AR = AP = 8 – r,
CQ = CR = 6 – r
AC = AR + CR
⇒ 10 = 8 – r + 6 – r
⇒ 10 = 14 – 2r
⇒ 2r = 14 – 10 = 4
⇒ r = 2
∴ Radius of the incircle = 2 cm.

Question 13.
If the pair of linear equations 2x + 3y = 11 and (m + n) x + (2m – n) y – 33 = 0 has infinitely many solutions, then the values of m and n, are ………. and ………. respectively.
(a) 5, 1
(b) 1, 2
(c) – 1, 5
(d) 1, – 5
Answer:
(a) 5, 1
Explanation: It has infinite many solution
So, \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
⇒ \(\frac{2}{m+n}\) = \(\frac{3}{2m-n}\) = \(\frac { 11 }{ 33 }\)
⇒ \(\frac{2}{m+n}\) = \(\frac{3}{2m-n}\) = \(\frac { 1 }{ 3 }\)
⇒ \(\frac{2}{m+n}\) = \(\frac { 1 }{ 3 }\)
⇒ m + n = 6 ….(i)
and 2m – n = 9 ….(ii)
on adding 3m = 15
⇒ m = 5
Putting m in equation (i), 5 + n = 6
⇒ n = 1.

Question 14.
Write the sum and product of the zeroes of the quadratic polynomial x² + 7x + 10.
(a) 19, – 8
(b) 13, 12
(c) – 7, 10
(d) 11, – 2
Answer:
(c) – 7, 10
Explanation: Given quadratic polynomial is ,x² + 7x + 10
Here a = 1, b = 7 and c = 10
We know, sum of roots (α + β) = \(\frac { – b }{ a }\)
α + β = \(\frac { – 7 }{ 1 }\) = – 7
Product of roots (αβ) = \(\frac { c }{ a }\)
αβ = \(\frac { 10 }{ 1 }\) = 10

Question 15.
If α and β are the zeroes of the polynomial f(y) = 2y² + 7y + 5 write the values of α + β + αβ.
(a) 1
(b) 0
(c) -2
(d) -1
Answer:
(d) -1
Explanation: Given, f(y) = 2y² + 7y + 5
Here α + β = –\(\frac { 7 }{ 2 }\), (∵ α + β = \(\frac { – b }{ a }\))
αβ = \(\frac { 5 }{ 2 }\) (∵ α + β = \(\frac { c }{ a }\))
∴ (α + β) + (αβ) = –\(\frac { 7 }{ 2 }\) + \(\frac { 5 }{ 2 }\) = -1.

Question 16.
In the given figure, PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB = 10 cm and CQ = 2 cm, what is the length of PC?

(a) 6 cm
(b) 8 cm
(c) 10 cm
(d) 7 cm
Answer:
(b) 8 cm
Explanation:
Given: PA and PB are tangents to the circle having centre O.

Now, PA = 10 [∵ PB = 10 cm (Given)]
⇒ PC + AC = 10
⇒ PC + CQ = 10 [∵AC and CQ are tangents from the point C]
⇒ PC + 2 = 10 [∵CQ = 2 cm (Given)]
⇒ PC = 10 – 2 = 8
∴ PC = 8 cm

Question 17.
A box contains 90 discs, numbered from 1 to 90. If one disc is drawn at random from the box, the probability that it bears a prime number less than 23 is:
(a) \(\frac { 7 }{ 90 }\)
(b) \(\frac { 10 }{ 90 }\)
(c) \(\frac { 4 }{ 45 }\)
(d) \(\frac { 9 }{ 89 }\)
Answer:
(c) \(\frac { 4 }{ 45 }\)
Explanation: Total number of possible outcomes = 90
Thus, the favourable outcomes are 2, 3, 5, 7, 11, 13, 17, 19.
Hence, the total number of favourable outcomes = 8
P(E) = \(\frac { 8 }{ 90 }\) = \(\frac { 4 }{ 45 }\)

Question 18.
What is the probability that two friends have different birthdays?
(a) \(\frac { 1 }{ 365 }\)
(b) \(\frac { 2 }{ 365 }\)
(c) \(\frac { 364 }{ 365 }\)
(d) \(\frac { 363 }{ 365 }\)
Answer:
(c) \(\frac { 364 }{ 365 }\)
Explanation:
Explanation: If
Total number of possible outcomes = 365 × 365
Total number of favourable outcomes = 365 × (365 – 1)
∴ P(E) = \(\frac{365 \times 364}{365 \times 365}\) = \(\frac { 364 }{ 365 }\)

Question 19.
DIRECTION: In the question number 19 and 20, a statement of assertion (A) is followed by a statement of Reason(R).
Choose the correct option:
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A)
(b) Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A)
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Each question consists of two statements, namely, Assertion (A) and Reason (R). For selecting the correct answer : use the following code :
Statement A (Assertion): Consider the following distribution :

Class interval	Frequency
3-6	2
6-9	5
9-12	21
12-15	23
15-18	10
18-21	12

The mode of the above is 12.4.
Statement R (Reason): The value of the variable which occurs most often is the mode.
Answer:
(a) Both the Assertion and the Reason are correct and the Reason is the correct explanation of the Assertion.
Explanation: Maximum frequency = 23
Hence, modal class is 12 – 15
Now, Mode = l + \(\frac{\left(f_k-f_{k-1}\right)}{2 f_k-f_{k-1}-f_{k+1}}\) × h
= 12 + \(\left(\frac{23-21}{46-21-10}\right)\) × 3
= 12 + \(\frac{6}{46-31}\)
= 12 + \(\frac{6}{15}\) = 12.4

Question 20.
Statement A (Assertion): In a cricket match a batsman hits a boundary 9 times out of 45 balls he plays. The probability that in a given throw he does not hit the boundary is 4/5.
Statement R (Reason): P(E) + P (not E) = 1.
Answer:
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A)
Explanation: For reason, as per the empirical formula
The sum of all the probabilities of all possible outcomes of experiment is 1.
P(Event) + P (not an Event) = 1
So, reason is true.
For assertion,
As per the description P(boundary) or P(E) = \(\frac{9}{45}\) = \(\frac{1}{5}\)
So P(no boundary) or P(not E) = \(\frac{1 – 1}{5}\) = \(\frac{4}{5}\)
So, assertion is also true and Reason is the correct explanation of the assertion.

Section – B

Question 21.
A student write four pair of linear equations in two variables on his copy as given below :
(a) 3x – y = 9, .x – \(\frac{y}{3}\) = 3
(b) 4x + 3y = 24, -2x + 3y = 6
(c) 5x – y = 10, 10x – 2y = 20
(d) -2x + y = 3, -4x + 2y = 10
(i) Flow many pair of linear equations are consistent?
(ii) Which pair of linear equations are inconsistent?
Answer:
On comparing the given equations with standard form of pair of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we get
(a) \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\) as \(\frac{3}{1}\) = \(\frac{3}{1}\) = \(\frac{-9}{1}\), consistant
(b) \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\) as \(\frac{4}{-2}\) ≠ – 1, consistant
(c) \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\) as \(\frac{5}{10}\) = \(\frac{1}{2}\) = \(\frac{10}{20}\), consistant
(d) \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\) as \(\frac{-2}{-4}\) = \(\frac{1}{2}\) ≠ \(\frac{3}{10}\), consistant

(i) So, three pair of linear equations are consistent.
(ii) Fourth pair of linear equations is inconsistent.

Question 22.
Find a point on the Y-axis which is equidistant from the points A(- 4, 3) and B(6, 5).
OR
The line segment joining the points A(3, – 4) and B(1,2) is trisected at the points P(p, – 2) and Q\(\left(\frac{5}{3}, q\right)\). Find the value of p and q.
Answer:
Let P be the required point on X-axis.
∴ P(0,y)
Now, PA = PB [Given]
∴ \(\sqrt{(0+4)^2+(y-3)^2}\) = \(\sqrt{(0-6)^2+(y-5)^2}\) [using distance formula]

On squaring both sides,
(4)² + (y – 3)² = (6)² + (y – 5)²
⇒ 16 + y² – 6y + 9 = 36 + y² 10y + 25
⇒ – 6y + 25 = 61 – 10y
⇒ – 6y + 10y = 61 – 25
⇒ 4y = 36
⇒ y = 9
∴ Coordinates of the point P = (0, 9)
Given : A = (3, -4), B = (1, 2), P = (p, -2) and Q = \(\left(\frac{5}{3}, q\right)\)

Now, AP = PQ + QB
Thus AP : PB = 1 : 2 and AQ : QB = 2 : 1
∴ p = \(\frac{1+3(2)}{1+2}\)
and q = \(\frac{2(2)+1(-4)}{1+2}\)
∴ p = \(\frac{7}{3}\) and q = 0.

Question 23.
A card is drawn from a well-shuffled deck of 52 playing cards. Find the probability of getting:
(i) a black king or a red queen,
(ii) a non-face card.
Answer:
Total number of cards = 52
∴ n(S) = 52
(i) Number of black king or red queen = 2 + 2 = 4
∴ n(A) = 4
P(A) = \(\frac{n(\mathrm{~A})}{n(\mathrm{~S})}\) = \(\frac{4}{52}\) = \(\frac{1}{13}\)

(ii) Number of non-face cards = Total cards – number of face cards
= 52 – 12 = 40
∴ n(B) = 40
P(B) = \(\frac{n(\mathrm{~B})}{n(\mathrm{~S})}\) = \(\frac{40}{52}\) = \(\frac{10}{13}\)

Question 24.
Which term of the sequence 114, 109, 104, ……………, is its first negative term?
OR
If the sum of the first n terms of an A.P. is given as S_n = n(4n + 1), then find its 6th term.
Answer:
Given sequence is 114,109,104, ………………
Here, first term (a)=114
Common difference (d) = 109 – 114 = – 5
Let nth term be the first negative term of the given A.P.
∴ a_n < 0
⇒ a + (n – 1)d < 0
⇒ 114 + (n – 1) (- 5) < 0
⇒ 114 – 5n + 5 < 0
⇒ 119 – 5n < 0
⇒ 119 < 5n ⇒ n > \(\frac { 119 }{ 5 }\)
⇒ n > 23.8
∴ 24th term is the first negative term of the given A.P.
OR
Given: S_n = n(4n + 1)
So, S_{n – 1} = (n – 1) {4(n – 1) + 1}
= (n – 1) (4n – 4 + 1)
= (n – 1) (4n – 3)
Now, nth term of a A.P. is given as,
T_n = S_n – S_{n – 1}
= n(4n + 1) – (n – 1) (4n – 3)
= 4n² + n – 4n² + 7n – 3
= 8n – 3
∴ T₆ = 8 (6) – 3 = 45

Question 25.
The x-coordinates of a point P is twice its y-coordinate. If P is equidistant from Q(2, -5) and R(-3, 6), find the coordinates of P.
Answer:
Let the coordinates of point P be (2y, y). Since, P is equidistant from Q and R
∴ PQ = PR
⇒ \(\sqrt{(2 y-2)^2+(y+5)^2}\) = \(\sqrt{(2 y+3)^2+(y-6)^2}\)
⇒ (2y – 2)² + (y + 5)² = (2y + 3)² + (y – 6)²
⇒ 4y² + 4 – 8y + y² + 25 + 10y = 4y² + 9 + 12y + y² + 36 – 12y
⇒ 2y + 29 = 45
⇒ y = \(\frac { 16 }{ 2 }\) = 8

Section – C

Question 26.
Prove that 3 – √5 is an irrational number.
Answer:
Let us suppose that 3 – √5 is a rational number.
Then, it can be represented in \(\frac { p }{ q }\) form i.e.,
3 – √5 = \(\frac { p }{ q }\) [Where p and q are real numbers and q ≠ o]
⇒ 3 – \(\frac { p }{ q }\) = √5
⇒ \(\frac{3 q-p}{q}\) = √5
∵p and q are real numbers.
Therefore, \(\frac{3 q-p}{q}\) should also be a real number.
But we already know that √5 is an irrational number.
So, our assumption is wrong.
Hence, 3 – √5 is an irrational number.

Question 27.
The LCM of two numbers is M times their HCF. The sum of LCM and HCF is 750. if one number is 250, then find the other number.
Answer:
Let, HCF be ‘H’
then LCM = 14H
sum of LCM and HCF is 750.
∴ 14 H + H = 750
⇒ 15 H = 750
⇒ H = \(\frac { 750 }{ 15 }\)
⇒ H = 50
∴ LCM = 14 H
= 14 × 50 = 700
We know,
Product of LCM and HCF= Product of two numbers Let other number
Let other numbert be y. 700 × 50 = 250 × y
y = \(\frac{700 \times 50}{250}\)
y =140
Hence, the other number is 140.

Question 28.
If a and p are the zeros of the quadratic polynomial f(x) = x² – p(x + 1) – c, then show that (β + 1) (α + 1) = 1 – c.
Answer:
Given : The quadratic polynomial is f(x) = x² – p(x + 1) – c
And α and β are the zeros of the given polynomial.
We know that, sum of the zeros = – \(\frac{\text { Coefficient of x }}{\text { Coefficient of x^2 }}\)
α + β = – \(\frac{(-p)}{1}\)
α + β = p
and αβ = \(\frac{(- p – c)}{1}\)
αβ = – (p + c)
Now L.H.S. = (α + 1) (α + 1)
= αβ + (α + β) + 1
= – (p + c) + p + 1
= – p – c + p + 1
= 1 – c
= R.H.S.

Question 29.
If the mth term of A.P. is \(\frac { 1 }{ n }\) and the nth term is \(\frac { 1 }{ m }\), show that the sum of mn terms is \(\frac { 1 }{ 2 }\)(mn +1).
Answer:
Let, a be the first term and d be the common difference of the given A.P. Then,
a_m = \(\frac { 1 }{ n }\)
a + (m – 1)d = \(\frac { 1 }{ n }\) ….(i)
and a_n = \(\frac { 1 }{ m }\)
a + (n – 1)d = \(\frac { 1 }{ m }\) …..(ii)
subtracting equation (ii) from equation (i), we get
(m – n)d = latex]\frac { 1 }{ n }[/latex] – \(\frac { 1 }{ m }\)
(m – n)d = \(\frac{m-n}{m n}\)
d = \(\frac { 1 }{ mn }\)

Putting d = \(\frac { 1 }{ mn }\) in equation (i), we get
a + (m – 1)\(\frac { 1 }{ m }\) = \(\frac { 1 }{ n }\)
a = \(\frac { 1 }{ mn }\)
∴ S_mn = \(\frac { mn }{ 2 }\) [2a + (mn – 1)d]
S_mn = \(\frac { mn }{ 2 }\) {\(\frac { 2 }{ mn }\) + (mn – 1) \(\frac {1 }{ mn }\)}
S_mn = \(\frac { 1 }{ 2 }\) (mn + 1)

Question 30.
In △ABC, DE || BC such that AD = (4x – 3) cm, AE = (8x – 7) cm, BD = (3x – 1) cm and CE = (5x – 3) cm. Find the value of x.
OR
The diagonals of a quadrilateral ABCD intersect each other at the point O such that = \(\frac{\mathrm{AO}}{\mathrm{OC}}\) = \(\frac{\mathrm{BO}}{\mathrm{OD}}\) Show that ABCD is a trapezium.
Answer:
In △ABC, we have
DE || BC
So, \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\) [Thales’ theorem]

⇒ \(\frac{4 x-3}{3 x-1}\) = \(\frac{8 x – 7}{5 x- 3}\)
⇒ (4x – 3)(5x – 3) = (8x – 7)(3x – 1)
⇒ 20x² – 15x – 12x + 9 = 24² – 21x – 8x + 7
⇒ 4x² – 2x – 2 = 0
⇒ 2x² – x – 1 = 0
⇒ 2x² – 2x + x – 1 = 0
⇒ 2x(x – 1) + 1 (x – 1) = 0
⇒ (x – 1)(2x + 1) = 0
⇒ x = 1
So, the value of x = 1
OR
Let EO || DC meet AD at E.
So, \(\frac{\mathrm{AO}}{\mathrm{OC}}\) = \(\frac{\mathrm{AE}}{\mathrm{ED}}\) [Thales’ theorem] ….(i)
But \(\frac{\mathrm{AO}}{\mathrm{OC}}\) = \(\frac{\mathrm{BO}}{\mathrm{OD}}\) [Thales’ theorem] [Given] ….(ii)
By (i) and (ii),
So, \(\frac{\mathrm{BO}}{\mathrm{OD}}\) = \(\frac{\mathrm{AE}}{\mathrm{ED}}\)

Hence, \(\frac{\mathrm{BO}}{\mathrm{OD}}\) = \(\frac{\mathrm{AE}}{\mathrm{ED}}\) and BO, OD, AE and ED are segments of △DAB.
So, EO || AB
But EO || DC
Thus, AB || DC
As there are only two parallel sides in this quadrilateral, it is a trapezium.

Question 31.
The radii of two concentric circles are 13 cm and 8 cm. PQ is a diameter of the bigger circle. QR is a tangent to the smaller circle touching it at R. Find the length PR.
OR
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Answer:
Let the line QR intersects the bigger circle at S.
Join PS.

O is the mid-point of PQ. [∵ PQ is a diameter of the bigger circle]
QR is a tangent to the smaller circle and OR is a radius through the point of contact R.
∴ OR ⊥ QR ⇒ OR ⊥ QS
Since, OR is perpendicular to a chord QS of the bigger circle.
∴ QR = RS [∵ Perpendicular from the centre to a chord bisects the chord]
⇒ R is the mid-point of QS.
∴ In △QSP, O is the mid-point of PQ and R is the mid-point of QS.
∴ OR = \(\frac { 1 }{ 2 }\)PS
[∵ segment joining the mid-points of any two sides of a triangle is half of the third side]
⇒ PS = 2OR = 2 × 8 cm = 16 cm
In right △OQR, OR² + OR² = OQ²
⇒ 8² + QR² = 13²
⇒ 64 + QR² = 169
⇒ QR² = 169 – 64 = 105
⇒ QR = √105
∴ RS = QR = √105
In △PRS, PR² + RS² = PS²
= (√105)² + 16²
⇒ PR = 19 cm.
OR
Let P be the external point from which tangents PA and PB are drawn on the circle with centre O. Thus, OB is perpendicular to PB and OA is perpendicular to PA.

Hence, ∠OBP = ∠OAP = 90°
In △POB and △POA, OA = OB [Radii of the circle]
OP = OP [common side]
∠OBP = ∠OAP [Each 90°]
∴ △POB ≅ △POA [S.A.S.]
So, PA = PB [By C.P.C.T.]

Section – D

Question 32.
Raju went to a Diwali funfair and stopped at a stall of spinning an arrow. Shopkeeper told him that arrow come to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 and these are equally likely outcomes.
(i) What is the probability that it will point at 8?
(ii) What is the probability that it will point at an odd number?
(iii) What is the probability that it will point at a prime number?
OR
FA piggy bank contains hundred 50 p coins, fifty ₹ 1 coins, twenty ₹ 2 coins and ten ₹ 5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, find the probability that the coin which fell (i) will be a 50p coin, (ii) will be of value more than ₹ 1, (iii) will be value less than ₹ 5, and (iv) will be a ₹ 1 or ₹ 2 coin.
Answer:
Total outcomes = [1, 2, 3, 4, 5, 6, 7, 8]
⇒ n (S) = 8
(i) Let A be the event that arrow will point at 8.
∴ A = {8}
⇒ n (A) = 1
∵ P (A) = \(\frac { 1 }{ 8 }\)

(ii) Let B be the event that arrow will point at an odd number.
∴ B = [1, 3, 5, 7}
⇒ n(B) = 4
∴ P(B) = \(\frac { 4 }{ 8 }\) = \(\frac { 1 }{ 2 }\)

(iii) Let C be the event that arrow will point at a prime number.
∴ C = {2, 3, 5, 7}
⇒ n (C) = 4
∵ P(C) = \(\frac { 4 }{ 8 }\) = \(\frac { 1 }{ 2 }\)
OR
Total number of coins = (100 + 50 + 20 + 10) = 180
(i) Possible number of outcomes of a 50 p coin falling out = 100
Hence, P(E) = \(\frac { 100 }{ 180 }\) = \(\frac { 5 }{ 9 }\)

(ii) Possible number of outcomes of a coin falling out having value more than ₹ 1 = (20 + 10) = 30
Hence, P(E) = \(\frac { 30 }{ 180 }\) = \(\frac { 1 }{ 6 }\)

(iii) Possible number of outcomes of a coin falling out having value less than ₹ 5 = (100 + 50 + 20): 170
Hence, P(E) = \(\frac { 170 }{ 180 }\) = \(\frac { 17 }{ 18 }\)

(iv) Possible number of outcomes of a coin falling out having value either ₹ 1 or ₹ 2 = (50 + 20) = 70
Hence, P(E) = \(\frac { 70 }{ 180 }\) = \(\frac { 7 }{ 18 }\)

Question 33.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac{\mathrm{AO}}{\mathrm{BO}}\) = \(\frac{\mathrm{CO}}{\mathrm{DO}}\) Show that ABCD is a trapezium.
Answer:
Given : A quadrilateral ABCD in which AC and BD are diagonals, which intersect each other at O.
To prove : ABCD is a trapezium such that AB || DC.
Construction: Draw a line OM || AB.
Proof : In △ADB, we have
OM || AB
Therefore, by using basic proportionality theorem, we have

\(\frac{\mathrm{DM}}{\mathrm{MA}}\) = \(\frac{\mathrm{DO}}{\mathrm{OB}}\)
⇒ \(\frac{\mathrm{AM}}{\mathrm{DM}}\) = \(\frac{\mathrm{OB}}{\mathrm{OD}}\) [Taking reciprocals of both sides] …(i)
It is given that \(\frac{\mathrm{AO}}{\mathrm{BO}}\) = \(\frac{\mathrm{CO}}{\mathrm{DO}}\)
⇒ \(\frac{\mathrm{AO}}{\mathrm{OC}}\) = \(\frac{\mathrm{OB}}{\mathrm{OD}}\)
Comparing equations (i) and (ii), we get
\(\frac{\mathrm{AM}}{\mathrm{DM}}\) = \(\frac{\mathrm{OA}}{\mathrm{OC}}\)
Therefore, by using converse of basic proportionality theorem, we have
OM || DC
But OM || AB
⇒ AB || DC
Hence, ABCD is a trapezium.

Question 34.
(a) In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2cm, find the shaded region.

(b) A chord PQ of a circle of radius 10 cm subtends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
Answer:
(a) Area of shaded region = Area of quadrant OACB – Area of △ODB
= \(\frac { 1 }{ 4 }\) πr² – \(\frac { 1 }{ 2 }\) × OD × OB
= \(\frac { 1 }{ 4 }\) × \(\frac { 22 }{ 7 }\) × (3.5)² – \(\frac { 22 }{ 7 }\) × 2 × 3.5
= 9.625 – 3.5
= 6.125 cm².

(b) Given: Radius of circle, r = 10 cm angle, θ = 60°.
Area of minor segment = Area of sector OPQ – Area of △POQ

∴ Area of minor segment = 9.080 cm²
Area of major segment = Area of circle – Area of minor segment = πr² – 9.080
= \(\frac { 22 }{ 7 }\) × 10 × 10 – 9.08
= 314.285 – 9.080
= 305.205 cm²

Question 35.
Check graphically whether the pair of equations 3x – 2y + 2 = 0 and \(\frac { 3 }{ 2 }\) x – y + 3 = 0 is consistent. Also find the coordinates of the points where the graphs of the equations meet the Y-axis.
OR
Solve the following system of linear equations graphically: x – y + 1 = 0 and 3x + 2y – 12 = 0. Calculate the area of the region bounded by these lines and the X-axis.
Answer:
Let XOX’ and YOY’ be the X-axis and Y-axis respectively.
Now, 3x – 2y + 2 = 0 ⇒ 3x = 2y – 2
⇒ x = \(\frac{2(y-1)}{3}\)
If y = – 2, x = – 2
If y = 1,x = 0
If y = 4, x = 2
Therefore,

x	– 2	0	2
y	– 2	1	4

Thus, plotting the points P(- 2, – 2), Q(0, 1) and R(2, 4) on the graph paper, we get the graph of 3x – 2y + 2 = 0, which is represented by PR.
Now, \(\frac{ 3 }{ 2 }\) x – y + 3 = 0 ⇒ 3x – 2y + 6 = 0
y = \(\frac{3(x+2)}{2}\)
If x = 0, y = 3
If x = -2, y = o
If x = -4, y = – 3
Therefore,

X	0	– 2	– 4
Y	3	0	– 3

Thus, plotting the points S(0, 3), T(- 2, 0) and U(- 4, – 3) on the graph paper, we get the graph of \(\frac{ 3 }{ 2 }\)x – y + 3 = 0, which is represented by SU.

Since, the lines do not intersect each other at any point, so the pair of equations is inconsistent. Also the lines representing the graphs of the equations, meet the Y-axis at points (0, 1) and (0,3).
OR
Let XOX’ and YOY’ be the X-axis and Y-axis respectively.
Now, x – y + = 0 ⇒ x = y – 1
If y = 1, x = 0
If y = 0, x = -1
If y = 3, x = 2
Therefore,

X	0	– 1	2
Y	1	0	3

Thus, plotting the points P(0, 1), Q(- 1, 0) and R(2, 3) on the graph paper, we get the graph of x-y + 1 = 0, which is represented by PR.
Now, 3x + 2y – 12 = 0 ⇒ 2y = 12 – 3x
⇒ y = \(\frac{3(4-x)}{2}\)
If x = 4, y = 0
If x = 2, y = 3
If x = 0, y = 6
Therefore,

X	4	2	0
Y	0	3	6

Thus, plotting the points S(4, 0), R(2, 3) and T(0, 6) on the graph paper, we get the graph of 3x + 2y – 12 = 0, which is represented by ST.

The solution of the pair of equations is given by (2, 3).
Hence the coordinates of the triangle formed by these two lines and the X-axis are Q(-1, 0), R(2,3) and S(4, 0).
Area =\(\frac { 1 }{ 2 }\) × Base × Height
Now, Base = 4 – (- 1) = 5
Height = 3
Thus, Area = \(\frac { 1 }{ 2 }\) × 5 × 3 = 7.5 sq. units.

Section – E

Question 36.
Mathematics teacher of a school took her 10th standard students to show Red fort. It was a part of their Educational trip. The teacher had interest in history as well. She narrated the facts of Red fort to students. Then the teacher said in this monument one can find combination of solid figures. There are 2 pillars which are cylindrical in shape. Also 2 domes at the corners which are hemispherical 7 smaller domes at the centre. Flag hoisting ceremony on Independence Day takes place near these domes.

(i) How much cloth material will be required to cover 2 big domes each of radius 2-5 metres? (Take π = 22 / 7)
(ii) The lateral surface area of two pillars if height of the pillar is 7m and radius of the base is 1 : 4 m is:
OR
(ii) The ratio of sum of volumes of two hemispheres of radius 1 cm each to the volume of a sphere of radius 2 cm?
(iii) The volume of a hemisphere if the radius of the base is 3.5 m.
Answer:
(i) Radius of a dome, r = 2 . 5 cm
The dome is hemispherical in shape.
Then, cloth material required = 2 × Surface area of hemisphere
= 2 × 2πr²
= 4 × \(\frac { 22 }{ 7 }\) × 2.5 × 2.5
= 78.57 m²
Answer:
(ii) Height of each pillar, h = 7 m
Radius of base, r = 1.4 m
Lateral surface area or curved surface area of 2 pillars = 2 × 2πrh
= 4 × \(\frac { 22 }{ 7 }\) × 1.4 × 7
= 123.2 m²
OR
(ii) Volume of 2 hemispheres of radius 1 cm
= 2 × \(\frac { 2 }{ 3 }\) πr³ = \(\frac { 4 }{ 3 }\) π(1)³
= \(\frac { 4 }{ 3 }\) π cm³
Volume of a sphere of radius 2 cm = \(\frac { 4 }{ 3 }\) π(2)³ = \(\frac { 32 }{ 3 }\) π cm³
Then, Required ratio = \(\frac{\frac{4}{3} \pi}{\frac{32}{3} \pi}\) = \(\frac{1}{8}\) = 1 : 8

(iii) Radius of hemisphere, r = 3.5 m
Then, volume of a hemisphere,
V = \(\frac { 2 }{ 3 }\) π r³ = \(\frac { 2 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × (3.5) ³
= 89.83 m³

Question 37.
A man was standing on the top of his building from there he observe a tower at a distance from his building. He observe that top of the tower is at an angle of 30°. Then he observe same tower from the bottom of his building, the angle of elevation of the top of the tower is found to be 60°.
(i) If the height of the building is 15 m. Then find the height of the tower.
OR
If tan θ + \(\frac { 1 }{ tan θ }\) = 2, then the value of tan² θ + \(\frac{1}{\tan ^2 \theta}\) is:
(ii) what is the distance between tower and building?
(iii) If top of both building and tower are to be attach with wire then, what is the length of wire required?
Answer:
(i) In △ADE tan 30° = \(\frac{\mathrm{AE}}{\mathrm{DE}}\) = \(\frac { h }{ x }\)
= \(\frac { 1 }{ √3 }\) = \(\frac { h }{ x }\)
x = √3h ….(i)
In △ACB tan 60° = \(\frac{\mathrm{AB}}{\mathrm{CB}}\) = \(\frac {15 + h }{ x }\)
√3 = \(\frac{15+h}{\sqrt{3} h}\) [using (i)]
⇒ 3h = 15 + h
⇒ 2h = 15
h = \(\frac {15 }{ 2 }\) = 7.5 m
Height of tower = AB = BE + EA
= 15 + 7.5 = 22.5 m
OR
We have,

(ii) In △ADE, tan 30° = \(\frac{\mathrm{AE}}{\mathrm{DE}}\) = \(\frac { h }{ x }\)
= \(\frac { 1 }{ √3 }\) = \(\frac { 7 . 5 }{ x }\)
x = 7. 5 × 1.73 = 12.975 m

(iii) In △ADE sin 30° = \(\frac{\mathrm{AE}}{\mathrm{DE}}\)
\(\frac { 1 }{ 2 }\) = \(\frac { 7 . 5 }{ AD }\)
D = 7.5 × 2 = 15 m

Question 38.
On one day, a poor girl is looking for a lamp-post for completing her homework as in her area power is not there and she finds the same at some distance away from her home. After completing the homework, she is walking away from the base of a lamp-post at a speed of 1.2 m/s. The lamp post is 3.6 m above the ground and height of the girl is 90 cm (see figure).

(i) The distance of the girl from the base of the lamp post after 4 seconds:
(ii) The length of her shadow after 4 seconds is:
OR
The ratio AC : CE is:
(iii) Sides of two similar triangles are in the ratio 9:16. The ratio of corresponding area of these triangles.
Answer:
(i) Let AB denote the lamp-post and CD be the girl after walking for 4 seconds away from the lamp-post.
Now, her distance from the base of the lamp
BD = 1.2 m x 4 = 4.8 cm

(ii) △ABE ~ △CDE
\(\frac{\mathrm{BE}}{\mathrm{DE}}\) = \(\frac{\mathrm{AB}}{\mathrm{CD}}\) (Let DE = x)
⇒ \(\frac{4.8+x}{x}\) = \(\frac{3.6}{0.9}\)
⇒ 4.8 + x = 4x
⇒ x = 1.6

So, the shadow of the girl after walking for 4
OR
\(\frac{\mathrm{AE}}{\mathrm{CE}}\) = \(\frac{\mathrm{BE}}{\mathrm{DE}}\) = \(\frac{4 \cdot 8+1 \cdot 6}{1 \cdot 6}\) = \(\frac{6 \cdot 4}{1 \cdot 6}\) = 4
⇒ AE = 4CE
⇒ AC + CE = 4CE
⇒ AC = 3CE ⇒ \(\frac{\mathrm{AC}}{\mathrm{CE}}\) = \(\frac{3}{1}\)

(iii) Since ratio of the area of two similar triangles is equal to the square of their corresponding sides, Ratio of areas of similar triangles = (9)² : (16)² = 81 : 256.