CBSE Sample Papers for Class 10 Maths Standard Set 2 with Solutions

Practicing the CBSE Sample Papers for Class 10 Maths Standard Set 2 allows you to get rid of exam fear and be confident to appear for the exam.

CBSE Sample Papers for Class 10 Maths Standard Set 2 with Solutions

Section – A

Question 1.
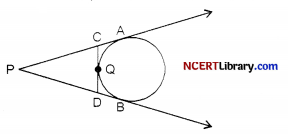
In the given figure, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then the length of AP (in cm) is:

(a) 7.5
(b) 15
(c) 10
(d) 9
Answer:
(a) 7.5
Explanation: Given, AB = 5 cm, AC = 6 cm and BC = 4 cm.
Let PB = x cm, CQ = y cm and D be the point where the tangent BC touches the circle.
So, AP = (5 + x) cm and AQ = (6 + y) cm
Also PB = BD = x cm [tangents from B]
and CQ = CD = ycm [tangents from C]
Now, 5 + x =6 + y [∵ AP = AQ]
⇒ x – y = 1 …..(i)
and x + y =4 [∵ BC = BD + CD = 4] …(ii)
Adding (i) and (ii), we get 2x = 5
⇒ x = 2.5
Thus, AP = (5 + x) cm = 7.5 cm

Question 2.
PA and PB are tangents to the circle drawn from an external point P. CD is the third tangent touching the circle at Q. If PB = 12 cm and CQ = 3 cm, then what will be the length of PC?

(a) 8 cm
(b) 9 cm
(c) 10 cm
(d) 7 cm
Answer:
(b) 9 cm
Explanation: Since, PA and PB are tangents to the circle from point P.
Therefore PA = PB …(i)
Also, CD is the tangent touching the circle at Q.
Therefore, CA = CQ and DQ = DB …(ii)
Since, tangents from external points are equal.
Now, PA = PB = 12 cm
CA =CQ = 3 cm
∵ PC = PA – CA
= 12 – 3 = 9 cm.

Question 3.
In the figure, P and Q are points on the sides AB and AC of the triangle ABC such that AP = 3.5 cm, PB = 7 cm, AQ = 3 cm and QC = 6 cm. If PQ = 4.5 cm, what is the length of BC?

(a) 13.7 cm
(b) 12.7 cm
(c) 13 cm
(d) 13.5 cm
Answer:
(d) 13.5 cm
Explanation: Given, AP = 3.5 cm, PB = 7 cm, AQ = 3 cm and QC = 6 cm.
We get, \(\frac{A P}{A B}\) = \(\frac{\mathrm{AP}}{\mathrm{AP}+\mathrm{PB}}\) = \(\frac{3.5}{10.5}\) = \(\frac{1}{3}\) , \(\frac{A Q}{A C}\) = \(\frac{\mathrm{AQ}}{\mathrm{AQ}+\mathrm{QC}}\) = \(\frac{3}{6+3}\) = \(\frac{3}{9}\) = \(\frac{1}{3}\)
⇒ \(\frac{AP}{AB}\) = \(\frac{AQ}{AC}\) = \(\frac{1}{3}\)
∴ \(\triangle \mathrm{ABC} \sim \triangle \mathrm{AQP}\) [By SS criterion]
∴ \(\frac{QP}{BC}\) = \(\frac{AQ}{AC}\) = \(\frac{AP}{AB}\)
⇒ \(\frac{4.5}{BC}\) = \(\frac{3}{9}\) [∵ Given PQ = 4.5 cm]
⇒ BC = 4.5 × 3 = 13.5
⇒ BC = 13.5 cm

Question 4.
A pendulum swings through an angle of 30° and describes an arc 6.6 cm in length then the length of pendulum is:
(a) 12.6 cm
(b) 10.6 cm
(c) 5 cm
(d) 10 cm
Answer:
(a) 12.6 cm
Explanation: Let r be the length of pendulum length of arc = 6.6 cm
∠AOB =30°

Length of an arc = \(\frac{\theta}{360^{\circ}} \times 2 \pi r\)
⇒ \(6 \cdot 6=\frac{30^{\circ}}{360^{\circ}} \times 2 \times \frac{22}{7} \times r\)
⇒ \(r=\frac{6.6 \times 360 \times 7}{2 \times 30 \times 22}\)
= \(\frac{6 \cdot 6 \times 12 \times 7}{44}\)
= \(\frac{6 \times 12 \times 7}{40}\)
r = 12.6 cm.

Question 5.
An aeroplane at an altitude of 200 m observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. What is the width of the river?
(a) 317.5 m
(b) 315.4 m
(c) 314.5 m
(d) 314.4
Answer:
(b) 315.4 m
Explanation:
Let, the width od river, AB = x m
Height of aeroplane, DC = 200 m

In △ACD, tan 45° = \(\frac { DC }{ BC }\)
⇒ 1 = \(\frac { 200 }{ AC }\)
⇒ AC = 200 m …(i)
Now, in △DBC, tan 60° = \(\frac { DC }{ BC }\)
⇒ \(\sqrt{3}=\frac{200}{B C}\)
⇒ \(\mathrm{BC}=\frac{200}{\sqrt{3}}=\frac{200 \sqrt{3}}{3}\) ….(ii)
Width of the river, AB = AC + BC
= \(200+\frac{200 \sqrt{3}}{3}\)
= \(\frac{3 \times 200+200 \sqrt{3}}{3}\)
= \(\frac{200[3+1.732]}{3}=315.4 \mathrm{~m}\)

Question 6.
Two pillars of equal height are on either side of a road, which is 100 m wide. The angles of elevation of the top of the pillars are 60° and 30° at a point on the road between the pillars. Find the hei 1 each pillar:
(a) 45.6 m
(b) 43.3 m
(c) 43 m
(d) 44 m
Answer:
(b) 43.3 m
Explanation:
Given, AB = CD
AC = 100 m

In △ABE, tan 60° = \(\frac { AB }{ AE }\)
⇒ \(\sqrt{3}=\frac{A B}{A E}\)
⇒ AB = \(\sqrt{3} \mathrm{AE}\)
In △EDC, tan 30° = \(\frac { DC }{ EC }\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac { DC }{ EC }\)
⇒ DC = \(\frac{E C}{\sqrt{3}}\) …….(ii)
Since, AB and DC are equal, from (i) and (ii), we get
\(\sqrt{3} \mathrm{AE}=\frac{\mathrm{EC}}{\sqrt{3}}\)
⇒ 3AE = EC
⇒ 3x = 100 – x [∵ AE = x]
⇒ 4x = 100 [∵ EC = 100x]
⇒ x = 25 m
So, height of pillar, AB = \(\sqrt{3} \mathrm{AE}\)
= \(\sqrt{3} \times 25\)
= \(25 \times 1.732\)
= 43.3 m
Hence, height of each pillar is 43.3 m.

Question 7.
If the mean of the following distribution is 2.6, then the value of y is:

Variable (x)	Frequency
1	4
2	5
3	y
4	1
5	2

(a) 3
(b) 8
(c) 13
(d) 24
Answer:
(b) 8
Explanation:
Mean = 2.6
Mean = \(\frac{\Sigma f x}{\Sigma f}\) = \(\frac{28+3 y}{12+y}\) ⇒ 2.6 \(\frac{28+3 y}{12+y}\)
⇒ 2.6(12 + y) = 28 + 3y ⇒ 31.2 + 2.6y = 28 + 3y
⇒ 0.4y = 3.2 ⇒ y=8.

Question 8.
A circus tent is in the shape of a cylinder and cone above it. The height of cylindrical part is 4 m and for cone its diameter is 210 m with a slant height of 40 m. What will be the total area of the canvas?
(a) 16,840 m²
(b) 10,550 m²
(c) 15,840 m²
(d) 12,040 m²
Answer:
(c) 15,840 m²
Explanation: Given,
Height of cylinder, H = 4m
Diameter of cylinder = 210 m
Radius of cylinder, r = \(\frac{210}{2}\) = 105 m

Radius of cone, r =105 m
Slant height of cone, l = 40 m.
Thus, Total canvas required = CSA of cylinder + CSA of cone
= 2πrH + πrl
= πr (2H + l)
= \(\frac{22}{7}\) × 105 (2 × 4 + 40)
= \(\frac{22}{7}\) × 105 (8 + 40)
= 22 × 15 × 48
= 15,840 m²

Question 9.
An urn contains 100 lottery tickets numbered from 1 to 100. If a ticket is selected at random, then what is the probability that it is a perfect square?
(a) 0.01
(b) 0.1
(c) 0.11
(d) 0.001
Answer:
(b) 0.1
Explanation: Perfect square = 1, 4, 9,16, 25, 36, 49, 64, 81,100
Number of perfect square =10
Total number of lottery tickets = 100
P(Number of pertect square) = \(\frac{Number of favourable event}{Total number of event}\)
= \(\frac{10}{100}\)
= 0.1

Question 10.
A bag contains 12 balls out of which ,v are black. If 6 more black balls are put in the box the probability of drawing a black ball is now double of what it was before. What is the value of x?
(a) 6
(b) 3
(c) 4
(d) 5
Answer:
(b) 3
Explanation: Given, number of balls = 12
Number of black ball = x-
More black balls added = 6
Total number of black ball = x + 6
P(black ball) = \(\frac{x}{12}\) …(i)
P(When black ball added) = \(\frac{x+6}{18}\) ….(ii)
Now, according to the question, \(2\left(\frac{x}{12}\right)\) = \(\frac{x+6}{18}\)
⇒ \(\frac{x}{6}\) = \(\frac{x+6}{18}\)
⇒ \(\frac{x}{6}\) – \(\frac{x+6}{18}\) = 0
⇒ \(\frac{x}{6}\) – \(\frac{x+6}{18}\) = 0
⇒ 2x = 6
⇒ x = 3

Question 11.
The value of cot45° + \(\left(\frac{\sec 45^{\circ}}{\sin 45^{\circ}}\right):\)
(a) 60°
(b) 90°
(c) 45°
(d) 0°
Answer:
(c) 45°
Explanation:
We know, cot 45° = 1, sec 45° = \(\sqrt{2}\), sin 45° = \(\frac{1}{\sqrt{2}}\)
On putting the values, cot 45° + \(\frac{\sec 45^{\circ}}{\sin 45^{\circ}}\) = 1 + \(\frac{\sqrt{2}}{\frac{1}{\sqrt{2}}}\)
⇒ = 1 + 2
= 3.

Alternative method
Given, sin θ = cos θ
\(\frac{sin θ}{cos θ}\) = 1
tan θ = 1
tan θ = tan 45°
∴ θ = 45°
Hence, θ

Question 12.
What is curved surface area of a hollow cylinder?
(a) 2πrh
(b) 4πr²
(c) 2πh (r + R)
(d) πrl
Answer:
(c) 2πh (r + R)
Explanation: Curved surface area of hollow cylinder is given by 2πh(r + R)
Where r = inner radius, R = Outer radius, h = height of cylinder

Question 13
If the root of the equation A x² – B x + C = 0 are -1 and 1, then which one of the following is correct?
(a) A and C are both zero
(b) A and B are both positive
(c) A and C are both negative
(d) A and C are of opposite sign
Answer:
(d) A and C are of opposite sign
Explanation:
A x² – Bx + C = 0
Since, the given roots are – 1 and 1
Sum of roots – \(\frac { (-B) }{ A }\) = \(\frac { B }{ A }\) = -1 + 1 = 0
product of roots = \(\frac { C }{ A }\) = 1 × (-1) = -1
x² – (sum of root) x + product of roots = 0
x² – \(\left(\frac{\mathrm{B}}{\mathrm{A}}\right) x\) + \(\left(\frac{\mathrm{C}}{\mathrm{A}}\right)\) = 0
But \(\frac { C }{ A }\) = Product of roots = -1
⇒ C = -A

Question 14.
What is the probability of getting a number which is neither prime nor composite in single throw of a dice?
(a) \(\frac { 1 }{ 5 }\)
(b) \(\frac { 5 }{ 6 }\)
(c) \(\frac { 1 }{ 6 }\)
(d) \(\frac { 3 }{ 5 }\)
Answer:
(c) \(\frac { 1 }{ 6 }\)
Explanation: Where a dice is throw, total probable class = 6
Favourable outcome = 1
∴ Required probability = \(\frac { 1 }{ 6 }\)

Question 15.
If one root of the quadratic equation 6 x² – x – k = 0 is \(\frac { 2 }{ 3 }\) , what is find the value of k?
(a) 1
(b) 3
(c) 2
(d) 5
Answer:
(c) 2
Explanation: Given quadratic equation is 6 x² – x – k = 0.
Put x = \(\frac { 2 }{ 3 }\) in the given equatioin
⇒ 6 \(\left(\frac{2}{3}\right)^2\) – \(\left(\frac{2}{3}\right)\) – k = 0
⇒ 6 × \(\frac { 4 }{ 9 }\) – \(\frac { 2 }{ 3 }\) – k = 0
⇒ \(\frac { 8 }{ 3 }\) – \(\frac { 2 }{ 3 }\) – k = 0
⇒ 2 – k = 0
⇒ k = 2

Question 16.
What is the LCM of 2520 and 2268 by prime factorisation ?
(a) 26820
(b) 22680
(c) 26280
(d) 22860
Answer:
(b) 22680
Explanation: We have, 2520 = 2 × 2 × 2 × 3 × 3 × 5 × 7
= 2³ × 3² × 5 × 7
2268 = 2 × 2 × 3 × 3 × 3 × 3 × 7 = 2² × 3⁴ × 7
∴ LCM (2520, 2268) = 2³ × 3⁴ × 7 × 5 = 22680.

Question 17.
If a chord of a circle of radius 14 cm makes an angle of 90° at the centre, then the area of major segment is:
(a) 560 cm²
(b) 300 cm²
(c) 160 cm²
(d) None of these
Answer:
(a) 560 cm²
Explanation:

Area of major segment = \(\frac{\theta}{360^{\circ}}\) × πr² + \(\frac{r^2 \sin \theta}{2}\)
= \(\frac{270^{\circ}}{360^{\circ}}\) × π(14)² + \(\frac{14 \times 14}{2}\) × sin 90°
= \(\frac{3 \times 14 \times 14 \pi}{4}\) + \(\frac{14 \times 14}{2}\)
= 462 + 98
= 560 cm²

Question 18.
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. If the total height of the toy is 31 cm, then the height of the cone is:
(a) 31 cm
(b) 38 cm
(c) 7cm
(d) 24 cm
Answer:
(d) 24 cm
Explanation:
Radius of sphere = Radius of cone

∴ Height of cone = Total height of toy – Radius of sphere
= (31 – 7)cm = 24 cm.

Question 19.
DIRECTION: In the question number 19 and 20, a statement of assertion (A) is followed by a statement of Reason (R).
Choose the correctoption
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A)
(b) Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A)
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Statement A (Assertion): The area enclosed by a chord and the major arc is major segment.
Statement R (Reason): If a circle is divided into three equal arcs, then each is a major arc.
Answer:
(c) Assertion is true but the Reason is false.
Explanation: For assertion, the area enclosed by a sector is proportional to the arc length of the sector.
So, A= \(\frac{\mathrm{RL}}{2}\), A = area, R= radius and L = arc length 2
Hence, the resulting enclosed area is a major segment if it is a major arc.
So assertion is true.
For reason,
We basically denote an arc as a major arc when it is greater than the semicircle and if we divide a circle into 3 arc each of it will be less than a semicircle so it is a minor arc.

Question 20.
Statement A (Assertion): A hemisphere of radius 7 cm is to be painted outside on the surface. The total cost of painting at it ? 5 per cm2 is ? 2300.
Statement R (Reason): The total surface area hemisphere is 3πr².
Answer:
(d) Assertion is false but the Reason is true.
Explanation: Total surface area of the hemisphere is
πr² + 2πr² = 3πr² = 3 × \(\frac { 22 }{ 7 }\) × 7 × 7 = 462 cm²
Cost of painting = 462 × 5 = ₹ 2310
So, assertion is false but reason is true

Section – B

Question 21.
Show that 12ⁿ cannot end with digit 0 or 5 for any natural number.
Answer:
Expressing 12 as the product of primes, we obtain
12 = 2² × 3
⇒ 12ⁿ = (2² × 3)ⁿ = 2²ⁿ × 3ⁿ
So, only prime in the factorisation of 12″ are 2 and 3 and not 5.
Hence, 12ⁿ cannot end with digit 0 or 5.

Question 22.
Is 144 a term of the A.P. : 3, 7,11, …? Justify your answer.
OR
How many integers between 200 and 500 are divisible by 8?
Answer:
Given A.P. is 3, 7,11,…
Let a_n = 144, a = 3 and d = 7 – 3 = 4
Now, a_n = 144
⇒ a + (n – 1)d – 144
⇒ 3 + (n – 1) (4) = 144
⇒ 3 + 4n – 4 = 144
⇒ 4n = 144 + 1
⇒ n = \(\frac{145}{4}\) = 36.25
∵ n is not a natural number i.e., n ∉ N.
.’. Term 144 does not exist in the given arithmetic progression.
OR
Numbers between 200 and 500 divisible by 8 are 208, 216, 224, …….496
We observe that above series is an A.P.
.’. a = 208, d = 8, a_n = 496
Now, we know that, a_n = a + (n – 1) d
⇒ 496 = 208 + (n – 1) 8
⇒ 288 = (n – 1) 8
⇒ n – 1 = 36
⇒ n =37
So, there are 37 numbers between 200 and 500, which are divisible by 8.

Question 23.
Find the values of x for which the distance between the points A(2, – 3) and B(x, 5) is 10 units.
OR
If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?
Answer:
Given points are A(2, – 3), B(x, 5) and AB = 10 units
Now, AB = 10 units
By distance formula, AB = \(\left|\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\right|\)
10 = \(\left|\sqrt{(x-2)^2+(5+3)^2}\right|\)
On squaring both sides, we get 100 =(x – 2)² + 64
⇒ (x – 2)² = 100 – 64 = 36
Taking square root on both sides, we get
x – 2 = ±6
⇒ x = 2 ± 6
.’. x = 2 + 6 = 8
and x = 2 – 6 = – 4
Hence, x = 8 and – 4.
OR
Given points are (4, k) and (1, 0), distance is 5 units.
By distance formula,
Distance = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
5 = \(\sqrt{(1-4)^2+(0-k)^2}\)
On squaring both sides,
⇒ 25 = (- 3)² + k² = 9 + k²
⇒ k² = 16
⇒ k = ± \(\sqrt{16}\) = ± 4
Hence, k = ± 4

Question 24.
If two dices are thrown simultaneously. Find the probability that the product of two numbers appearing in the two dice is less than 18.
Answer:
Total number of outcomes = 36
n(S) = 36
.’. Favourable outcomes = {(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6);
(2.1) ; (2, 2); (2, 3); (2, 4); (2, 5); (2, 6);
(3.1) ; (3, 2); (3, 3); (3, 4); (3, 5);
(4.1) ; (4, 2); (4, 3); (4,4);
(5.1) ; (5, 2); (5, 3);
(6.1) ; (6,2))
.’. Number of favourable outcomes, n(E) = 26
.’. P(product less than 18) = \(\frac{n(E)}{n(S)}\) = \(\frac{26}{36}\) = \(\frac{13}{18}\).

Question 25.
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.

Number of days	0-6	6-10	10-14	14-20	20-28	28-38	38-40
Number of students	11	10	7	4	4	3	1

Answer:

Number of days	Number of students (fi)	Class mark (xi)	fi × xi
0-6 6-10 10-14 14-20 20-28 28-38 38-40	11 10 7 4 4 3 1	3 8 12 17 24 33 39	33 80 84 68 96 99 39
	Σfi = 40		Σfi xi = 499

We know that,
Mean, \(\text { Mean, } \bar{x}=\frac{\Sigma f_i x_i}{\Sigma f_i}=\frac{499}{40}\)
\(\bar{x}=12 \cdot 475\)
.’. Mean number of days a student was absent is 12-475.

Section – C

Question 26.
A baker has 444 sweet biscuits and 276 salty biscuits. He wants to stack them in such a way that each stack has the same number and same type of biscuits and they take up the least area of the tray. What is the number of biscuits that can be placed in each stack for this purpose?
Answer:
Number of sweet biscuits in each stack = Number of salty biscuits in each stack
= H.C.F. (444, 276)
∵ 444 = 2 × 2 × 3 × 37
and 276 = 2 × 2 × 3 × 23
.’. H.C.F. (444, 276) = 2 × 2 × 3 = 12
Hence, each stack has 12 sweet and 12 salt biscuits.

Question 27.
Find the zeroes of the quadratic polynomial 5x² – 4 – 8x and verify the relationship between the zeroes and the coefficients of the polynomial.
Answer:
Given, polynomial is 5x² – 8x – 4
Here, a = 5, b = – 8 and c = – 4
5x² – 8x – 4 = 5x² – 10x + 2x – 4 = 5x(x – 2) + 2(x – 2) = (5x + 2)(x – 2)
.’. x = 2, \(\frac{-2}{5}\)
Therefore, the zero of 5x² – 8x – 4 are 2 and \(\frac{-2}{5}\)
Now, sum of Zeroes = 2 + \(\left(\frac{-2}{5}\right)\) = \(\frac{8}{5}\) = \(\frac{-b}{a}\)
product of Zeroes = 2 × \(\left(\frac{-2}{5}\right)\) = \(\frac{-9}{5}\) = \(\frac{c}{a}\)

Question 28.
Find the zeroes of the quadratic polynomial 6x² – 3 – 7x and verify the relationship between the zeroes and the coefficients of the polynomial.
Answer:
We have, 6x² – 3 – 7x = 6x² – 7x – 3
= 6x² – 9x + 2x -3
= 3x (2x – 3) + 1 (2x – 3)
= (2x – 3) (3x + 1)
Zero are: 2x – 3 = 0
or 3x + 1 = 0
.’. x = \(\frac{3}{2}\) and x = \(\frac{-1}{3}\)
Verification:
Sum of Zeroes (α + β) = \(\frac{3}{2}\) + \(\left(\frac{-1}{3}\right)\)
= \(\frac{9-2}{6}\) = \(\frac{7}{6}\)
= \(\frac{-(-7)}{6}\) = \(\frac{7}{6}\)
Product of Zeroes (αβ) = \(\frac{3}{2}\) × \(\frac{-1}{3}\) = \(\frac{-1}{2}\)
= \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)
= \(\frac{-3}{6}\) = \(\frac{-1}{2}\)
.’. Relationship holds.

Question 29.
ABCD is a trapezium with AB | | DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show that AE x FC = BF x ED.
OR
In the given figure, PA, QB and RC are perpendicular to AC such that PA = x, RC = y, QB = z, AB = a and BC = b. Prove that:
\(\frac{1}{x}\) + \(\frac{1}{y}\) = \(\frac{1}{z}\).

Answer:
Given : ABCD is a trapezium in which AB || DC || EF
To prove: AE × FC = BF × ED.
Construction : join AC which intersect EF at the point G.
Proof: In △ ADC,

EG || DC
∴ \(\frac{\mathrm{AE}}{\mathrm{ED}}\) = \(\frac{\mathrm{AG}}{\mathrm{GC}}\)
In △ ABC, GF || AB
∴ \(\frac{\mathrm{CF}}{\mathrm{BF}}\) = \(\frac{\mathrm{CG}}{\mathrm{AG}}\)
or \(\frac{\mathrm{BF}}{\mathrm{CF}}\) = \(\frac{\mathrm{AG}}{\mathrm{CG}}\) …(ii)
From equations (i) and (ii),
\(\frac{\mathrm{AE}}{\mathrm{ED}}\) = \(\frac{\mathrm{BF}}{\mathrm{CF}}\)
⇒ AE × CF = BF × ED.
OR
Given : PA, QB and RC are perpendicular to AC.
∴ PA || QB || RC

Thus, in △PAC and △QBC,
QB || PA and ∠PAC = ∠QBC = 90°
So, △QBC ~ △PAC
∴ \(\frac{\mathrm{QB}}{\mathrm{PA}}\) = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
or \(\frac{z}{x}\) = \(\frac{b}{a+b}\) ….(i)
similarly, in △RAC and △QAB, QB || RC and ∠A is common
So, △QAB ~ △RAC
∴ \(\frac{Q B}{R C}\) = \(\frac{A B}{A C}\)
or \(\frac{z}{y}\) = \(\frac{a}{(a+b)}\) ….(ii)
Adding equations (i) and (ii), we get
\(\frac{z}{y}\) + \(\frac{z}{y}\) = \(\frac{b}{(a+b)}\) + \(\frac{a}{(a+b)}\)
Or
\(z\left(\frac{1}{x}+\frac{1}{y}\right)\) = \(\frac{a+b}{a+b}\)
Or
\(\frac { 1 }{ x }\) + \(\frac { 1 }{ y }\) = \(\frac { 1 }{ z }\).

Question 30.
A jar contains green, white and yellow marbles. The probability of selecting a green marble and white marble randomly from a jar is \(\frac { 1 }{ 4 }\) and \(\frac { 1 }{ 3 }\) respectively. If this jar has 10 yellow marbles, what is the total number of marbles in the jar?
Answer:
Let, the number of green marbles = x
Number of green marbles = y
∴ Total number of marbles = x + y + 10
Now, P(selecting a green marble) = \(\frac{x}{x+y+10}\)
But it is given that,
P(green marbles) = \(\frac { 1 }{ 4 }\)
∴ \(\frac{x}{x+y+10}\) = \(\frac { 1 }{ 4 }\)
⇒ 4x = x + y + 10
⇒ 3x – y = 10 …(i)
Similarly, P(selecting a white marble) = \(\frac{y}{x+y+10}\)
∴ \(\frac{y}{x+y+10}\) = \(\frac { 1 }{ 3 }\)
⇒ 3y = x + y + 10
2y – x = 10 ……(ii)
On solving (i) and (ii), we get
y = 8 and x = 6
∴ Total no. of marbles = x + y + 10
= 6 + 8 + 10
= 24

Question 31.
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in the figure. Based on the following information, answer the following questions

(i) Find the total length of the silver wire required.
(ii) Find the area of each sector of the brooch.
(iii) Find the total cost of silver wire, if cost of silver wire is X 100 per mm.
OR
In the given figure, ABCD is a trapezium of area 24.5 sq. cm. AD || BC, ∠DAB = 90°, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region.

Answer:
Given: Diameter = 35 mm
Radius (r) = \(\frac { 35 }{ 2 }\) mm
(i) Silver wire used to make a brooch = Circumference of circle = 2πr
= 2 × \(\frac { 22 }{ 7 }\) × \(\frac { 35 }{ 2 }\) = 110 mm.
Wire used in 5 diameters = 5 × 35 mm = 175 mm
Total wire used = 110 mm + 175 mm = 285 mm

(ii) Area of circle = πr²
= \(\frac { 22 }{ 7 }\) × \(\frac { 35 }{ 2 }\) × \(\frac { 35 }{ 2 }\) mm²
= \(\frac{11 \times 5 \times 35}{2}\) mm²
Area of each sector of brooch = \(\frac{11 \times 5 \times 35}{2}\) × \(\frac { 1 }{ 10 }\) = \(\frac { 385 }{ 4 }\) mm²

(iii) Cost of silver wire = ₹ 100 × 28.5 = ₹ 2850.
OR
Given, Area of trapezium ABCD = \(\frac { 1 }{ 2 }\) × (Sum of parallel sides) x (Distance between parallel sides)
⇒ 24.5 = \(\frac { 1 }{ 2 }\) × (10 + 4) × (AB)
⇒ 24.5 = \(\frac { 1 }{ 2 }\) × (14) × (AB)
⇒ AB = \(\frac { 24.5 }{ 7 }\) = 3.5 cm
Again, AB is the radius of the quadrant of the circle.

So, area of quadrant ABE =\(\frac{\pi r^2}{4}\) = \(\frac{22}{7}\) × \(\frac{(3 \cdot 5)^2}{4}\) = 9-625 cm².
Thus, area of the shaded region = Area of trapezium ABCD – Area of quadrant ABE
= (24.5 – 9.625) cm²
= 14.875 cm².

Section – D

Question 32.
(i) Find the sum of the first 40 positive integers divisible by 6.
(ii) Determine the positive values of ‘k’ for which the equation x² + kx + 64 = 0 and x² + 8x + k = 0 will both have real roots.
Answer:
(i) The sequence of positive integers divisible by 6 can be written as : 6,12,18,24, ……………
For the given sequence a₁ = 6, a₂ = 12, a₃ = 18
Common difference d = a₂ – a₁ = a₃ – a₂ = 6
Hence, the sequence form an AP with the common difference d = 6.
The sum of first n terms, is S_n = \(\frac{n}{2}\)[2a + (n -1 )d]
Here, n = 40, a = 6, d = 6
S₄₀ = \(\frac{40}{2}\) [2 × 6 + (40 – 1)6]
= 20 [12 + 39 x 6] = 20 × 246 = 4920
Thus, the sum of the first 40 positive integers divisible by 6 is 4920.

(ii) Given equations are
x² + kx + 64 =0 ….(i)
and x² + 8 x + k =0 ….(ii)
Let D₁ and D₂ be the discriminants of equations (i) and (ii) respectively. Then,
D₁ = k² – 4 × 64 = k² – 256 and D₂ = (8)² – 4k = 64 – 4k
Both the equations will have real roots, if D₁ ≥ 0 and D₁ ≥ 0
⇒ k² – 256 ≥ 0 and 64 – 4k ≥ 0
⇒ k² – 256 ≥ 0 and 64 – 4k ≥ 0
⇒ k ≥ 16 (∵ K > 0) and k ≤ 16
⇒ k = 16
Hence, both the equations will have real roots, when k = 16.

Question 33.
Prove that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to third side.
OR
Prove that tangents to a circle from an external point are equal in length.
Answer:
Given: △ABC and a line DE intersecting AB at D and AC at E, such that
\(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)

To prove : DE || BC
Construction : Draw DE’ || BC.
Proof : ∵DE’ || BC
If a line is drawn parallel to one side of a triangle to intersect other two sides on distinct points, the other two sides are divided in the same ratio.
∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE’}}{\mathrm{E’C}}\)
and \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\) [Given]…(ii)
From equations (i) and (ii),
\(\frac{\mathrm{AE’}}{\mathrm{E’C}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
⇒ \(\frac{\mathrm{AE’}}{\mathrm{E’C}}\) + 1 = \(\frac{\mathrm{AE}}{\mathrm{EC}}\) + 1
⇒ \(\frac{A E^{\prime}+E^{\prime} C}{E^{\prime} C}\) = \(\frac{\mathrm{AE}+\mathrm{EC}}{\mathrm{EC}}\)
⇒ \(\frac{\mathrm{AC}}{\mathrm{E’C}}\) = \(\frac{\mathrm{AC}}{\mathrm{EC}}\)
⇒ \(\frac{1}{E^{\prime} \mathrm{C}}\) = \(\frac{1}{\mathrm{EC}}\)
⇒ EC = E’C
Thus, E and E’ coincide
∵ DE’ || BC
∴ DE || BC
OR
Given: PA and PB are tangents to a circle having centre O from an external point P.

To prove : PA = PB.
Construction : Join OA, OB and OP.
Proof: In △OAP and △OBP,
∠OAP = ∠OBP = 90° [Radius tangent angle]
OA = OB [Radius of the circlle]
OP = OP [common]
∴ △OAP ≅ △OBP [R.H.S. congruency rule]
⇒ AP = BP [C.P.C.T]

Question 34.
Two water taps together take 6 hours to fill a tank. If the tap with the larger diameter takes 9 hours lesser than the tap with the smaller diameter, then find the time in which each tap can separately fill the tap.
Answer:
Let the smaller tap fill the tank in x hr and the total capacity of the tank be 1 unit.
Then in 1 hr, it can fill \(\frac { 1 }{ x }\) unit.
So the larger tank takes (x – 9) hours to fill the tank.
Then in 1 hr, it can fill \(\frac { 1 }{ x – 9 }\) unit.
Together they can fill the tank in 6 hours.
Then in 1 hour, they can fill \(\frac { 1 }{ 6 }\) unit of the tank.
Thus, \(\frac { 1 }{ x }\) + \(\frac { 1 }{ x – 9 }\) = \(\frac { 1 }{ 6 }\)
⇒ \(\frac{x-9+x}{x(x-9)}\) = \(\frac { 1 }{ 6 }\)
⇒ \(\frac{2 x-9}{x(x-9)}\) = \(\frac { 1 }{ 6 }\)
⇒ 6(2x – 9) = x(x – 9)
⇒ 12x – 54 =X² – 9X
⇒ x² – 9x – 12x + 54 = 0
⇒ x² – 21x + 54 = 0
⇒ x² – 18x – 3x + 54 = 0
⇒ x(x – 18) – 3(x – 18) = 0
⇒ (x – 18)(x – 3) = 0
⇒ x = 3,18
As 9 hours less than 3 hours is – 6 which is not possible, so the smaller tap takes 18 hours to fill the tank and the larger tap takes 9 hours to do so.

Question 35.
Prove that:

\(\frac{\tan \theta}{1-\cot \theta}\) + \(\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cos θ.
OR
Amit, standing on a horizontal plane, finds a bird flying at a distance of 200 m from him at an elevation of 30°. Deepak standing on the roof of a 50 m high building, finds the angle of elevation of the same bird to be 45°. Amit and Deepak are on opposite sides of the bird. Find the distance of the bird from Deepak.
Answer:
OR

Let Amit be at C point and bird is at A point, such that ∠ACB = 30°. AB is the height of bird from point B on ground and deepak is at D point, DE is the building of height 50m.
Now, in right △ABC, we have
sin 30° = \(\frac{\mathrm{P}}{\mathrm{H}}\) = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac { 1 }{ 2 }\) = \(\frac{\mathrm{AB}}{\mathrm{200}}\)
⇒ AB = 100 m

In right △AFD, we have
sin 45° = \(\frac{\mathrm{AF}}{\mathrm{AD}}\)
⇒ \(\frac{1}{\sqrt{2}}\) = \(\frac{50}{\mathrm{AD}}\)
⇒ AD = \(50 \sqrt{2}\) m
Hence, the distance of bird from Deepak is \(50 \sqrt{2}\) m

Section – E

Question 36.
A student of class X was enjoying evening tea with her friend in the balcony. Her friend Jiya was discussing the concept of arrangement of iron bars used in the construction of her balcony. She told Jiya that frame of iron bars is farmed in a straight line manner. Such a prototype is shown below. Here another diagram is showing arrangement of rods fixed in balcony then answer the following question based on the figure.

(i) If the coordinates of points are C (5, 6) and D (10, 11). Find the distance between points C and D.

(ii) Refer to the point E, U and F. Point U divides the line segment joining the points E (- 4, 3) and F(9,8) such as \(\frac{\mathrm{EU}}{\mathrm{UF}}\) = \(\frac{\mathrm{k}}{\mathrm{l}}\). If U lies on the line 3x + y + 2 = 0, find the value of k.
OR
Refer to the points AJ, if the coordinates are A(- 2, – 2) and J (3, – 9) respectively. Find coordinates of U such that AU = \(\frac { 3 }{ 4 }\) AJ.

(iii) Refer to the point E (-4, 3) and F (9, 8).
Find the coordinates of G, such that \(\frac{\mathrm{EG}}{\mathrm{GF}}\) = \(\frac { 4 }{ 3 }\).
Answer:
(i) The distance formula for given coordinates C(5, 6) and D(10,11)
D = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
= \(\sqrt{(10-5)^2+(11-6)^2}\)
= \(\sqrt{(5)^2+(5)^2}\)
= \(\sqrt{25+25}\)
= \(\sqrt{50}\) = 5\(\sqrt{2}\)
= 5 × 1.414
= 7.070 units

(ii) Given that U divides the line segment joining E(-4, 3) and F(9,8) in the ratio k : l.
So the coordinates of U are \(\left(\frac{9 k-4}{k+1}, \frac{8 k+3}{k+1}\right)\)

U \(\left(\frac{9 k-4}{k+1}, \frac{8 k+3}{k+1}\right)\) lies on the segment 3 x + y + 2 = 0
⇒ \(3\left(\frac{9 k-4}{k+1}\right)\) + \(\frac{8 k+3}{k+1}\) + 2 = 0
⇒ 27k – 12 + 8k + 3 = -2(k + 1)
⇒ 27k – 12 + 8k + 3 = -2k -2
⇒ 37k = 7
⇒ k = \(\frac { 7 }{ 37 }\)
OR
We have AU = \(\frac { 3 }{ 4 }\) AJ

\(\frac{\mathrm{AU}}{\mathrm{AJ}-\mathrm{AU}}\) = \(\frac{3}{4-3}\)
⇒ \(\frac{\mathrm{AU}}{\mathrm{JU}}\) = \(\frac{3}{1}\)
∴ U (x,y) is given by
x = \(\frac{3(3)+1(-2)}{3+1}\) = \(\frac{9-2}{4}\) = \(\frac{7}{4}\)
y = \(\frac{3(-9)+1(-2)}{3+1}\) = \(\frac{-27 -2}{4}\) = \(\frac{-29}{4}\)
Thus, coordinates of U(x,y) are x \(\left(\frac{7}{4}, \frac{-29}{4}\right)\).

(iii) Given that

\(\frac{\mathrm{EG}}{\mathrm{GF}}\) = \(\frac{4}{3}\) or EG : GF = 4 : 3
Let the coordinates of G be (x,y)
Then, x = \(\frac{4 \times 9+3(-4)}{4+3}\) = \(\frac{36-12}{7}\) = \(\frac{24}{7}\)
y = \(\frac{4(8)+3(3)}{4+3}\) = \(\frac{32+9}{7}\) = \(\frac{41}{7}\)
∴ The coordinates of G are \(\left(\frac{24}{7}, \frac{41}{7}\right)\)

Question 37.
A practical application of the trigonometry functions is to find the length that you cannot measure. Very frequently, angles of depression and elevation are used in these type of problems. Angle of depression is the angle measured from the horizon or horizontal Y line down.

A boy is riding in a hot air bolloon. When he is at the point A, he spotted a car parked in the ground at an angle of depression of 45°. After some time, his balloon x’ rises to some of height and reached at A’. Now for the some point, the angle of depression changes to 60°.
Now, answer the following questions :
(i) What is the value of ZAQP?
(ii) If the height of air-balloon at point A is ‘h’m from the ground. Find the distance of the point ‘A’ from the parked car? (in terms of h)
(iii) If the balloon rises to a height of 12 m, find the height of the balloon at the initial point i.e., height ‘h’ ?
OR
What is the final height of balloon after a lapse of time at point A?
Answer:
(i) Since, line AX || QP and QA is a transversal.
⇒ ∠XAQ = ∠AQP = 45° (Alternate pair of angles)

(ii) In △APQ,
sin 45° = \(\frac{\mathrm{AP}}{\mathrm{AQ}}\)
⇒ \(\frac{1}{\sqrt{2}}\) = \(\frac{h}{\mathrm{AQ}}\)
⇒ AQ = \(\sqrt{2} h\)

(iii) In △APQ,
tan 45° = \(\frac{\mathrm{AP}}{\mathrm{PQ}}\)
⇒ AP = PQ = h ….(i)
Now, in △A’PQ, tan 60° = \(\frac{\mathrm{A’P}}{\mathrm{PQ}}\)
⇒ \(\sqrt{3} h-h=12\)
⇒ \(\sqrt{3} h-h=12\)
⇒ h = \(\frac{12}{0.73}\) = 16.43 m
OR
As, h = 16.43
Then, A’P = 12 + 16.43
= 28.43 m

Question 38.
Consider a circular field of radius ‘r’ m Seema is at some distance from the boundary of the circular field as shown is the figure.

The distance of Seema from the boundary of the field is 25 m. The point at which Seema is standing, a tangent is drawn to the circular field which is of length 35 m.
Now, answer the following questions :
(i) What is the radius of the circular field?
OR
If ∠BCA = 30°, then what is the value of ∠BAC?
(ii) What is the distance of Seema from the centre of the field?
(iii) What is the area of a circle?
Answer:
(i) Since, BC is a tangent to a circle
∴ ∠CBA =90°
By applying Pythagoras theorem,
In △ABC,
AC² = AB² + BC²
(r + 25)² = r² + 35²
⇒ r² + 625 + 50r = r² + 1225
⇒ 50r = 600
⇒ r = 12 cm
OR
Since, △ABC is a right angled triangle at B. As tangent to a circle is perpendicular to the radius at point of contact at point of contant
∴ 90° + 30° + ∠BAC = 180°
⇒ ∠BAC = 180° – 120° = 60°

(ii) Distance from the centre = r + 25 = 12 + 25 = 37 m

(iii) πr² = π × (12)²
= 1447 π m²