CBSE Sample Papers for Class 10 Maths Basic Set 5 with Solutions

Practicing the CBSE Sample Papers for Class 10 Maths Basic Set 5 allows you to get rid of exam fear and be confident to appear for the exam.

CBSE Sample Papers for Class 10 Maths Basic Set 5 with Solutions

Time Allowed : 3 hours
Maximum Marks : 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D, and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answer-II (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each) with sub-parts of the values of 1,1 and 2 marks each respectively.
7. All Questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take n = \(\frac{22}{7}\) wherever required if not stated.

Section – A
(Section A consists of 20 Questions of 1 marks each.)

Question 1.
The (HCF × LCM) for the numbers 50 and 20 is : [1]
(A) 1000
(B) 50
(C) 100
(D) 500
Answer:
(A) 1000

Explanation:
We know that HCF × LCM = Product of two numbers
⇒ HCF × LCM = 20 × 50
∴ HCF × LCM = 1000

Question 2.
The number of polynomials having zeroes as -2 and 5 is : [1]
(A) 1
(B) 2
(C) 3
(D) more than 3
Answer:
(D) more than 3

Explanation :
We know that if we divide or multiply a polynomial by any constant (real number), then the zeroes of polynomial remains same.
Here, α = -2
and ß = +5
∴ α + ß = -2 + 5 = 3
and αß = -2 × 5 = -10
So, required polynomial is
x² – (a + b)x + ab = x² – 3x – 10
If we multiply this polynomial by any real number,
let 5 and 2, we get 5x² – 15x – 50 and 2x² – 6x – 20
which are different polynomials but having same zeroes -2 and 5.
So, we can obtain so many (infinite polynomials) from two given zeroes.

Question 3.
The common difference of the A.E :\(\frac{1}{p}, \frac{1-p}{p}, \frac{1-2 p}{p}\) is : [1]
(A) p
(B) -p
(C) – 1
(D) 1
Answer:
(C) – 1

Explanation : Common difference,
d = \(\frac{1-p}{p}-\frac{1}{p}\)
= \(\frac{1-p-1}{p}\)
= \(\frac{-p}{p}\)
= -1

Question 4.
If in two triangles DEF and PQR. ∠D = ∠Q and ∠R = ∠E, then which of the following is not true? [1]
(A) \(\frac{E F}{P R}=\frac{D F}{P Q}\)
(B) \(\frac{D E}{P Q}=\frac{F E}{R P}\)
(C) \(\frac{D E}{Q R}=\frac{D F}{P Q}\)
(D) \(\frac{E F}{R P}=\frac{D E}{Q R}\)
Answer:
(B) \(\frac{D E}{P Q}=\frac{F E}{R P}\)

Explanation :
In ∆DEF and ∆PQR, ∠D = ∠Q and ∠R = ∠E.
By AA similarity, we get ∆DEF ~ ∆QRP.
Hence, \(\frac{D E}{Q R}=\frac{E F}{R P}=\frac{D F}{P Q}\)

Question 5.
If the product of the roots of equation kx² + 2x + 3k = 0 is equal to their sum then the value of k is: [1]
(A) \(\frac{-1}{3}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{-2}{3}\)
Answer:
(D) \(\frac{-2}{3}\)

Explanation:
Sum of roots = –\(\frac{2}{k}\)
and product of roots = \(\frac{c}{a}\) = \(\frac{3k}{k}\) = 3
∵ product of roots = sum of roots
⇒ –\(\frac{2}{k}\) = 3
⇒ k = –\(\frac{2}{3}\)

Question 6.
LCM of smallest prime and smallest composite number is : [1]
(A) 1
(B) 2
(C) 3
(D) 4
Answer:
(D) 4

Explanation:
We know that,
Smallest prime number = 2
Smallest composite number = 4
LCM (2, 4) = 4

Question 7.
If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then the length of each tangent is equal to : [1]

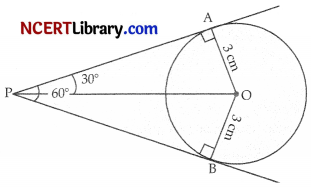
(A) \(\frac{3}{2}\)\(\sqrt{3}\) cm
(B) 6 cm
(C) 3 cm
(D) 3\(\sqrt{3}\) cm
Answer:
(D) 3\(\sqrt{3}\) cm

Explanation :
Let, OA and PA be the radius and the tangent respectively at contact point A of a circle of radius
OA = 3 cm
∴ ∠PAO = 90°
In right angled ΔPOA,
tan 30° = \(\frac{\text { Perpendicular }}{\text { Base }}\) = \(\frac{OA}{PA}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{3}{PA}\)
⇒ PA = 3\(\sqrt{3}\)

Question 8.
9 cosec² A – 9 cot² A = [1]
(A) 1
(B) 9
(C) 8
(D) 0
Answer:
(B) 9

Explanation :
9 cosec² A – 9 cot² A = 9 (cosec² A – cot² A)
= 9 × 1 = 9
[∵ cosec² A – cot²A = 1]

Question 9.
Which of the following numbers can form the sides of a right angle triangle? [1]
(A) 13 cm, 27 cm, 15 cm
(B) 4 cm, 5 cm, 9 cm
(C) 10 cm, 6 cm, 8 cm
(D) 2cm, 9 cm, 17 cm
Answer:
(C) 10 cm, 6 cm, 8 cm

Explanation:
Here, 27² ≠ 13² + 15²
9² ≠ 4² + 5²
10² = 6² + 8²
17² ≠ 2² + 9²

Question 10.
In the figure of ∆ABC, the points D and E are on the sides CA, CB respectively such that DE || AB, AD = 2x, DC = x + 3, BE = 2x – 1 and CE = x. Then, x is: [1]

(A) \(\frac{3}{5}\)
(B) \(\frac{2}{5}\)
(C) \(\frac{1}{5}\)
(D) \(\frac{4}{5}\)
Answer:
(A) \(\frac{3}{5}\)

Explanation :
\(\frac{C D}{C A}=\frac{C E}{B E}\)
or, \(\frac{x+3}{2x}=\frac{x}{2x-1}\)
or, 5x = 3 or, x = \(\frac{3}{5}\)

Detailed Answer :
In ABC, DE|| AB (Given)
Then, \(\frac{C D}{C A}=\frac{C E}{B E}\) [∵ BPT]
or, \(\frac{C D}{C D + AD}=\frac{C E}{C E + B E}\)
or, \(\frac{x+3}{x+3+2x}=\frac{x}{x+2x-1}\)
or, \(\frac{x+3}{3x+3}=\frac{x}{3x-1}\)
or, (x + 3)(3x – 1) = x(3x + 3)
or, 3x² – x + 9x – 3 = 3x² + 3x
or, 8x – 3 = 3x
or, 8x – 3x = 3
or, 5x = 3
∴ x = \(\frac{3}{5}\)

Question 11.
If the perimeter and the area of a circle are numerically equal, then the radius of the circle is : [1]
(A) 2 units
(B) π units
(C) 4 units
(D) 7 units
Answer:
(A) 2 units

Explanation :
Let the radius of the circle be r.
Circumference of circle = 2πr
Area of circle = πr²
Given that, the circumference of the circle and the area of the circle are equal.
This implies,
2πr = πr²
r = 2
Therefore, the radius of the circle is 2 units.

Question 12.
Volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is : [1]
(A) 3 : 4
(B) 4 : 3
(C) 9 : 16
(D) 16 : 9
Answer:
(C) 9 : 16

Explanation :

Question 13.
The diameter of a car wheel is 42 cm. The number of complete revolutions it will make in moving 132 km is [1]
(A) 104
(B) 10
(C) 106
(D) 103
Answer:
(B) 10

Explanation:
Diameter of wheel = 42 cm
Radius of the wheel = \(\frac{42}{2}\)
= 21 cm
Distance in 1 revolution = Circumference of the wheel
= 2πr
= 2 × \(\frac{22}{7}\) × 21
= 132 cm
Total distance covered by the wheel = 132 km = 132 × 100000 cm = 13200000 cm
Number of revolutions \(\frac{\text { Total distance covered by wheel }}{\text { Distance covered in 1 revolution }}\)
= \(\frac{13200000}{132}\) = 100000 = 10⁵

Question 14.
Consider the following frequency distribution : [1]

Class	0-5	6-11	12-17	18-23	24-29
Frequency	13	10	15	8	11

the upper limit of the median class is :
(A) 7
(B) 17.5
(C) 18
(D) 18.5
Answer:
(B) 17.5

Explanation :

Class	Frequency	Cumulative frequency
0.5-5.5	13	13
5.5-11.5	10	23
11.5-17.5	15	38
17.5-23.5	8	46
23.5-29.5	11	57

The median of 57 (odd) observations
= \(\frac{(57+1)}{2}\)
= \(\frac{58}{2}\) = 29th term
29th term lies in class 11.5-17.5.
So, upper limit is 17.5. 1

Question 15.
Two different coins are tossed simultaneously. The probability of getting at least one head is : [1]
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{8}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{7}{8}\)
Answer:
(C) \(\frac{3}{4}\)

Explanation :
S = {HH, HT, TH, TT}
A = {HH, HT, TH}
n(S) = 4
n(A) = 3
∴ P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{3}{4}\)

Question 16.
If cos (α + ß) = 0, then α + ß is equal to [1]
(A) 45°
(B) 30°
(C) 90°
(D) 60°
Answer:
(C) 90°

Explanation :
cos (α + ß) = 0
cos(α + ß) = cos 90°
α + ß = 90°

Question 17.
If cot θ = \(\frac{1}{\sqrt{3}}\), the value of sec² θ + cosec² θ is [1]
(A) 1
(B) \(\frac{40}{9}\)
(C) \(\frac{38}{9}\)
(D) 5\(\frac{1}{3}\)
Answer:
(D) 5\(\frac{1}{3}\)

Explanation:
It is given that
cot θ = \(\frac{1}{\sqrt{3}}\) = cot 60°
⇒ θ = 60°
Substituting the value of θ
sec² θ + cosec² θ = sec² 60° + cosec² 60°
= (2)² + (\(\frac{1}{\sqrt{3}}\))²
= 4 + \(\frac{4}{3}\)
= \(\frac{16}{3}\)
= \(5 \frac{1}{3}\)

Question 18.
The ratio in which the point (-3, k) divides the line segment joining the points (-5, -4) and (-2,3) is: [1]
(A) 1:3
(B) 2:1
(C) 2:3
(D) 1:2
Answer:
(B) 2:1

Explanation:

Let the ratio in which P divides AB be n : 1.
Considering x co-ordinate for section formula
-3 = \(\frac{(-2)n+1(-5)}{n+1}\)
or, -3(n + 1) = – 2n – 5
or, -3n -3 = – 2n – 5
5 – 3 = 3n – 2n
2 = n
∴ Ratio, \(\frac{n}{1}\) = \(\frac{2}{1}\) or 2 : 1 ½

Directions for Question 19 and 20: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true but (R) is NOT the correct explanation of (A).
(C) (A) is true but (R) is false.
(D) (A) is false and (R) is true.

Question 19.
Assertion (A): (7 × 13 × 11) + 11 and (7 × 6 × 5 × 4 × 3 × 2 × 1) + 3 have exactly composite numbers.
Reason (R): (3 × 12 × 101) + 4 is not a composite number. [1]
Answer:
(C) (A) is true but (R) is false.

Explanation:
Consider the assertion,
Since (7 × 13 × 11) + 11 = 11 × (7 × 13 + 1)
= 11 × (91 + 1)
=11 × 92
⇒ 11 × 2 × 2 × 23
and (7 × 6 × 5 × 4 × 3 × 2 × 1) + 3
= 3 (7 × 6 × 5 × 4 × 2 × 1 + 1)
= 3 × (1681) ⇒ 3 × 41 × 41
Given numbers have more than two prime factors.
So, both the numbers are composite.
Hence, assertion is correct.
Now, let us consider the reason
3 × 12 × 101 + 4 = 4(3 × 3 × 101 + 1)
= 4(909 + 1)
= 4(910)
= 2 × 2 × 2 × 5 × 7 × 13
= a composite number
[∵ Product of more than two prime factors]
Hence, reason is not correct.
Thus, assertion is correct but reason is incorrect.

Question 20.
Assertion (A): The ordinate of a point A on y-axis is 5 and B has coordinates (-3,1). Then the length of AB is 5 units.
Reason (R): The point A(2, 7) lies on the perpendicular bisector of line segment joining the points P(6, 5) and Q(0, -4). [1]
Answer:
(C) (A) is true but (R) is false.

Explanation:
In case of assertion:
Here, A → (0 , 5) and B → (- 3 , 1)
AB = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\)
= \(\sqrt{(-3-0)^2 + (1-5)^2}\)
= \(\sqrt{9 + 16}\)
= \(\sqrt{25}\)
= 5 units
∴ Assertion is correct.
In case of reason:
If A (2, 7) lies on perpendicular bisector of P (6, 5) and Q (0, -4), then
AP = AQ
∴ By using Distance Formula,
AP = \(\sqrt{(6-2)^2 + (5-7)^2}\)
= \(\sqrt{4^2 + -2^2}\)
= \(\sqrt{20}\)
And AQ = \(\sqrt{(0-2)^2 + (-4-7)^2}\)
= \(\sqrt{(-2)^2 + (-11)^2}\)
= \(\sqrt{125}\)
As, AP ≠ AQ
Therefore, A does not lie on the perpendicular bisector of PQ.
∴ Reason is incorrect.
Hence, assertion is correct but reason is incorrect.

Section – B
Section B consists of 5 Questions of 2 marks each.

Question 21.
If m and n are the zeroes of the polynomial 3x² + 11x – 4, find the value of \(\frac{m}{n}\) + \(\frac{n}{m}\)
OR
Find whether the lines represented by 2x + y = 3 and 4x + 2y = 6 are parallel, coincident or intersecting. [2]
Answer:
Let p(x) = 3x² + 11x – 4 = 0
3x² + 12x – x – 4 = 0
3x(x + 4) – 1(x + 4) = 0
(3x – 1) (x + 4) = 0
So, zeroes are, x = \(\frac{1}{3}\)
⇒ m = \(\frac{1}{3}\)
and x = – 4 ⇒ n = – 4
Now, \(\frac{m}{n}\) + \(\frac{n}{m}\) = \(\frac{\frac{1}{3}}{-4}\) + \(\frac{-4}{\frac{1}{3}}\)
= \(\frac{1}{-12}\) – 12
= \(\frac{-145}{12}\)
Alternative Solution :
Let p(x) = 3x² + 11x – 4 = 0
Given, m and n are zeroes of p(x).
Then, m + n = sum of zeroes = – \(\frac{11}{3}\)
m × n = product of zeroes
= –\(\frac{4}{3}\)
Now,

OR
OR
Here, a₁ = 2, b₁ = 1, c₁ = – 3
and a₂ = 4, b₂ = 2, c₂ = – 6
If \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\),
then the lines are coincident.
Clearly, \(\frac{2}{4}=\frac{1}{2}=\frac{3}{6}\)
Hence, lines are coincident.

Question 22.
In the given figure, PQ and PR are tangents to the circle with centre O such that ∠QPR = 45°, then find ∠QOR. [2]

Answer:
Since, OR ⊥ PR and OQ ⊥ PQ
(angle between radius and tangent)
∴ ∠QPR = 90° = ∠OQP
In quadrilateral PQOR,
∠PQO + ∠QOR + ∠ORP + ∠RPQ = 360°
⇒ 90° + ∠QOR + 90° + 45° = 360°
⇒ ∠QOR = 360° – 225° = 135°

Question 23.
ABC is a triangle. A circle touches sides AB and AC produced and side BC at X, Y and Z respectively. Show that AX = \(\frac{1}{2}\) perimeter of ∆ABC. [2]
Answer:
Perimeter of DABC(P) = AB + AC + BC
= (AX – BX) + (AY – CY) + (BZ + ZC)
= AX + AY – BX + BZ + ZC – CY
The tangents of a circle, from an external point are equal.

or, From point B → BX = BZ
From A → AX = AY
and from point C → CZ = CY
∴ P = AX + AY = 2AX
or AX = \(\frac{1}{2}\) Perimeter of DABC.

Question 24.
Prove that \(\frac{\cos ^3 \theta+\sin ^3 \theta}{\cos \theta+\sin \theta}+\frac{\cos ^3 \theta-\sin ^3 \theta}{\cos \theta-\sin \theta}=2\) [2]
Answer:

Hence Proved.

Question 25.
What is the volume of a right circular cylinder of base radius 7 cm and height 10 cm ? (Use π = \(\frac{22}{7}\))
OR
The rain water from 22 m × 20 m roof drains into cylindrical vessel of diameter 2 m and height 3.5 m. If the rain water collected from the roof fills (\(\frac{4}{5}\)) of cylindrical vessel then find the rainfall in cm. [2]
Answer:
Here, r = 7 cm, h = 10 cm
Volume of cylinder = πr²h
= \(\frac{22}{7}\) × (7)² × 10
= 1540 cm³
OR
Volume of water collected in cylindrical vessel
= \(\frac{4}{5}\) × π × (1)² × (\(\frac{7}{2}\)) m³
= \(\frac{44}{5}\) m³

Let the rainfall is h m.
Volume of rain water from roof = 22 × 20 × h m³
or, 22 × 20 × h = \(\frac{44}{5}\)
or, h = \(\frac{44}{5}\) × \(\frac{1}{22×20}\) = \(\frac{1}{50}\) m
= \(\frac{1}{50}\) × 100 = 2 m

Section – C
Section C consists of 6 Questions of 3 marks each.

Question 26.
144 cartons of Coke cans and 90 cartons of Pepsi cans are to be stacked in a canteen. If each stack is of the same height and if it contain equal cartons of the same drink, what would be the greatest number of cartons each stock would have ? [3]
Answer:
Since, the greatest number of cartons is the HCF of
144 and 90. 1
144 = 2⁴ × 3²
90 = 2 × 3² × 5
Therefore, HCF= 2 × 3² = 18
Thus the greatest number of cartons = 18.

Question 27.
In an A.E if sum of its first n terms is 3n² + 5n and its k^th term is 164, find the value of k.
OR
The sum of ages (in years) of a son and his father is 35 years and product of their ages is 150 years, find their ages. [3]
Answer:
Here, S_n = 3n² + 5n
⇒ S₁ = 3.1² + 5.1 = 8 = a₁
S₂ = 3.2² + 5.2
= 22 = a₁ + a₂
a₂ = 22 – 8 = 14 ⇒ d = 6
a_k = 164
⇒ 8 + (k – 1)6 = 164
⇒ k = 27
OR
Let the age of father be x years.
and age of son be y years.
∴ x + y = 35 and xy = 150
or y = 35 – x
Putting the value of y in xy = 150
x(35 – x) = 150
⇒ x² – 35x + 150 = 0
⇒ (x – 30)(x – 5) = 0
⇒ x = 30 or x = 5 (rejected)
⇒ y = 5
Hence, the age of father = 30 years and the age of son = 5 years.

Question 28.
In a certain A.E 32^th term is twice the 12^th term. Prove that 70^th term is twice the 31^st term. [3]
Answer:
Let the 1^st term be a and common difference be d.
According to the question, a₃₂ = 2a₁₂
∴ a + 31d = 2(a + 11d)
a + 31d = 2a + 22d
a = 9d
Again, a₇₀ = a + 69d
= 9d + 69d = 78d
a₃₁ = a + 30d
= 9d + 30d = 39d
Hence, a₇₀ = 2a₃₁
Hence Proved.

Question 29.
The angle of elevation of the top B of a tower AB from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Find the height of the tower AB and the distance XB. [3]
Answer:
In ∆YCB, we have

tan 45° = \(\frac{B C}{Y C}\)
1 = \(\frac{x}{Y C}\)
YC = x m
⇒ XA = x m
In ∆XAB,
tan 60° = \(\frac{A B}{X A}\)
\(\sqrt{3}\) = \(\frac{x+40}{x}\)
\(\sqrt{3}\)x = x + 40
x \(\sqrt{3}\) – x = 40
x = \(\frac{40}{\sqrt{3}-1} \times \frac{\sqrt{3}+1}{\sqrt{3}+1}\)
= 20(\(\sqrt{3}\)+1)
= (20\(\sqrt{3}\)+1) m
∴ Height of the tower AB = x+ 40
= 20 \(\sqrt{3}\) + 20 + 40
= 20 \(\sqrt{3}\) + 60
= 20(\(\sqrt{3}\) + 3) m
In ∆XAB,
sin 60° = \(\frac{AB}{BX }\)
\(\frac{\sqrt{3}}{2}\) = \(\frac{AB}{BX}\)
BX = \(\frac{20(\sqrt{3}+3)2}{\sqrt{3}}\)
\(=40(\sqrt{3}+1)\)
= 40 × 2.73 m
= 109.20 m

Question 30.
The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and intersecting the larger circle at P on producing. Find the length of AE. [3]
Answer:

∠APB = 90° [angle in semi-circle]
and ∠ODB = 90° [radius is perpendicular to tangent]
∠B = ∠B
∆ABP ~ ∆OBD (AA Similarity)
⇒ \(\frac{AB}{OB}=\frac{AP}{OD}\)
⇒ \(\frac{26}{13}=\frac{AP}{8}\)
Hence, AP = 16 cm.

Question 31.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angle of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between these points. [3]
OR
Prove that : \(\frac{{cosec}^2 \theta}{{cosec} \theta-1}-\frac{{cosec}^2 \theta}{{cosec} \theta+1}=2 \sec ^2 \theta\) [3]
Answer:

In ∆DCA, \(\frac{DC}{CA}= tan 60°\)
⇒ \(\frac{15}{x}=\sqrt{3}\)
⇒ x = \(\frac{15}{\sqrt{3}}\)
⇒ x = 5\(\sqrt{3}\)

In ∆DCB, \(\frac{D C}{C B}=\tan 45^{\circ}=\frac{15}{x+y}=1\)
⇒ x + y = 15
⇒ 5 \(\sqrt{3}\) + y = 15
⇒ y = 15 – 5 \(\sqrt{3}\)
= 5(3 – \(\sqrt{3}\)) m
Hence, the distance between the points
= 5(3 – \(\sqrt{3}\)) m
OR

Section – D
Section D consists of 4 Questions of 5 marks each.

Question 32.
If 2 is subtracted from the numerator and 1 is added to the denominator, a fraction becomes \(\frac{1}{2}\), but when 4 is added to the numerator and 3 is subtracted from the denominator, it becomes \(\frac{3}{2}\). Find the fraction. [5]
OR
Find the values of k for which the equation (3k + 1)x² + 2(k + 1)x + 1 has equal roots. Also find the roots.
Answer:
Let the fraction be \(\frac{x}{y}\).
According to the problem,
\(\frac{x-2}{y+1}=\frac{1}{2}\)
or, 2x – 4 = y + 1
or, 2x – y = 5 …(i)
Also, \(\frac{x+4}{y-3}=\frac{3}{2}\)
⇒ 2x + 8 = 3y – 9
⇒ 2x – 3y = -17 …(ii)
Subtracting eqn. (ii) from eqn. (i),
2y = 22
∴ y = 11
Substituting this value of y in eqn. (i),
2x – 11 = 5
∴ x = 8
Hence, fraction = \(\frac{8}{11}\)
OR
Since, the given equation has equal roots,
D = b² – 4ac = 0 1
Here, a = (3k + 1), b = 2(k + 1) and c = 1
[2(k + 1)]² – 4(3k + 1)(1) = 0
⇒ 4(k² + 2k + 1) – (12k + 4) = 0
⇒ 4k² + 8k + 4 – 12k – 4 = 0
4k² – 4k = 0
∴ 4k(k – 1) = 0
k = 0, 1
Put k = 0, in the given equation,
x² + 2x + 1 = 0
⇒ (x + 1)² = 0
⇒ x = -1
Again, put k = 1, in the given equation,
4x² + 4x + 1 = 0
(2x + 1)² = 0
⇒ x = –\(\frac{1}{2}\)
Hence, roots = -1,-\(\frac{1}{2}\)

Question 33.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O.
Show that \(\frac{A O}{B O}=\frac{C O}{D O}\). [5]
Answer:
Proof : In ∆AOB and ∆COD,
AB || CD

∴ ∠OAB = ∠DCO
and ∠OBA = ∠ODC
(Alternate angles)
∴ ∆AOB ~ ∆COD (AA similarity)
∴ \(\frac{A O}{C O}=\frac{B O}{D O}\)
(Corresponding sides of similar triangles)
Hence, \(\frac{A O}{B O}=\frac{C O}{D O}\).

Question 34.
A solid cylinder of diameter 12 cm and height 15 cm is melted and recast into toys in the shape of a cone of radius 3 cm and height 9 cm. Find the number of toys so formed. [5]
Answer:
Given, height of cylinder = 15 cm
and its diameter = 12 cm
∴ radius = 6 cm
radius of cone = 3 cm
and height = 9 cm
Let the number of toys recast be n.
∴ Volume of n conical toys = Volume of cylinder

n × \(\frac{1}{2}\) π × 3 × 3 × 9 = π × 6 × 6 × 15
n = \(\frac{6×6×15}{3×9}\)
n = 20
Hence the number of toys = 20.

Question 35.
On annual day of a school, 400 students participated in the function. Frequency distribution showing their ages is as shown in the following table : [5]

Age (in years)	05-07	07-09	09-11	11-13	13-15	15-17	17-19
Number of students	70	120	32	100	45	28	5

Find mean and median of the above data.
OR
(i) Find the mean of the following distribution :

Class interval	0-6	6-12	12-18	18-24	24-30
Frequency	5	4	1	6	4

(ii) Two dice are rolled simultaneously. Find the probability that the sum of numbers appearing is 10.
Answer:

Let a = Assumed mean = 12
Mean, \(\bar{x}=a +\frac{Σf_iu_i}{Σf_i}×h\)
Mean = 12 + \(\frac{-366}{400}×2\) = 12 – \(\frac{-183}{100}\)
= 12 – 1 8. 3 = 10.17
For Median class, \(\frac{N}{2}\)
= \(\frac{400}{2}\) = 200 (09 – 11 is the median class)
\(\text { Median }=l+(\left[\frac{\frac{N}{2}-c.f.}{f}\right]) ×h\)
∴ Median = 9 + \(\frac{200-190}{32}\) × 2
= 9 \(\frac{10}{32}\) × 2
= 9 + 0.625 = 9.625

OR

C.I.	xi	fi	xifi
0-6	3	5	15
6-12	9	4	36
12-18	15	1	15
18-24	21	6	126
24-30	27	4	108
Total		Σfi=20	Σxifi=300

Mean = \(\frac{Σf_ix_i}{Σf_i}\)
= \(\frac{300}{20}\)
= 15

(ii) When two dice are thrown, no. of all possible outcomes = 6 × 6 = 36
Since, sum of both faces should be 10, they are,
{(4, 6), (6, 4), (5, 5)}
∴ No. of favourable outcomes = 3
∴ P(E) = \(\frac{3}{36}\) = \(\frac{1}{12}\)

Section – E
Case study based questions are compulsory.

Question 36.
The diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of the sun room are square clear glass panels. The roof is B made using,

• Four clear glass panels, trapezium in shape, all of the same size
• One tinted glass panel, half a regular octagon in shape

I. Refer to Top View, find the mid-point of the segment joining the points J(6,17) and I(9,16).
II. Refer to the front View, find the distance of point P from the y-axis:
III. Refer to the front view, find the distance of points A and S.
Refer to front view, find the co-ordinates of the point which divides the line segment joining the points A and B in the ratio 1: 3 internally.
Answer:
I. Mid-point of J(6, 17) and I(9, 16) is
x = \(\frac{6+9}{2}\) and y = \(\frac{17+16}{2}\)
x = \(\frac{15}{2}\) and y = \(\frac{33}{2}\)
II. The distance of the point P from the Y-axis = 4.
III. A’s coordinates = (1, 8)
S’s coordinates = (15, 8)
Then, AS = |\(\sqrt{(15-1)^2 + (8-8)^2}\)|
= \(\sqrt{14^2}\)
= 14.
OR
The coordinates of A = (1, 8)
The coordinates of B = (4, 10)
Also, m = 1 and n = 3
Then, (x, y) = \(\left(\frac{1 \times 4+3 \times 1}{1+3}, \frac{1 \times 10+3 \times 8}{1+3}\right)\)
= \(\frac{7}{4}, \frac{34}{4}\)
= (1.75, 8.5)

Question 37.
A ladder has rungs 25 cm apart, (see the below).

The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. The top and the bottom rungs are 2\(\frac{1}{2}\) m apart.
I. Find the distance (in cm) from the top to bottom rungs.
II. Find the total number of rungs.
III. The given problem is based on A.E find its first and last term.
OR
What is the length of the wood required for the rungs ?
Answer:
I. Since the top and the bottom rungs are apart by 2\(\frac{1}{2}\) m = \(\frac{5}{2}\)
\(\frac{5}{2}\) × 100 cm
= 250 cm
II. The distance between the two rungs is 25 cm.
Hence, the total number of rungs = \(\frac{250}{25}\) + 1
= 11
III. The length of the rungs increases from 25 to 45 and total number of rungs is 11.
Thus, this is in the form of an A.P., whose first term is 25.
Total number of terms, n = 11
and the last term, T₁₁ = 45
OR
The required length of the wood,
S₁₁ = \(\frac{11}{2}\) [25 + 45]
= \(\frac{11}{2}\) × 70
= 385 cm

Question 38.
A game of chance consists of spinning an arrow which comes of rest pointing at one of the numbers 1,2, 3,4,5,6, 7,8 (see figure) and these are equally likely outcomes.

I. What is the probability that spinning arrow will point at 8?
II. What is the probability that spinning arrow will point at an odd number?
III. What is the probability that spinning arrow will point at a number greater than 2?
OR
What is the probability that spinning arrow will point at a number less than 9?
Answer:
I. Total possible outcomes = 8.
P(getting 8) = \(\frac{1}{8}\)

II. Total odd numbers = 1, 3, 5, 7 = 4
P(getting odd number) = \(\frac{4}{8}\) = \(\frac{1}{2}\).
III. No. greater than 2 = 3, 4, 5, 6, 7, 8 = 6
P(getting no. greater than 2) = \(\frac{6}{8}\) = \(\frac{3}{4}\) .
OR
P(getting no. less than 9) = \(\frac{8}{8}\) = 1.