CBSE Sample Papers for Class 10 Maths Basic Set 4 with Solutions

Practicing the CBSE Sample Papers for Class 10 Maths Basic Set 4 allows you to get rid of exam fear and be confident to appear for the exam.

CBSE Sample Papers for Class 10 Maths Basic Set 4 with Solutions

Time Allowed : 3 hours
Maximum Marks : 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D, and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answer-II (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each) with sub-parts of the values of 1,1 and 2 marks each respectively.
7. All Questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take n = \(\frac{22}{7}\) wherever required if not stated.

Section – A
(Section A consists of 20 Questions of 1 marks each.)

Question 1.
HCF of two consecutive even numbers is :
(A) 0
(B) 1
(C) 2
(D) 4
Answer:
(C) 2

Explanation:
Let the two consecutive even numbers be 2n and (2n + 2).
Prime factorisation of 2n = 2 × n
Prime factorisation of (2n + 2) = 2 × (n + 1)
To find HCF, we multiply all the prime factors common to both numbers.
Therefore, HCF = 2

Question 2.
Given that one of the zeroes of the cubic polynomial ax³ + bx² + cx + d is zero, the sum of the other two zeroes is:
(A) \(\frac{-c}{a}\)
(B) \(\frac{c}{a}\)
(C) 0
(D) \(\frac{-b}{a}\)
Answer:
(D) \(\frac{-b}{a}\)

Explanation :
Let f(x) = ax³ + bx² + cx + d
If a, b, g are the zeroes of f(x), then
α + β + γ = \(\frac{-b}{a}\)
One root is zero (given) so, α = 0.
∴ β + γ = \(\frac{-b}{a}\)

Question 3.
The first four terms of an A.E, whose first term is -3 and the common difference is -3, are :
(A) -3,-6,9,12,15
(B) -3,6,-9,-12,15
(C) -3,-6,-9,-12,-15
(D) -3,-8,-13,-18-12
Answer:
(C) -3,-6,-9,-12,-15

Explanation: In the given A.P, a = – 3, d = – 3,
t_n =a+(n – 1)d
t₁ = ( -3)+(1 – 1)( -3)= -3
t₂ = ( -3) + (2 – 1)( -3) = -o
t₃ = ( -3)+(3 – 1)( -3)= -9
t₄ = ( -3)+(4 – 1)( -3)= -12

Question 4.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :

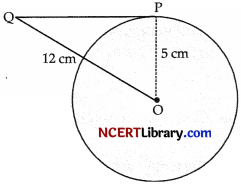
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) \(\sqrt{119}\) cm
Answer:
(D) \(\sqrt{119}\) cm

Explanation :
We know that the radius is perpendicular to tangent
In DOPQ, we have ∠P = 90°
By Pythagoras Theorem,
OQ² = PQ² + OP²
(12)²= PQ² + (5)²
⇒ 144= PQ² + 25
⇒ PQ² = 144 – 25=119
⇒ PQ= \(\sqrt{119}\) cm.

Question 5.
sin 2A = 2 sin A is true when A =
(A) 0°
(B) 30°
(C) 45°
(D) 60°
Answer:
(A) 0°

Explanation:
As sin 2A = sin 0°
2 sin A = 2 sin 0° = 2(0) = 0

Question 6.
The roots of the quadratic equation x² – 2x + 1 =0 are
(A) 1,1
(B) 2,2
(C) -1, -1
(D) 1, -1
Answer:
(A) 1,1

Explanation: We have
x² – 2x + 1 = 0
(x – 1)(x – 1) = 0
x = 1, 1
So the roots of given quadratic equation are 1, 1.

Question 7.
\(\sqrt{3}\) is :
(A) Rational Number
(B) Integer
(C) Irrational Number
(D) None of these
Answer:
(C) Irrational Number

Explanation: 3 is always an irrational number.

Question 8.
If ∆ABC ~ ∆EDF and ∆ABC is not similar to ∆DEE, then which of the following is not true?
(A) BC × EF = AC × FD
(B) AB × EF = AC × DE
(C) BC × DE = AB × EF
(D) BC × DE = AB × FD
Answer:
(C) BC × DE = AB × EF

Explanation:
Since ∆ABC ~ ∆EDF, then we get
\(\frac{A B}{E D}=\frac{A C}{E F}=\frac{B C}{D F}\)
From first two, AB × EF = AC × DE. Option (B) is correct.
From last two, BC × EF = AC × FD. Option (A) is correct.
From first and last, BC × DE = AB × FD. Option (D) is correct.
Thus, option (C) is incorrect.

Question 9.
If the area of a circle is equal to that of a square, then the ratio of their perimeter is :
(A) 22 : 7
(B) \(\sqrt{π}\) : 2
(C) π : 2
(D) \(\sqrt{π}\) : \(\sqrt{2}\)
Answer:
(B) \(\sqrt{π}\) : 2

Explanation:
Let the radius of circle be ‘r’ and side of square be ‘a’.
According to given question,
Area of circle = Area of square
πr² = 4a²
∴ a = \(r \sqrt{π}\) …(i)

So, \(\frac{\text { Perimeter of circle }}{\text { Perimeter of square }}\) = \(\frac{2πr}{4r\sqrt{π}}\) [From equation (i)]
Solving equation (i), we get result as \(\frac{\sqrt{π}}{2}\).

Question 10.
Two identical solid cubes of side 21 are joined end to end. Then total surface area of the resulting cuboid is:
(A) 40l²
(B) 48l²
(C) 64l²
(D) 100l²
Answer:
(A) 40l²
Explanation : Since, cubes are joined from ends,
it gets converted into a cuboid with following
dimensions:
length = 4l, breadth = 2l and height = 2l
∴ The total surface area of obtained cuboid = 2(4l × 2l + 2l × 2l + 2l × 4l)
= 2(8l² + 4l² + 8l²) = 40l² cm2 1

Question 11.
In the formula \(\bar{x}=a+h \frac{\Sigma f_i u_i}{\Sigma f_i}\), for finding the mean of grouped frequency distribution, u_i =
(A) \(\frac{x_i+a}{h}\)
(B) \(h\left(x_i-a\right)\)
(C) \(\frac{x_i-a}{h}\)
(D) \(\frac{a-x_i}{h}\)
Answer:
(C) \(\frac{x_i-a}{h}\)

Explanation:
\(\bar{x}=a+h \frac{\Sigma f_i u_i}{\Sigma f_i}\)
u_i = \(\frac{x_i-a}{h}\)

Question 12.
The probability of getting a bad egg in a lot of 400 is 0.035. The number of bad eggs in the lot is :
(A) 7
(B) 14
(C) 21
(D) 28
Answer:
(B) 14

Explanation:
Total events, T(E) = 400
Number of outcomes favourable for event E, i.e.,
F(E) =?
P(E) = 0.035
∴ P(E) = \(\frac{F(E)}{T(E)}\)
⇒ 0.035 = \(\frac{F(E)}{400}\)
So, F(E) = 0.035 × 400 = 14 eggs.
So, the number of bad eggs are 14.

Question 13.
Area of a sector of angle 45° of a circle with radius R is :
(A) \(\frac{1}{8} \times \pi R\)
(B) \(\frac{\pi r^2}{3}\)
(C) \(\frac{1}{2} \times \pi r^2\)
(D) \(\frac{1}{8} \times \pi R^2\)
Answer:
(D) \(\frac{1}{8} \times \pi R^2\)

Explanation :
We know that area of sector of angle θ
= \(\frac{θ}{360°} \times \pi R^2\)
Area of sector of angle, 45° = \(\frac{45}{360°} \times \pi R^2\)
= \(\frac{1}{8} \times \pi R^2\)

Question 14.
If b = 5, the any integer can be expressed as a =
(A) 5q, 5q + 1, 5q + 2
(B) 5q
(C) 5q + 1
(D) None of these
Answer:
(A) 5q, 5q + 1, 5q + 2

Explanation:
Let a be any positive integer and b = 5
Applying division lemma with a and b = 5, we get
a = 5q + r, where 0 ≤ r ≤ 5
∴ a = 5q + 0 = 5q; a = 5q + 1; a = 5q + 2; a = 5q + 3;
a = 5q + 4; a = 5q + 5 for some integer q.

Question 15.
If P (\(\frac{a}{3}\), 4) is the mid-point of the line segment joining the points Q (-6, 5) and R (-2,3), then the value of a.
(A) -12
(B) 12
(C) 8
(D) – 8
Answer:
(A) -12

Explanation:
Given that,
P (\(\frac{a}{3}\), 4), is the mid-point of the line segment
joining the points Q (-6, 5) and R (2, 3).

Now, mid-point of a line segment joining two points (x₁, y₁) and (x₂, y₂) is given by,
\(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)
∴ Mid-point of = P \(\frac{a}{3}\)
= P (-4,4)
But the coordinates of mid-point P are given as (\(\frac{a}{3}\), 4).
∴ (\(\frac{a}{3}\), 4) = (-4,4)
Comparing the coordinates, we get
\(\frac{a}{3}\)= -4 or a = -12

Question 16.
The distances of the point P(-7, 5) from the x-axis and y-axis are :
(A) -7,5
(B) 5,-7
(C) 7,5
(D) 7
Answer:
(B) 5,-7

Explanation :
The distance from X-axis is equal to its ordinate i.e., 5
The distance from y-axis is equal to its obscissa i.e., -7.

Question 17.
The value of (sec A + tan A) (1 – sin A) is :
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
Answer:
(D) cos A

Explanation:

Question 18.
If the height of a vertical pole is \(\sqrt{3}\) times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is :
(A) 30°
(B) 60°
(C) 45°
(D) 75°
Answer:
(B) 60°

Explanation :
Let the length of shadow is x,
Then height of pole = \(\sqrt{3}\) x

tan θ = \(\sqrt{3}\)
tan θ = tan 60°
θ = 60°.

Directions for questions 19 & 20: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer.
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true but (R) is NOT the correct explanation of (A).
(C) (A) is true but (R) is false. .
(D) (A) is false and (R) is true.

Question 19.
Assertion (A): If the ratio of the length of a vertical rod and the length of its shadow is 1 : \(\sqrt{3}\), then the angle of elevation of the Sun at that moment is 30°.
Reason (R): If the ratio of the height of a tower and the length of its shadow on the ground is \(\sqrt{3}\) :1, then the angle of elevation of the sun is 60°.
Answer:
Option (B) is correct.

Explanation :
In case of assertion:
Let AB be a vertical rod and BC be its shadow.
From the figure, ∠ACB = θ.
In DABC,

⇒ tan θ = tan 30°
S olut ions 3
⇒ θ = 30°
∴ Assertion is correct.
In case of reason:

Let the height of tower be AB and its shadow be BC.
\(\frac{BC}{AB}\) = tan θ
= \(\frac{\sqrt{3}}{1}\)
= tan 60°
Hence, the angle of elevation of Sun = 60°.
∴ Reason is correct.
Hence, both assertion and reason are correct but
reason is not the correct explanation for assertion.

Question 20.
Assertion (A): If D is a point on side QR of ∆PQR such that PD ⊥ QR, then ∆PQD ~ ∆RPD.
Reason (R): In the figure given below, if ∠D = ∠C then ∆ADE ~ ∆ACB.

Answer:
(D) (A) is false and (R) is true.

Explanation :
In case of assertion:

In ∆PQD and ∆RPD, ∠PDQ = ∠PDR = 90° .
There is no other information to be similar. Thus,
it will be not correct to say that ∆PQD ~ ∆RPD.
∴ Assertion is incorrect.
In case of reason:
In ∆ADE and ∆ACB, we have
∠ADE = ∠ACB [Given]
∠DAE = ∠CAB [Common angle]
By AA similarity, we get ∆ADE ~ ∆ACB.
∴ Reason is correct
Hence, assertion is incorrect but reason is correct

Section – B
Section B consists of 5 Questions of 2 marks each.

Question 21.
Find all the zeroes of f(x) = x² – 2x.
OR
Find whether the following pair of linear equations is consistent or inconsistent:
3x + 2y = 8 and 6x – 4y = 9
Answer:
Given, f(x) = x² – 2x.
= x (x – 2)
f (x) = 0
⇒ x = 0 or x = 2
Hence, zeroes are 0 and 2.
OR
Since,
\(\frac{3}{6} \neq \frac{2}{-4}\)
i.e., \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
Hence, the pair of linear equations is consistent.

Question 22.
In figure., PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then find the length of each tangent.

Answer:
Here, CAPB will be a square.
Then, CA = AP = PB = BC = 4 cm
∴ Length of tangent = 4 cm.

Question 23.
In given figure, D is a point on AC such that AD = 2 CD, also DE || AB. Prove that ∆CAB ~ ∆CDE.

Answer:
Given AD = 2CD
In ∆CDE and ∆CAB
∠C = ∠C (Common)
∠CDE = ∠CAB
(Corresponding angles)
∴ ∆CDE ~ ∆CAB (By AA similarity rule)
Hence Proved.

Question 24.
If 1 + sin² θ = 3 sin θ cos θ, prove that tan θ = 1 or \(\frac{1}{2}\).
Answer
Given, 1 + sin² θ = 3 sin θ cos θ
On dividing by sin² θ on both sides, we get
\(\frac{1}{sin² θ}\) + 1 = 3 cot θ
[∵ cot θ = \(\frac{cos θ}{sin θ}\)]
⇒ cosec² θ + 1 = 3 cot θ
⇒ 1 + cot² θ + 1 = 3 cot θ
⇒ cot² θ – 3 cot θ + 2 = 0
⇒ cot² θ – 2 cot θ – cot θ + 2 = 0
⇒ cot θ(cot θ – 2) – 1(cot θ – 2) = 0
⇒ (cot θ – 2)(cot θ – 1) = 0
If cot θ = 1 or 2
Then, tan θ = 1 or \(\frac{1}{2}\).
Hence Proved.

Question 25.
In the given figure, find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC = 40°. [Use π =\(\frac{22}{7}\)]

OR
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm, find the volume of the cylinder.[Use π =\(\frac{22}{7}\)]
Answer:

Radius of inner circle =7 cm
Radius of outer circle = 14 cm
and ∠AOC = 40°
m ∠AOC = 360° – 40° = 320°
Area of shaded region

OR
Here r + h = 37 and 2πr(r + h) = 1628
or, 2πr × 37 = 1628
or, 2πr = \(\frac{1628}{37}\)
or, r = 7 cm
and h = 30 cm
Hence, volume of cylinder = πr²h
= \(\frac{22}{7}\) × 7 × 7 × 30
= 4620 cm³

Section – C
Section C consists of 6 Questions of 3 marks each.

Question 26.
Find the greatest number of six digits exactly divisible by 18,24 and 36.
OR
Prove that 2 +5 \(\sqrt{5}\) is an irrational number, given that Vs is an irrational number.
LCM of 18, 24 and 36
18 = 2 × 32
24 = 23 × 3
36 = 22 × 32
LCM (18, 24, 36) = 23 × 32 ⇒ 72
The largest 6 digit number is 999999.

63 → Remainder
∴ The required number
= 9,99,999 – 63
= 9,99,936.
OR
Let 2 + 5 \(\sqrt{5}\) = a, where ‘a’ is a rational number.
then 5 \(\sqrt{5}\) = a – 2
\(\sqrt{5}=\frac{a – 2}{5}\)
Which is a contradiction as LHS is irrational and RHS is rational. ½
∴ 2 + 5 \(\sqrt{5}\) can not be rational
Hence, 2 + 5 \(\sqrt{5}\) is irrational.
Alternate method :
Let 2 + 5 \(\sqrt{5}\) be rational numbers in the form \(\frac{p}{q}\)
∴ 2 + 5 \(\sqrt{5}\) = \(\frac{p}{q}\),(p, q are integers, q ≠ 0)
⇒ \(\sqrt{5}\) = \(\frac{p}{q}-2\)÷ 5 = \(\frac{p-2q}{5q}\)
LHS is irrational and RHS is rational which is a contradiction.
∴ 2 + 5\(\sqrt{5}\) is irrational.

Question 27.
A man repays a loan of ₹ 3250 by paying ₹ 20 in the first month and then increases the payment by ₹ 15 every month. How long will it take him to clear the loan ?
OR
Solve for x:
2x² + 6\(\sqrt{3}\)x – 60 = 0
Answer:
Here, a = 20, d = 15
and S_n = 3250
Then, S_n = \(\frac{n}{2}\)[2a+(n-1)d]
or, 3250 = \(\frac{n}{2}\)[2a+(n-1)×15]
or, 3250 × 2 = n[40 + 15n – 15]
or, 6500 = n[25 + 15n]
or, 1300 = n[5 + 3n]
or, 3n² + 5n – 1300 = 0
or, 3n² + 65n – 60n – 1300 = 0
or, n(3n + 65) – 20(3n + 65) = 0
or, (n – 20)(3n + 65) = 0 1
Either n = \(– \frac{65}{3}\), (not possible)
or n = 20
Thus, man will repay loan in 20 months.
OR
Given,
2x² + 6\(\sqrt{3}\)x – 60 = 0
⇒ x² + 3 \(\sqrt{3}\) – 30 = 0
⇒ x² + 5 \(\sqrt{3}\) – 2 \(\sqrt{3}\)x – 30 = 0
⇒ x(x+ 5 \(\sqrt{3}\)) – 2 \(\sqrt{3}\)(x – 2 \(\sqrt{3}\)) = 0
⇒ (x+ 5 \(\sqrt{3}\))(x – 2 \(\sqrt{3}\)) = 0
⇒ x = – 5 \(\sqrt{3}\) or 2 \(\sqrt{3}\)

Question 28.
If m^th term of A.E is \(\frac{1}{n}\) and n^th term is \(\frac{1}{m}\) , find the sum of first mn terms.
Answer:
Let first term of given A.P. be a and common difference be d.
∴ a_m = a + (m – 1)d = \(\frac{1}{n}\)…(i)
and a_n = a + (n – 1)d = \(\frac{1}{m}\)…(ii)
On subtracting (ii) from (i) we get

Hence, the sum of first mn terms = \(\frac{1}{2}\)(mn + 1).

Question 29.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Answer:
Given: A circle with centre O is inscribed in a
quadrilateral ABCD.
In ∆AEO and ∆AFO,
OE = OF [radii of circle]
∠OEA = ∠OFA = 90°
[radius is ⊥r to tangent]

The point of contact is perpendicular to the tangent.
OA = OA [common side]
∆AEO ≅ ∆AFO [By RHS]
∠7 = ∠8 (By cpct) …(i)
Similarly,
∠1 = ∠2 …(ii)
∠3 = ∠4 …(iii)
∠5 = ∠6 …(iv)
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
[angle around a point]
2∠1 + 2 ∠8 + 2 ∠4 + 2 ∠5 = 360°
∠1 + ∠8 + ∠4 + ∠5 = 180°
(∠1 + ∠8) + (∠4 + ∠5) = 180°
∠AOB + ∠COD = 180°
Hence Proved.

Question 30.
From the top of tower, 100 m high, a man observes two cars on the opposite sides of the tower with the angles of depression 30° & 45° respectively. Find the distance between the cars. (Use \(\sqrt{3}\) = 1.73)
Answer:

In right ∆ADC,
tan 30° = \(\frac{C D}{A D}\)
⇒\(\frac{1}{\sqrt{3}}=\frac{100}{x}\)
⇒ x = 100 \(\sqrt{3}\) …(i)
In right ∆BDC,
tan 45° = \(\frac{C D}{D B}\)
⇒ 1 = \(\frac{100}{y}\)
⇒ y = 100 m
Distance between two cars
= AB = AD + DB
= (100 \(\sqrt{3}\) + 100) m
= (100 × 1.73 + 100) m
= (173 + 100) m
= 273 m
Hence, distance between two cars = 273 m

Question 31.
The angle of elevation of a cloud from a point 120 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
Answer:
In right ∆APO, tan 30° = \(\frac{H – 120}{OP}\)
\(\frac{1}{\sqrt{3}}=\frac{H – 120}{OP}\)
⇒ OP = (H – 120) \(\sqrt{3}\) …(i) 1
In ∆OPA’, tan 60° = \(\frac{H + 120}{OP}\)

⇒ OP = \(\frac{H + 120}{\sqrt{3}}\) …(ii) 1
From (i) and (ii), we get
\(\frac{H + 120}{\sqrt{3}}\) = \(\sqrt{3}\)(H – 120)
So, height of cloud H= 240 m.

Section – D
Section D consists of 4 Questions of 5 marks each.

Question 32.
A motor boat can travel 30 km upstream and 28 km downstream in 7 hours. It can travel 21 km upstream and return in 5 hours. Find the speed of the boat in still water and the speed of the stream.
OR
If (-5) is a root of the quadratic equation 2x² + px + 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots, then find the values of p and k.
Answer:
Let the speed of the boat in still water be ‘x’
km/hr and speed of the stream be ‘y’ km/h
∴ Speed of boat up stream = (x – y) km/h
Speed of boat down stream = (x + y) km/h
∴ \(\begin{aligned}
& \frac{30}{x-y}+\frac{28}{x+y}=7 \\
& \frac{21}{x-y}+\frac{21}{x+y}=5
\end{aligned}\)
Let \(\frac{1}{x-y}\) = a and \(\frac{1}{x+y}\) = b, then
30a + 28b = 7 …(i)
and 21a + 21b = 5 …(ii)
Multiplying eqn. (i) by 3 and eqn. (ii) by 4 and then subtracting,
90a + 84b = 21 …(iii)
84a + 84b = 20 …(iv)

Putting this value of a in eqn (i), we get
30 × \(\frac{1}{6}\) + 28b = 7
28b = 7 – 30 × \(\frac{1}{6}\) ⇒ 2
∴ b = \(\frac{1}{4}\)
x + y = 14 …(iv)
Now, a = \(\frac{1}{x-y}\) ⇒ \(\frac{1}{6}\)
⇒ x – y = 6 …(v)
Solving eqns. (v) and (iv), we get
x = 10 and y = 4
Hence, speed of the boat in still water = 10 km/h
and speed of the stream = 4 km/h.
OR
Since, (-5) is a root of given quadratic equation 2x² + px – 15 = 0, then
2(-5)² + p(-5) -15 = 0
50 – 5p – 15 = 0
5p = 35 ⇒ p = 7
Now, p(x² + x) + k = 0 has equal roots
px² + px + k = 0
So, (b)² – 4ac = 0
(p)² – 4p×k = 0
(7)² – 4 × 7 × k = 0
28k = 49
k = \(\frac{49}{28}\) ⇒ \(\frac{7}{4}\)
Hence, p = 7 and k = \(\frac{7}{4}\).

Question 33.
In the figure, PQ is a tangent to a circle with centre O. If ∠OAB = 30°, find ∠ABP and ∠AOB.

Answer:
In ∆OAB, OB = OA (radius of a circle)
Then, ∆OAB = ∆OBA
∠OBA = 30°
∴ ∠AOB = 180° – (30° + 30°)
∴ ∠AOB = 120°
∠ABP = ∠OBP – ∠OBA
= 90° – 30° = 60°

Question 34.
The table shows the daily expenditure on grocery of 25 households in a locality. Find the modal daily expenditure on grocery by a suitable method.

Daily Expenditure (in ₹)	100 -150	150-200	200-250	250 – 300	300-350
No of households	4	5	12	2	2

OR
The maximum bowling speeds, in km per hour, of 33 players at a cricket coaching centre are given as follows.

Speed (in km/h)	85-100	100-115	115-130	130-145
Number of players	11	9	8	5

Calculate the median bowling speed.
Answer:
200 – 250 is the modal class.
\(\text { Mode }=l+\left[\frac{f_1-f_0}{2 f_1-f_0-f_2}\right] h\)
= \(200+\left[\frac{12-5}{24-5-2}\right] ×50\)
= 200 + 20.59 = ₹ 220.59
OR
To calculate median, we form c.f. table.

Speed (in km/h) C.I.	Number of players (f)	c.f.
85-100	11	11
100-115	9	20
115-130	8	28
130-145	5	33

N = Number of observations = 33 (Odd)
Median of 33 observations = 17th observation,
which lies in class 100-115
l = 100, f = 9, c.f. = 11, h = 100 – 85 = 15

Hence, the median bowling speed is 109.17 km/h.

Question 35.
Isha is 10 years old girl. On the result day, Isha and her father Suresh were very happy as she got first position in the class. While coming back to their home, Isha asked for a treat from her father as a reward for her success. They went to a juice shop and asked for two glasses of juice.
Aisha, a juice seller, was serving juice to her customers in two type of glasses. Both the glasses had inner radius 3 cm. The height of both the glasses was 10 cm.
First type: A Glass with hemispherical raised bottom.

Second type: A glass with conical raised bottom of height 1.5 cm.
Isha insisted to have the juice in first tvpe of glass and her father decided to have the juice in second type of glass. Out of the two, Isha or her father Suresh, who got more quantity of juice to drink and by how much ?
Answer:
Capacity of first glass = πr²H – \(\frac{2}{3}\)πr³
= π × 9(10 – 2)
= 72π cm³
Capacity of second glass = πr²H – \(\frac{1}{3}\)πr²h
= π × 3 × 3(10 – 0.5)
= 85.5π cm³
∵ Suresh got 42.39 cm³ more quantity of juice.

Detailed Solution:
In case of first type glass, we have
radius (r) = 3 cm
Height (H) = 10 cm
Capacity of Juice in cylindrical part
= πr²H
= π × (3)³ × 10

Capacity of hemispherical part
= \(\frac{2}{3}\)πr³
= \(\frac{2}{3}\)π ×(3)³

∴ Capacity of Juice in first glass

In case of second glass, we have
radius of base (r) = 3 cm
height of bottom part (h) = 1.5 cm
∴ Capacity of conical part

Since, Suresh used second glass for drinking juice, so he got more quantity of juice.
i.e., Suresh got 268.47 – 226.08 = 42.39 cm3 more juice than Isha.

Section – E
Case study based questions are compulsory.

Question 36.
Shreya purchased a new table from market with her mother. The top of the table is hexagonal in shape as shown in the given figure.

I. Find the coordinates of points H and G.
II. Write one pair of points which have same ordinate.
III. Find the distance between the points A and B.
OR
Find the coordinates of the line joining points M and Q.
Answer:
I. Coordinates of point H = (1, 5)
Coordinates of point G = (5, 1)

II. Points T and O has same ordinates i.e., T = (3, 9) and O = T = (11, 9)

III. Coordinates of points A = (1, 9)
Coordinates of point B = (5, 13)
Distance, d = \(\sqrt{(1-5)^2 + (9-13)^2}\) \(\sqrt{16^2 + 16^2}\)
= \(\sqrt{32}\) = \(4 \sqrt{32}\) units
OR
Coordinates of point M = (5, 11)
Coordinates of point Q = (9, 3)
Mid-point = \(\frac{5+9}{2}, \frac{11+3}{2}\) = (7, 7)

Question 37.
There is a triangular playground as shown in the below figure. Many children and people are playing and walking in the ground.

As we see in the above figure of right angled triangle playground, the length of the sides are 5x cm and (3x – 1) cm and area of the triangle is 60 cm².
I. Find the value of x.
OR
Find the length of AC.
II. Find the perimeter of ∆ABC.
III. The given problem is based on which mathematical concept ?
Answer:
I. Given, area of triangle = 60 cm²
⇒ \(\frac{1}{2}\) × AB × BC = 0
⇒ (5x)(3x – 1) = 120
⇒ 3x² – x – 24 = 0
⇒ 3x² – 9x + 8x – 24 = 0
⇒ 3x(x – 3) + 8(x – 3) = 0
⇒ (x – 3)(3x + 8) = 0
Either x = 3 or x = \(– \frac{8}{3}\)
Since length can’t be negative, then x = 3.
OR
AB = 5 × 3 = 15 cm and
BC = (3x – 1) cm
= (3 × 3 – 1) cm
= 8 cm 1
Now, in right angled ∆ABC,
AC² = AB² + BC²
(By using Pythagoras theorem)
= (15)²+ (8)² = 225 + 64
= 289 = (17)²
Hence, AC = 17 cm

II. Here, AB = 15 cm, BC = 8 cm and AC = 17 cm.
Then, the perimeter of ∆ABC = (AB + BC + CA) cm
= (15 + 8 + 17) cm
= 40 cm

III. The given problem is based on the concept of quadratic equations.

Question 38.
100 m RACE
A stopwatch was used to find the time that it took a group of students to run 100 m.

Time (in sec)	0-20	20-40	40-60	60-80	80-100
No. of students	8	10	13	6	3

I. Estimate the mean time taken by a student to finish the race.
OR
Find the sum of lower limits of median class and modal class.
II. How many students finished the race within 1 minute?
III. How many students finished the race within 30 sec?
Answer:
I.

Time (in sec)	x	f	cf	fx
0-20	10	8	8	80
20-40	30	10	18	300
40-60	50	13	31	650
60-80	70	6	37	420
80-100	90	3	40	270
Total		40		1720

Mean = \(\frac{1720}{40}\)= 43
OR
Median class = 40 – 60
Modal class = 40 – 60
Therefore, the sum of the lower limits of median and modal class = 40 + 40 = 80

II. Number of students who finished the race within 1 minute = 8 + 10 + 13 = 31
III. No. of students who finished the race within 30 sec = 8 + 10 = 18.