CBSE Previous Year Question Papers Class 12 Maths 2016 Outside Delhi

CBSE Previous Year Question Papers Class 12 Maths 2016 Outside Delhi

Time allowed: 3 hours
Maximum marks : 100

General Instructions:

• All questions are compulsory.
• The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
• All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
• There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
• Use of calculators is not permitted. You may ask for logarithmic tables, if required.

**Answer is not given due to the change in present syllabus

CBSE Previous Year Question Papers Class 12 Maths 2016 Outside Delhi Set I

Section – A

Question 1.
If x ϵ N and \(\left|\begin{array}{cc}{x+3} & {-2} \\ {-3 x} & {2 x}\end{array}\right|\) = 8, then find the value of x. [1]
Solution:
We have, \(\left|\begin{array}{cc}{x+3} & {-2} \\ {-3 x} & {2 x}\end{array}\right|\) = 8
⇒ (x + 3) × 2x – (-2) × (-3x) = 8
⇒ 2x² + 6x – 6x = 8
⇒ 2x² = 8
⇒ x² = 4
But x ≠ -2 as x ϵ N
⇒ x = 2

Question 2.
Use elementary column operation C₂ → C₂ + 2C₁ in the following matrix equation : [1]

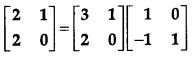
Solution:
We have

Question 3.
Write the number of all possible matrices of order 2 × 2 with each entry 1, 2 or 3. [1]
Solution:
Total number of all possible matrices of order 2 × 2 with each entry 1, 2 or 3 are 3⁴ i.e., 81.

Question 4.
Write the position vector of the point which divides the join of points with position vector \(3 \vec{a}-2 \vec{b} \text { and } 2 \vec{a}+3 \vec{b}\) in the ratio 2 : 1. [1]
Solution:
Let A and B be the given points with position vectors \(3 \vec{a}-2 \vec{b} \text { and } 2 \vec{a}+3 \vec{b}\) respectively.
Let P and Q be the points dividing AB in the ratio 2:1 internally and externally respectively. Then,

Question 5.
Write the number of vectors of unit length perpendicular to both the vectors \(\vec{a}=2 \hat{i}+\hat{j}+2 \hat{k} \text { and } \vec{b}=\hat{j}+\hat{k}\). [1]
Solution:
We know that the unit vectors perpendicular to the plane of \(\vec{a} \text { and } \vec{b}\) are

Question 6.
Find the vector equation of the plane with intercepts 3,-4 and 2 on x, y and z-axis respectively. [1]
Solution:
The equation of the required plane is,

This is the vector equation of the plane with intercept 3,-4 and 2 on coordinate axis.

Section- B

Question 7.
Find the coordinates of the point where the line through the points A(3, 4, 1) and B(5, 1, 6) crosses the XZ-plane. Also find the angle which this line makes with the XZ-plane. [4]
Solution:
The equation of the line passing through A and B is,

Question 8.
The two adjacent sides of a parallelogram are \(2 \hat{i}-4 \hat{j}-5 \hat{k} \text { and } 2 \hat{i}+2 \hat{j}+3 \hat{k}\). Find the two unit vectors parallel to its diagonals. Using the diagonal vectors, find the area of the parallelogram. [4]
Solution:
Let ABCD be a parallelogram such that

Question 9.
In a game, a man wins ₹ 5 for getting a number greater than 4 and loses ₹ 1 otherwise, when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a number greater than 4. Find the expected value of the amount he wins/loses. [4]
Solution:
Let n denote the number of throws required to get a number greater than 4 and X denote the amount won/lost.
The man may get a number greater than 4 in the very first throw of the die or in second throw or in the third throw.
Let p = Probability of getting a number greater than 4

OR
A bag contains 4 balls. Two balls are drawn at random (without replacement) and are found to be white. What is the probability that all balls in the bag are white ?
Solution:
We know that the number of white balls can’t be less than 2.
Now, there are different cases, for the number of white balls in the bag. The total cases are ²C₂ + ³C₂ + ⁴C₂.

Question 10.
Differentiate x^sinx + (sin x)^cosx with respect to x. [4]
Solution:
We have,

OR
If y = 2 cos(log x) + 3 sin(log x), prove that

Solution:
Given, y = 2 cos (log x) + 3 sin (log x) On differentiating both sides w.r.t. x, we get

Question 11.
If x = a sin 2t (1 + cos 2t) and y = b cos 2t (1 – cos 2t), find \(\frac{d y}{d x}\) at t = \(\frac{\pi}{4}\). [4]
Solution:
We have, x = a sin 2t (1 + cos 2t)

Question 12.
The equation of tangent at (2, 3) on the curve y² = ax³ + b is y = 4x – 5. Find the value of a and b. [4]
Solution:
Since the point (2, 3) lies on the curve y² = ax³ + b

Question 13.
Find: [4]

Solution:
Let,

Question 14.
Evaluate: [4]

Solution:
We have,


OR
Evaluate:

Solution:

Question 15.
Find: [4]

Solution:

Question 16.
Solve the differential equation: [4]

Solution:

Question 17.
Form the differential equation of the family of circles in the second quadrant and touching the coordinate axes. [4]
Solution:
The equation of circles in the second quadrant which touch the coordinate axes is
(x + a)² + (y – a)² = a², a ϵe R …(i)

where a is a parameter. This equation contains one arbitrary constant. So we shall differentiate it once only and we shall get a differential equation of first order.
Differentiating (i) w. r. t. x, we get

This is the required differential equation representing the given family of circles.

Question 18.
Solve the equation for x : sin^-1 x + sin^-1 (1 – x) = cos^-1 x. [4]
Solution:


OR

Solution:

Question 19.
A trust invested some money in two types of bond. The first bond pays 10% interest and second bond pays 12% interest. The trust received ₹ 2,800 as interest. However, if trust had interchanged money in bonds, they would have got ₹ 100 less as interest. Using matrix method, find the amount invested by the trust. Interest received on this amount will be given to Helpage India as donation. Which value is reflected in this question ? [4]
Solution:
Let the amount invested by the trust in first and second bond be x and y respectively.

Section – C

Question 20.
There are two types of fertilisers ‘A’ and ‘B’. ‘A’ consists of 12% nitrogen and 5% phosphoric acid whereas ‘B’ consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If ‘A’ costs ₹ 10 per kg and ‘B’ cost ₹ 8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost. [6]
Solution:
Let the quantity of fertiliser A and B be x and y respectively.
To minimize : Z = ₹ (10x + 8y)
Subject to the constraints :


So, Z is minimum for x = 30 and y = 210 and the minimum value of Z is ₹ 1980.
Hence, the quantity of fertilizer A is 30 kg and of fertilizer B is 210 kg.

Question 21.
Five bad oranges are accidently mixed with 20 good ones. If four oranges are drawn one by one successively with replacement, then find the probability distribution of number of bad oranges drawn. Hence find the mean and variance of the distribution. [6]
Solution:
Let X denotes the number of bad oranges in a draw of 4 oranges from a group of 20 good oranges and 5 bad oranges. Since there are 5 bad oranges in the group, therefore X can take values, 0, 1, 2, 3, 4.
Now, P(X = 0) = Probability of getting no bad orange.
P(X = 0) = Probability of getting 4 good oranges

Question 22.
Find the position vector of the foot of perpendicular and the perpendicular distance from the point P with position vector \(2 \hat{i}+3 \hat{j}+4 \hat{k}\) to the plane \(\vec{r} \cdot(2 \hat{i}+\hat{j}+3 \hat{k})-26=0\). Also find image of P in the plane. [6]
Solution:
Let L be the foot of the perpendicular

Question 23.
Show that the binary operation * on A = R – {-1} defined as a * b = a + b + ab for all a, b ϵ A is commutative and associative on A. Also find the identity element of * in A and prove that every element of A is invertible.** [6]

Question 24.
Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is \(6 \sqrt{3} r\)r. [6]
Solution:
Let ABC be an isosceles triangle with AB = AC and a circle with centre O and radius r, touching sides AB, BC, CA at D, F, E respectively.





OR
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is \(\frac{\pi}{3}\).
Solution:
Let ABC be a right angled triangle with base BC = x, AB = y such that x + y = k (constant).
Let A be the angle between base and hypotenuse.
Let A be the area of the tringle. Then,

Question 25.
Prove that the curves y² = 4x and x² = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts. [6]
Solution:
Let A₁, A₂ and A₃ denote areas OSPQO, OSPTO and OTPRO respectively.
To prove : A₁ = A₂ = A₃,

Question 26.
Using properties of determinants, show that ∆ABC is isosceles if: [6]

Solution:
We have,

⇒ Expanding along R₁ (cos B – cos A) (cos C – cos A) [1 + cos A + cos C – 1 – cos A – cos B] = 0
⇒ (cos B – cos A) (cos C – cos A) (cos C – cos B) = 0
Either cos B = cos A or cos C = cos A or cos C = cos B
i.e., either BC = AC or BC = AB or AC = AB
Hence, ∆ ABC is isosceles. Hence Proved.
OR
A shopkeeper has 3 varieties of pens ‘A’, ‘B’ and ‘C’. Meenu purchased 1 pen of each variety for a total of ₹ 21. Jeevan purchased 4 pens of ‘A’ variety, 3 pens of ‘B’ variety and 2 pens of ‘C variety for ₹ 60. While Shikha purchased 6 pens of ‘A’ variety, 2 pens of ‘B’ variety and 3 pens of ‘C’ variety for ₹ 70. Using matrix method, find cost of each variety of pen.
Solution:
Let the cost of each variety of pen be ₹ x, ₹ y and ₹ z respectively. Then,
x + y + z = 21
4x + 3y + 2z = 60
and 6x + 2y + 3z = 70
This system of equations can be written in matrix form as follows:




Hence, the cost of each variety of pen are ₹ 5, ₹ 8 and ₹ 8 respectively.

All questions are same in Outside Delhi Set II and Set III

CBSE Previous Year Question Papers