CBSE Class 12 Physics Question Paper 2019

CBSE Class 12 Physics Question Paper 2019

General Instruction :

(i) All questions are compulsory. There are 27 questions in all.
(ii) This question paper has four sections : Section A, Section B, Section C, Section D.
(iii) Section A contain five questions of one mark each. Section B contains seven questions of two marks each, Section C contains twelve questions of three marks each, Section D contains three questions offive marks each.
(iv) There is no overall choice. However, an internal choice(s) has been provided in two question of one marks, two question of two marks, four questions of three marks weightage. You have to attempt only one of the choices in such questions.
(v) You may use the following values of physical constants wherever necessary :
\(\begin{array}{l}{\mathrm{c}=3 \times 10^{8} \mathrm{m} / \mathrm{s}} \\ {\mathrm{h}=6.63 \times 10^{-34} \mathrm{Js}} \\ {\mathrm{e}=1.6 \times 10^{-19} \mathrm{C}} \\ {\mu_{0}=4 \pi \times 10^{-7} \mathrm{T} \mathrm{mA}^{-1}} \\ {\varepsilon_{0}=8.854 \times 10^{-12} \mathrm{C}^{2} \mathrm{N}^{-1} \mathrm{m}^{-2}} \\ {\frac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9} \mathrm{N} \mathrm{m}^{2} \mathrm{C}^{-2}} \\ {\mathrm{m}_{\mathrm{e}}=9.1 \times 10^{-31} \mathrm{kg}}\end{array}\)
Mass of Neutrons = 1.675 × 10^–27 kg
Mass of proton = 1.673 × 10^–27kg
Avogadro’s number = 6.023 × 10²³ per gram mole
Boltzmann constant = 1.38 × 10^–23 JK^–1

SECTION A

Question 1.
Draw equipotential surfaces for an electric dipole. [1]
Solution:

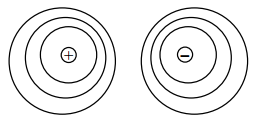
Question 2.
A proton is accelerated through a potential difference V, subjected to a uniform magnetic field acting normal to the velocity of the proton. If the potential difference is doubled, how will the circular path described by the proton in the magnetic field change ? [1]
Solution:

Question 3.
The magnetic susceptibility of magnesium at 300 K is 1.2 × 10⁵. At what temperature will its magnetic susceptibility become 1.44 × 10⁵ ? [1]
OR
The magnetic susceptibility χ of a given material is – 0.5. Identify the magnetic material.
Solution:

OR
Diamagnetic

Question 4.
Identify the semiconductor diode whose V-I characteristics are as shown. [1]

Solution:
Photo-Diode

Question 5.
Which part of the electromagnetic spectrum is used in RADAR? Give its frequency range. [1]
OR
How are electromagnetic waves produced by accelerating charges?
Solution:
3KHz – 300 GHz
OR
By accelerating charge particle produce changing E & B field.

SECTION B

Question 6.
A capacitor made of two parallel plates, each of area ‘A’ and separation ‘d’ is charged by an external dc source. Show that during charging, the displacement current inside the capacitor is the same as the current charging the capacitor. [2]
Solution:

Question 7.
A photon and a proton have the same de-Broglie wavelength λ. Prove that the energy of the photon is
(2mλc/h) times the kinetic energy of the proton. [2]
Solution:
E = hν → Photon
\(\begin{array}{l}{\mathrm{\lambda}=\frac{\mathrm{h}}{\mathrm{P}}} \\ {\mathrm{P}=\frac{\mathrm{h}}{\lambda}} \\ {\mathrm{mV}=\frac{\mathrm{h}}{\lambda}} \\ {\mathrm{V}=\frac{\mathrm{h}}{\lambda \mathrm{m}}} \\ {\mathrm{E}=\frac{\mathrm{hC}}{\lambda}}\end{array}\)
Kinetic energy of proton
\(\begin{aligned} \mathrm{k} &=\frac{1}{2} \mathrm{mV}^{2} \\ \mathrm{k} &=\frac{1}{2} \mathrm{m}\left(\frac{\mathrm{h}}{\lambda \mathrm{m}}\right)^{2} \\ \mathrm{k} &=\frac{1}{2} \frac{\mathrm{h}^{2}}{\lambda^{2} \cdot \mathrm{m}} \\ \frac{\mathrm{E}}{\mathrm{k}}=\frac{\frac{\mathrm{hC}}{\lambda}}{\frac{\mathrm{h}^{2}}{2 \lambda^{2} \mathrm{m}}} &=\frac{2 \mathrm{mC\lambda}}{\mathrm{h}} \end{aligned}\)

Question 8.
A photon emitted during the de-excitation of electron from a state n to the first excited state in a hydrogen atom, irradiates a metallic cathode of work function 2 eV, in a photo cell, with a stopping potential of 0.55 V. Obtain the value of the quantum number of the state n. [2]
OR
A hydrogen atom in the ground state is excited by an electron beam of 12.5 eV energy. Find out the maximum number of lines emitted by the atom from its excited state.
Solution:

OR
This beam can excite atom upto n = 3
Thus maximum no. of lines \(=\frac{3(3-1)}{2}=3\)

Question 9.
Draw the ray diagram of an astronomical telescope showing image formation in the normal adjustment position. Write the expression for its magnifying power. [2]
OR
Draw a labelled ray diagram to show image formation by a compound microscope and write the expression for its resolving power.
Solution:

OR

Resolving power \(=\frac{2 \mu \sin \beta}{1.22 \lambda}\)

Question 10.
Write the relation between the height of a TV antenna and the maximum range up to which signals transmitted by the antenna can be received. How is this expression modified in the case of line of sight communication by space waves? In which range of frequencies, is this mode of communication used? [2]
Solution:

\(\mathrm{d}=\sqrt{2 \mathrm{RH}_{\mathrm{T}}}+\sqrt{2 \mathrm{RH}_{\mathrm{T}}}\)
Frequency range should be greater than 40 MHz.

Question 11.
Under which conditions can a rainbow be observed? Distinguish between a primary and a secondary rainbow. [2]
Solution:
Condition :
(1) There must be rain showers
(2) Observer back must be face the sun
Primary                                             Secondary
(a) One Tir & two refraction           (a) Two TIR & two refraction
(b) Brighter                                        (b) Comparatively less bright

Question 12.
Explain the following : [2]
(a) Sky appears blue.
(b) The Sun appears reddish at
(i) sunset,
(ii) sunrise.
Solution:
(a) Sky appears blue due to scattering of light the water droplet size around the wavelength of violet & blue colour.
(b) (i) due to long distance travel by white light red colour reached only
(ii) due to long distance travel by white light red colour reached only

SECTION C

Question 13.
A capacitor (C) and resistor (R) are connected in series with an ac source of voltage of frequency 50 Hz. The potential difference across C and R are respectively 120 V, 90 V, and the current in the circuit is 3 A. Calculate
(i) the impedance of the circuit
(ii) the value of the inductance, which when connected in series with C and R will make the power factor of the circuit unity. [3]
OR
The figure shows a series LCR circuit connected to a variable frequency 230 V source.

(a) Determine the source frequency which drives the circuit in resonance.
(b) Calculate the impedance of the circuit and amplitude of current at resonance.
(c) Show that potential drop across LC combination is zero at resonating frequency.
Solution:

Question 14.
Give reason to explain why n and p regions of a Zener diode are heavily doped. Find the current through the Zener diode in the circuit given below : (Zener breakdown voltage is 15 V) [3]

Solution:
By heavy dope zener diode we get the weak deplation layer.
\(\mathrm{I}=\frac{20}{1250}=\frac{2}{125}\)
Voltage at 10 kΩ resistor will be
\(\mathrm{V}=\frac{2}{125} \times 1000=16\) volt
zener diode behave as plane wire so as \(\mathrm{I}=\frac{\mathrm{V}}{\mathrm{R}}=\frac{20}{250}=\frac{2}{25} \mathrm{A}\)

Question 15.
Draw a labelled diagram of cyclotron. Explain its working principle. Show that cyclotron frequency is independent of the speed and radius of the orbit. [3]
OR
(a) Derive, with the help of a diagram, the expression for the magnetic field inside a very long solenoid having n turns per unit length carrying a current I.
(b) How is a toroid different from a solenoid?
Solution:

Principle: the frequency of charge particle moving in magnetic field is independent of its speed.

OR

Question 16.
Prove that the magnetic moment of the electron revolving around a nucleus in an orbit of radius r with orbital speed v is equal to evr/2. Hence using Bohr’s postulate of quantization of angular momentum, deduce the expression for the magnetic moment of hydrogen atom in the ground state. [3]
Solution:

Question 17.
Two large charged plane sheets of charge densities σ and –2σ C/m2 are arranged vertically with a separation of d between them. Deduce expressions for the electric field at points [3]
(i) to the left of the first sheet
(ii) to the right of the second sheet, and
(iii) between the two sheets.
OR
A spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. Find out the surface charge density on the inner and outer surfaces of the shell.
(b) Is the electric field inside a cavity (with no charge) zero; independent of the fact whether the shell is spherical or not? Eplain.
Solution:

OR

(b) inside the cavity without any charge net electric field is always zero according to gauss law.

Question 18.
A signal of low frequency fm is to be transmitted using a carrier wave of frequency fc. Derive the expression for the amplitude modulated wave and deduce expressions for the lower and upper sidebands produced. Hence, obtain the expression for modulation index. [3]
Solution:

Question 19.
Draw a plot of α-particle scattering by a thin foil of gold to show the variation of the number of the scattered particles with scattering angle. Describe briefly how the large angle scattering explains the existence of the nucleus inside the atom. Explain with the help of impact parameter picture, how Rutherford scattering serves a powerful way to determine an upper limit on the size of the nucleus. [3]
Solution:

Large angle scattering of α-particles is possible only when it must have a collision with a very particle which
is confine in a very small region as the number of particles scattering at large angles were also very less. This
leads the discovery of nucleus inside the atom.
Since small the impart parameter will deflect the particle by large amount since only few of the α-particle
deflects by large angle this concludes that for most of the α-particle impact parameter is large thus size of the
nucleus is very small.

Question 20.
A 200 μF parallel plate capacitor having plate separation of 5 mm is charged by a 100 V dc source. It remains connected to the source. Using an insulated handle, the distance between the plates is doubled and a dielectric slab of thickness 5 mm and dielectric constant 10 is introduced between the plates. Explain with reason, how the (i) capacitance, (ii) electric field between the plates, (iii) energy density of the capacitor will change? [3]
Solution:

Question 21.
Why is it difficult to detect the presence of an anti-neutrino during β-decay? Define the term decay constant of a radioactive nucleus and derive the expression for its mean life in terms of the decay constant. [3]
OR
(a) State two distinguishing features of nuclear force.
(b) Draw a plot showing the variation of potential energy of a pair of nucleons as a function of their separation. Mark the regions on the graph where the force is
(i) attractive, and
(ii) repulsive.
Solution:
Since neutrino and antinutrino are very small particles which rarely intracts with the matter thus its very difficult to detect them.
Decay constant ⇒ It is the reciprocal of that time in which N0 of active nuclei reduces to 37% of initial active nuclei.

OR

Question 22.
A triangular prism of refracting angle 60º is made of a transparent material of refractive index 2/ 3 . A ray
of light is incident normally on the face KL as shown in the figure. Trace the path of the ray as it passes
through the prism and calculate the angle of emergence and angle of deviation. [3]

Solution:

Question 23.
Prove that in a common-emitter amplifier, the output and input differ in phase by 180º.
In a transistor, the change of base current by 30 mA produces change of 0.02 V in the base-emitter voltage
and a change of 4 μA in the collector current. Calculate the current amplification factor and the load
resistance used, if the voltage gain of the amplifier is 400. [3]
Solution:

V_CE = V_CC– I_CR_L
When i_B increase as in first half cycle the i_C will also increase as well as the V_CE = –ve this negative sign
show the cycle is at phase 180º.

Question 24.
Show, on a plot, variation of resistivity of
(i) a conductor, and
(ii) a typical semiconductor as a function of temperature.
Using the expression for the resistivity in terms of number density and relaxation time between the collisions, explain how resistivity in the case of a conductor increases while it decreases in a semiconductor, with the rise of temperature. [3]
Solution:


in conductors the collision of e^– will be increases &  in semi-conductors the new e^– holes pair creates & conductivity increases.

SECTION D

Question 25.
(a) Derive an expression for the induced emf developed when a coil of N turns, and area of cross-section A, is rotated at a constant angular speed ω in a uniform magnetic field B.
(b) A wheel with 100 metallic spokes each 0.5 m long is rotated with a speed of 120 rev/min in a plane ormal to the horizontal component of the Earth’s magnetic field. If the resultant magnetic field at that place is 4 × 10^-4 T and the angle of dip at the place is 30º, find the emf induced between the axle and the rim of the wheel. [5]
OR
(a) Dervie the expression for the magnetic energy stored in an inductor when a current I develops in it. Hence, obtain the expression for the magnetic energy density.
(b) A square loop of sides 5 cm carrying a current of 0.2 A in the clockwise direction is placed at a distance of 10 cm from an infinitely long wire carrying a current of 1 A as shown. Calculate
(i) the resultant magnetic force, and
(ii) the torque, if any, acting on the loop.

Solution:

OR

Question 26.
Explain, with the help of a diagram, how plane polarized light can be produced by scattering of light from the Sun.
Two polaroids P₁ and P₂ are placed with their pass axes perpendicular to each other. Unpolarised light of intensity I is incident on P₁. A third Polaroid P₃ is kept between P₁ and P₂ such that its pass axis makes an angle of 45º with that of P₁. Calculate the intensity of light transmitted through P₁, P2 and P3. [5]
OR
(a) Why cannot the phenomenon of interference be observed by illuminating two pin holes with two sodium lamps?
(b) Two monochromatic waves having displacements y₁ = a cos ωt and y₂ = a cos (ωt + φ) from two coherent sources interfere to produce an interference pattern. Derive the expression for the resultant intensity and obtain the conditions for constructive and destructive interference.
(c) Two wavelengths of sodium light of 590 nm and 596 nm are used in turn to study the diffraction taking place at a single slit of aperture 2 × 10^–6 m. If the distance between the slit and the screen is 1.5 m, calculate the separation between the positions of the second maxima of diffraction pattern obtained in the two cases
Solution:

if object size around wavelength of light get scattered & at 90º placed observer get the polarised light due to
all vibration of light used for oscillating molecules except perpendicular

OR
(a) Two lamps not a coherent source that why their phase difference not constant with time.
(b) y = y₁ + y₂
y = acos(ωt) + a cos (ωt + Φ)
y = a.cos(ωt) + a[cos(ωt).cosΦ – sin(ωt) sinΦ]
y = a.cos(ωt) + a.cos(ωt).cosΦ – a.sin(ωt) sinΦ
y = (a + a.cosφ).cos(ωt) – a.sinφ.sin(ωt)
a + a cos φ = R.sinθ …(i)
–asinφ = R.cosθ …(ii)
y = R.sinθ.cos(ωt) + R.cosθ.sin(ωt)
y = Rsin(ωt + θ)
(i)² + (ii)²(a + a.cosΦ)² + (–asinΦ)² = R²a² + a².cos²Φ + 2a²cosΦ + a2sin²φ = R²a² + a² + 2a².cosΦ = R2R² = 2a² + 2a².cosΦR² = 2a²(1 + cosΦ)
R² = 2a²(1 + \(2 \cos ^{2} \frac{\phi}{2}-1\))
\(\begin{array}{l}{\mathrm{R}^{2}=4 \mathrm{a}^{2} \cdot \cos ^{2} \frac{\phi}{2}} \\ {\mathrm{I}_{\mathrm{Net}}=4 \cdot \mathrm{I}_{0} \cdot \cos ^{2} \frac{\phi}{2}}\end{array}\)
constructive Φ = 0, 2π, 4π ….
I_Net = 4I₀.cos²(0º)
I_Net = 4I₀.
Destructive Φ = π, 3π, 5π
\(\mathrm{I}_{\mathrm{Net}}=4 \mathrm{I}_{0} \cos ^{2}\left(\frac{\pi}{2}\right)\)
I_Net = 0

Question 27.
(a) Describe briefly, with the help of a circuit diagram, the method of measuring the internal resistance of a cell.
(b) Give reason why a potentiometer is preferred over a voltmeter for the measurement of emf of a cell.
(c) In the potentiometer circuit given below, calculate the balancing length l. Give reason, whether the circuit will work, if the driver cell of emf 5V is replaced with a cell of 2 V, keeping all other factors constant. [5]

OR
(a) State the working principle of a meter bridge used to measure an unknown resistance.
(b) Give reason
(i) why the connections between the resistors in a metre bridge are made of thick copper strips.
(ii) why is it generally preferred to obtain the balance length near the mid-point of the bridge wire.
(c) Calculate the potential difference across the 4 Ω resistor in the given electrical circuit, using Kirchhoff’s rules.

Solution:

(b) Potentiometer work on no current flow method but voltmeter work on current flow through voltmeter so emf cannot drawn by using voltmeter.


So, the circuit will not work due to balancing length is greater than original length of wire.
OR
(a) meter bridge work on the principle of wheat stone bridge
(b) (i) because thick wire has low resistance which can not alter the value of unknown resistance
(ii) If balance length become at mid point so that R = S
\(\frac{\mathrm{R}}{\ell}=\frac{\mathrm{S}}{(100-\ell)}\)
Unknown resistance become equal to standard resistance.