Algebra Class 6 Extra Questions Maths Chapter 11
Extra Questions for Class 6 Maths Chapter 11 Algebra
Algebra Class 6 Extra Questions Very Short Answer Type
Question 1.
Six less than a number equals to two. What is the number?
Solution:
Let the number be ‘x’.
According to condition, we have x – 6 = 2
By inspections, we have 8 – 6 = 2
∴ x = 8
Thus, the required number is 8.
Question 2.
Write an algebraic expression for each of the following:
(a) 3 subtracted from a number y.
(b) 5 is added to three times a number x.
Solution:
(a) The required expression is y – 3
(b) The required expression is 5 + 3x
Question 3.
Write an algebraic expression for the following expressions:
(a) The sum of a number x and 4 is doubled.
(b) One fourth of a number x is added to one third of the same number.
Solution:
(a) The required expression is 2 x (x + 4)
(b) The required expression is \(\frac { 1 }{ 4 }\)x + \(\frac { 1 }{ 3 }\)x
Question 4.
Think of a number x. Multiply it by 3 and add 5 to the product and subtract y subsequently. Find the resulting number.
Solution:
Required number is (3x + 5)
Now we have to subtract y from the result i.e., 3x + 5 – y
Question 5.
Here is a pattern of houses with matchsticks:
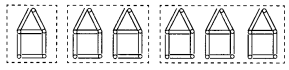
Write the general rule for this pattern.
Solution:
One house is made of 6 matchsticks i.e. 6 x 1
Two houses are made of 12 matchsticks i.e. 6 x 2
Three houses are made of 18 matchsticks i.e. 6 x 3
∴ Rule is 6n where n represents the number of houses.
Question 6.
If the side of an equilateral triangle is x, find its perimeter.
Solution:
We know that the three sides of an equilateral triangle are equal.
∴ x + x + x = 3x.
Thus, the required perimeter = 3x units.
Question 7.
If x = 3, find the value of the following:
(i) x + 5
(ii) 2x – 3
(iii) x – 7
(iv) \(\frac { x }{ 3 }\) – 1
Solution:
Given that x = 3
(i)x + 5 = 3 + 5 = 8
(ii) 2x – 3 = 2 x 3 – 3 = 6 – 3 = 3
(iii) x – 7 = 3- 7 = -4
(iv) \(\frac { x }{ 3 }\) – 1 = \(\frac { 3 }{ 3 }\) -1 = 1 – 1 = 0
Question 8.
If x = 2, y = 3 and 2 = 5, find the value of;
(a) 2x + y + z
(b) 4x -y + z
(c) x – y + z
Solution:
(a) Given that: x – 2, y = 3 and z = 5
∴ 2x + y + 2 = 2 x 2 + 3 + 5
= 4 + 3 + 5 = 12
(b) 4x – y + z = 4 x 2 – 3 + 5
= 8 – 3 + 5 = 5 + 5 = 10
(c) x – y + z = 2 – 3 + 5 = -1 + 5 = 4
Question 9.
State which of the following are equations with a variable?
(a) 12 = x – 5
(b) 2x > 7
(c) \(\frac { x }{ 2 }\) = 5
(d) 5 + 7 = 3 + 9
(e) 7 = (11 x 5) – (12 x 4)
Solution:
(a) 12 = x – 5 is an equation with a variable x.
(b) 2x > 7 is not an equation because it does not have ‘=’ sign.
(c) \(\frac { x }{ 2 }\) = 5 is an equation with a variable x.
(d) 5 + 7 = 3 + 9 is not an equation because it has no variable.
(e) 7 = (11 x 5) – (12 x 4) is not an equation because it has no variable.
Question 10.
Think of a number, add 2 to it and then multiply the sum by 6, the result is 42.
Solution:
Let the number be x.
∴ Sum of x and 2 = x + 2
Now by multiplying the sum by 6, we get
6 × (x + 2) = 42
⇒ 6 × x + 6 × 2 = 42
⇒ 6x + 12 = 42
By inspection, we get
6 × 5 + 12 = 42
⇒ 30 + 12 = 42
∴ 42 = 42
So, the required number = 5
Algebra Class 6 Extra Questions Short Answer Type
Question 11.
The side of a regular hexagon is s cm. Find its perimeter.
Solution:
Each side of a regular hexagon = s
∴ its perimeter = s + s + s + s + s + s = 6s cm

Question 12.
If a = 3, b = \(\frac { 1 }{ 2 }\) and c = \(\frac { 1 }{ 4 }\), find the value of

Solution:

Question 13.
Complete the table and find the solution of the equation 19 – x = 13

Solution:
By inspection, we have

Thus, the required solution is 6.
Question 14.
If x = –\(\frac { 1 }{ 2 }\), y = \(\frac { 1 }{ 4 }\) and z = 0, find the value of the given expressions
(a) 8z + 2x -y
(b) z – y + 3x
Solution:

Question 15.
Fill in the blanks:
(a) 5 added to -5 = ……….
(b) If x = 3, then 3x – 5 = ……….
(c) If x = 1 and y = 2, then 2x + 3y = ……….
(d) If 10x – 6 = 14, then x = ……….
(e) 4 less than a number x = ……….
Solution:
(a) 0
(b) 4
(c) 8
(d) 2
(e) x – 4
Algebra Class 6 Extra Questions Higher Order Thinking Skills (HOTS)
Question 16.
A starts his car from Delhi at 6.00 am to Amritsar. The uniform speed of his car is x km/h. At 12.00 noon, he finds that he is still 50 km away from Amritsar. Find the distance between Delhi and Amritsar.
Solution:
Time taken by A to reach Amritsar = 12.00 noon – 6.00 am = 6 hour.
The uniform speed of the car = x km/ hr
∴ Total distance covered by A = Time x speed = 6x km.
∴ Distance between Delhi and Amritsar = (6x + 50) km.
Question 17.
Anshika’s Score in Science is 15 more than the two-third of her score in Sanskrit. If she scores x marks in Sanskrit, find her score in Science.
Solution:
Anshika’s score in Sanskrit = x
∴ Her marks in Science = \(\frac { 2 }{ 3 }\)x +15
∴ Thus, Anshika’s score in Science = \(\frac { 2 }{ 3 }\)x + 15